Эксперименты и теоретические исследования показывают, что размер частицы является активной переменной, определяющей вместе с другими термодинамическими параметрами состояние системы.
Принято различать два типа размерных эффектов [1]: собственный, или внутренний, и внешний. Внутренний размерный эффект связан со специфическими изменениями в объемных и поверхностных свойствах как индивидуальных частиц, так и получаемых в результате их самоорганизации ансамблей. Внешний эффект является размерно зависимым ответом на внешнее поле, не зависимым от внутреннего эффекта.
Внешние размерные эффекты в твердых телах возникают тогда, когда геометрический размер их становится сравним с одним из параметров, характеризующих движение квазичастиц (волна де Бройля, длина свободного пробега и др.). Размерные эффекты проявляются в зависимости кинетических коэффициентов электропроводности, теплопроводности и др. от размера образца при наложении внешнего поля (электрического, магнитного и т.д.).
Размерным эффектам в твердых телах посвящено большое количество работ (см., например [1, 2]). В настоящей работе мы рассмотрим размерные эффекты в минералах и их анализ на основе развитого нами термодинамического подхода [3, 4].
Надо отметить, что исследования размерных эффектов в минералах непосредственно связаны с возникновением нового направления в минералогии – наноминералогии [5–7]. При этом наноминералы рассматриваются как продукт природных нанотехнологий, происходящих в наномасштабе.
Неравновесная термодинамика элементарных возбуждений в твердых телах
Подсистему магнитных, электрических диполей, дефектов и других элементарных возбуждений в твердом теле (минерале) или поверхностном слое (дислокации, поры и т.д.) будем рассматривать как систему невзаимодействующих частиц, погруженную в термостат. Квантовые переходы, обусловленные взаимодействием дефектов с термостатом, будут диссипативными (с вероятностью Р) в отличие от взаимодействия с внешним полем (с вероятностью F). Диссипативные процессы приводят к тому, что вторичное поле (отклик системы) всегда меньше первичного, вызывающего образование дефектов.
Поскольку подсистема дефектов обменивается с термостатом только энергией, то соответствующий им ансамбль частиц будет каноническим. В этом случае выражение для статистической энтропии имеет вид:
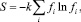 (1)
(1)
где fi – функция распределения; k – постоянная Больцмана.
Дифференцируя (1) по времени и преобразуя, получим:
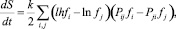 (2)
(2)
где Pij – вероятность перехода из начального i (с энергией Ei) в возбужденное состояние j (с энергией Ej).
Для диссипативных процессов принцип детального равновесия имеет вид:
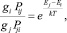 (3)
(3)
где gi, gj – статистические веса для уровней Ei и Ej.
Опуская промежуточные вычисления (подробнее см. в [8]), получим:
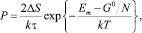 (4)
(4)
где ΔS – изменение энтропии в диссипативном процессе; Em – среднее значение энергии основного состояния дефектов; τ – время релаксации.
Для функции отклика Ф системы на внешнее поле имеем:
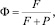 (5)
(5)
где Р – вероятность диссипативного процесса и определяется (4); F определяет вероятность перехода в возбужденное состояние за счет первичного внешнего поля, причем F = 1/τр, где τр – время жизни возбужденного состояния. С учетом (4) выражение (5) примет вид:
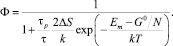 (6)
(6)
Размерные эффекты в магнитных свойствах минералов
Вопросы магнетизма малых ферромагнитных частиц исследуются уже давно [9]. Важность учета размера зерен ферромагнитных минералов в геофизических исследованиях подчеркивалась в работах [10–12]. В настоящее время эти вопросы не потеряли актуальность. Основным механизмом, приводящим к зависимости магнитной восприимчивости от размера частиц ферромагнетика считается переход многодоменных частиц в однодоменные. Критический размер (радиус d) однодоменной частицы, выше которого она становится двух- или многодоменной, определяется из энергетических соображений и обратно пропорциональна квадрату намагниченности насыщения Js [9]:
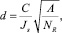 (7)
(7)
где С = 0,5; 1; 2 для простой кубической, объемоцентрированной и гранецентрированной решетки, соответственно; А – параметр обменной энергии; NR – размагничивающий фактор вдоль малой оси частицы.
В случае больших энергий анизотропии вместо (7) используется формула [10-11]:
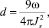 (8)
(8)
где w – плотность поверхностной энергии доменов.
Беря в качестве функции отклика в (6) магнитную восприимчивость и приводя (6) к линейному виду, получим:
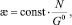 (9)
(9)
где N – число магнитных диполей; G0 – термодинамический потенциал Гиббса ферромагнетика.
Изменение радиуса зерна ферромагнетика также приводит к изменению давления Р на межфазной границе, описываемое уравнением Кельвина
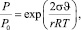 (10)
(10)
где r – радиус зерна; s – межфазное поверхностное натяжение; ϑ – молярный объем; P0 – давление над плоской поверхностью; R – газовая постоянная.
Поскольку 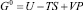 , то вдали от точки Кюри из соотношений (9) и (10) следует
, то вдали от точки Кюри из соотношений (9) и (10) следует
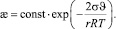 (11)
(11)
Разлагая экспоненту в ряд и ограничиваясь первыми двумя членами, получим:
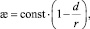 (12)
(12)
где 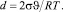 (13)
(13)
Удельная намагниченность магнетитов Соколовского, Сарбайского месторождений исследовалась нами на вибрационном магнитометре. Размер зерна магнетита определялся на микроскопе МИМ-8. Результаты показаны на рис. 1. В координатах æ/æ0 ~ 1/r экспериментальная кривая спрямляется в соответствии с (12), давая значение d = 0,36 мкм.
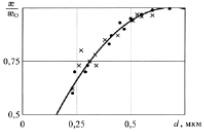
Рис. 1. Зависимость относительной магнитной восприимчивости от диаметра зерна магнетита
Для магнетита ϑ = 44,5 см3/моль, и из соотношения (8) для поверхностного натяжения s получаем: s = 10,07⋅103 эрг/см2. Расчет плотности поверхностной энергии для магнетита [9] по формуле (8) (Js = 4,9∙105 А/м дает w = 10,1⋅103 эрг/см2, что совпадает с полученной нами величиной s.
Экспериментальное определение поверхностного натяжения твердых тел затруднено тем, что их молекулы (атомы) лишены возможности свободно перемещаться. Исключение составляет пластическое течение металлов при температурах, близких к точке плавления [13].
Как следует из приведенных выше результатов, поверхностное натяжение магнитных материалов экспериментально можно определять по зависимости æ = æ(r) и по формуле (13). Рассмотренный выше размерный эффект относится к внешним размерным эффектам.
Температура плавления наночастиц
Изменение температуры плавления металлов в зависимости от размера частиц относится к внутреннему размерному эффекту. С уменьшением размера частиц температура плавления может изменяться на несколько сотен градусов и больше.
Зависимость температуры плавления от размера частиц рассматривается на основе двух моделей: одна из них использует представления термодинамики [14], другая – колебания атомов [15]. Подробное рассмотрение термодинамического подхода приведено в обзоре [16].
Экспериментальная кривая зависимости температуры плавления частиц золота от их размера и приведенная в работе [14], с большой точностью описывается уравнением, подобным (12):
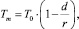 (14)
(14)
где Т0 – температура плавления массивного образца, d определяется (13).
При температуре Т = 1040 °С величина поверхностного натяжения золота, вычисленная по нашей формуле (13), оказалась равной: s = 1,312 Дж/м2. Эта величина незначительно отличается от величины поверхностного натяжения, полученной в методе «нулевой ползучести» s = (1,37 ± 0,15) Дж/м2 [17].
В работе [18] для нанокристаллов алюминия получена экспериментальная кривая, аналогичная кривой работы [14] для золота. Расчет величины поверхностного натяжения по нашей формуле дал следующий результат: s = 1,070 Дж/м2, что также близко к значению s = (1,14 ± 0,2) Дж/м2 для алюминия, полученного в методе «нулевой ползучести».
Размерные эффекты, электрические и теплофизические свойства минералов
Если воспользоваться аналогией потенциальных скалярных полей (см., например, [19]), то нетрудно получить:
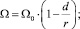 (15)
(15)
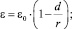 (16)
(16)
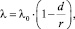 (17)
(17)
где Ω – электропроводность; ε – диэлектрическая проницаемость; λ – коэффициент теплопроводности малых частиц минерала. Здесь d определяется соотношением (13).
Обобщенная зависимость физического свойства минерала от его размера показана на рис. 2.
Во всех случаях экспериментальное определение зависимости физического свойства минералов от его размеров позволяет определить поверхностное натяжение минерала. Последнее играет важную роль в процессах переработки минерального сырья – измельчение при рудоподготовке (работа диспергирования А = σ·S, S – площадь поверхности частицы); в процессах обогащения – флотация, магнитная сепарация и т.д.; в процессах металлургического передела и многих других [20–23].
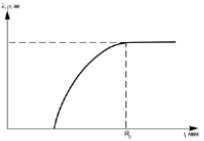
Рис. 2. Обобщенная зависимость физического свойства минерала от его размера
Заключение
Из приведенных выше результатов нашего исследования следует, что размерные эффекты (и внутренний и внешний) описываются одной универсальной зависимостью:
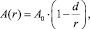
где A(r) – физическое свойство частицы минерала радиусом r; А0 – физическое свойство массивного образца. Во всех случаях d определяется соотношением (13).
Фундаментальная причина такой универсальной зависимости пока не ясна и требует дальнейших исследований.
Библиографическая ссылка
Портнов В.С., Юров В.М., Исагулов А.З., Сергеев В.Я., Орынгожина С.Е. Размерные эффекты и физические свойства минералов // Современные наукоемкие технологии. 2013. № 4. С. 85-88;URL: https://top-technologies.ru/ru/article/view?id=31613 (дата обращения: 11.12.2025).



