Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Портнов В.С. 1 Юров В.М. 2 Исагулов А.З. 1 Турсунбаева А.К. 1 Когай Г.Д. 1 Камаров Р.К. 1

---

1 Карагандинский государственный технический университет

2 Карагандинский государственный университет им. Е.А. Букетова

Рассмотрены вопросы использования термодинамики, теории информации и метода аналогий к анализу свойств минералов, которые представляют собой гетерогенные системы. На основе неравновесной статистической термодинамики получена формула для электрической проводимости гетерогенных сред. На основе метода аналогий получено соотношение для коэффициента теплопроводности минералов. Используя теорию информации, получена формула для магнитной восприимчивости магнитных минералов. Полученные формулы хорошо согласуются с экспериментальными данными. Результаты работы могут быть использованы при анализе геофизических данных.

Статья в формате PDF

723 KB

термодинамика

информация

метод аналогий

свойства минералов

1. Поплавский Р.П. Термодинамика информационных процессов. – М: Наука, 1981. – 255 с.

2. Хакен Г. Информация и самоорганизация. – М.: Мир, 1991. – 240 с.

3. Гиббс Дж.В. Термодинамика. Статистическая механика: Избранные труды. – М.: Наука, 1982. – 584 c.

4. Шеннон К. Работы по теории информации и кибернетике. – М.: ИЛ, 1963. – 829 c.

5. Хинчин А.Я. Понятие энтропии в теории вероятностей // УМН. – 1953. – Т.8. – Вып. 3. – С. 3–20.

6. Мидлтон Д. Статистическая теория обнаружения сигналов // Прием сигналов при наличии шума. – М.: ИЛ, 1960. – С. 25–56.

7. Колмогоров А.Н. Теория передачи информации // Известия АН СССР. – 1957. – С. 66–99.

8. Колмогоров А.Н.. Три подхода к определению понятия количества информации // Проблемы передачи информации. – 1965. – Вып. 1. – Т.1. – С. 3–34.

9. Хартли Р. Передача информации // Теория информации и ее приложенияю. – М.: Физматгиз, 1959. – С. 56–134.

10. Бинс К., Лауренсон П. Анализ и расчет электрических и магнитных полей. – М.: Энергия, 1970. – 376 с.

11. Портнов В.С., Юров В.М. Связь магнитной восприимчивости магнетитовых руд с термодинамическими параметрами и содержанием железа // Известия вузов. Горный журнал. – 2004. – № 6. – С. 122–127.

12. Портнов В.С. Термодинамический подход к задачам геофизического опробования железорудных месторождений. – Караганда: КГТУ, 2003. – 212 с.

13. Яворский В.В., Юров В.М. Прикладные задачи термодинамического анализа неравновесных систем. – М.: Энергоатомиздат, 2008. – 338 с.

Особое значение в последние годы уделяется внимание термодинамике различных процессов, как в естественных, так и гуманитарных науках, включая социологию, психологию, мышление, учебный процесс и многое другое. При этом, определяющую роль играет понятие энтропии, тесно связанное с понятием информации.

Помимо разнообразия формулировок понятия энтропии разнообразны и примеры ее применения. Идеология всех таких приложений связана с экстремальными принципами естествознания – возрастающее значение энтропии параметризует изменение состояния систем самой различной природы в процессе их «естественной» эволюции. Соответствующий принцип развития получил название «принцип максимума энтропии». Для закрытых термодинамических систем их энтропия возрастает («второе начало» термодинамики).

На начальном этапе развития теории информации существовало мнение, что малая энергоемкость информационных процессов существенно отличает их от энергетических. С развитием и усложнением информационных систем встал вопрос и об определении энергетической сложности различных информационных процессов, выяснения предельных соотношений при получении, хранении и обработке информации. Это послужило основой для известного высказывания фон Неймана: «…термодинамика является той частью теоретической физики, которая в некоторых из своих аспектов наиболее близка теории обработки и измерения информации…». Таким образом, потребности техники и развитие науки привели к возникновению термодинамики информационных процессов, основы которой были заложены в 1956 г. Бриллюэном. Однако существенного внимания со стороны исследователей вопросы термодинамики информационных процессов не получили.

Исключение составляют основополагающие работы Р.П. Поплавского [1]. Им было подчеркнуто, что термодинамика информационных процессов, в отличие от равновесной термодинамики и термодинамики открытых систем, является термодинамикой переходных процессов. Им было также установлены предельные соотношения между информационными характеристиками (точность, количество информации) и термодинамическими (энергия, энтропия).

80–90-е годы ХХ века стали временем бурного развития (и в настоящее время) синергетики, основу которой составляет термодинамика отрытых систем, в связи с выявлением глубокой связи между информацией и самоорганизацией материи [2].

Энтропия и информация

Энтропия термодинамической системы 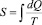(где Q – полученная системой от среды теплота, а Т – температура процесса) была введена в 1865 г. Рудольфом Клаузиусом. В 1872 г. Людвиг Больцман вводит статистическую энтропию S = klnW (здесь W – вероятность макросостояния, отождествляемая с числом микросостояний системы при условии их равновероятности, а k – коэффициент пропорциональности, зависящий от принятой размерности энтропии.). Дж.В. Гиббс [3] для статистического обоснования термодинамики вводит в 1902 г. вероятностные представления:

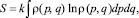(1)

здесь p(p,q) – плотность вероятности распределения обобщенных координат q и импульсов р в фазовом пространстве системы; k – размерный множитель. В 1948 г. Клод Шеннон [4] предложил формулу для оценки неопределенности кодовой информации в каналах связи, называемую энтропией Шеннона:

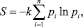
где pi – вероятность встречаемости символа i в коде, содержащем N символов; k – размерный множитель. В 1953 г. появляется работа А.Я. Хинчина [5], где формула Шеннона аксиоматически применяется для описания неопределенности схем в теории вероятности. В работах Роберта Мак Артура в 1955г. аналог формулы Шеннона появился как мера биологического разнообразия экологических сообществ:

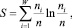
где ni – численность i-й популяции в сообществе из W видов [6].

А.Н. Колмогоров с коллегами в 1956 г. [7] развили вероятностное определение энтропии 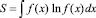для приложения к теории информации (f(x) здесь функция распределения случайной величины х). В 1958 г. А.Н. Колмогоров [8] ввел для динамических систем метрическую энтропию, или К-энтропию, которая пропорциональна скорости изменения статистической энтропии Больцмана. До настоящего момента продолжают появляться обобщения энтропийных формул. Так, в 2000 г. А.В. Коганов обобщил статистическое определение комбинаторной энтропии – логарифм числа состояний системы – на понятие математической модели.

В основе всей теории информации лежит открытие, заключающееся в том, что информация допускает количественную оценку. Наиболее четко, вплоть до введения количественной меры информации, эта мысль, по-видимому, впервые была высказана Хартли в 1928 г. [9], а затем, уже на более высоком уровне, развита и обобщена Шэнноном, Винером, фон Нейманом, Фишером, Колмогоровым и другими.

Для развития теории информации в ее современном виде вообще не требуется определения понятия информации как таковой; необходимым и достаточным для построения теории является понятие количества информации. Поэтому употребление терминов «информация» и «количество информации» как синонимов не вызывает недоразумений в рамках самой теории.

Метод аналогий и поля-аналоги

Тенденция возникновения интегрирующих научных направлений на стыке уже устоявшихся наук, возникла достаточно давно. Междисциплинарный подход в современном естествознании всегда имеет место для решения научных проблем.

Cуществуют чрезвычайно простые и универсальные законы функционирования и развития физического мира. Выявление таких законов позволит создать метод для осуществления интеграции науки. В настоящее время таким методом является метод аналогий. Примером его успешного использования являются работы Дж. Максвелла при создании классической теории электромагнетизма. В знаменитых лекциях по физике Р. Фейнмана 7-й том посвящен электростатическим аналогиям. В табл. 1 показана аналогия, существующая между величинами в различных скалярных потенциальных полях [10].

Электрические свойства минералов

Рассмотрим сначала гомогенную изотропную среду, которая содержит 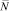электронов проводимости и характеризуется термодинамическим потенциалом Гиббса G° Возникновение тока плотностью j в среде является откликом системы невзаимодействующих электронов на внешнее поле и имеет вид [11]:

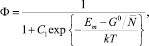(2)

где 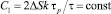(смысл входящих в это выражение величин такой же, как и в [11]); е – заряд электрона.

Таблица 1

Аналогия между величинами в потенциальных полях [10]

После линеаризации (2) при Φ = j, получаем:

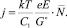(3)

Когда 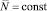, мы из (3) имеем закон Ома в дифференциальной форме:

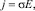(4)

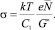где (5)

Проводимость s связана с удельным сопротивлением r соотношением

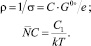(6)

Константа С характеризует процесс перехода системы электронов из возбужденного состояния в основное и примерно одинакова для многих веществ. Исключение могут составлять только те вещества, где реализуются специфические механизмы рассеяния. Таким образом, гетерогенность среды будет сказываться на ее электропроводности через энергию Гиббса G°, которая известна для большинства минералов.

Теплофизические свойства минералов

Используя метод аналогий (табл. 1) для коэффициента теплопроводности минералов нами получено уравнение:

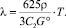(7)

В уравнение (7) входят только два параметра минерала – плотность и энергия Гиббса, которые экспериментально определены для большого количества минералов и представлены в справочниках. Для коэффициента мы получили значение С2 = 2,8·10–2 м2/кг∙с). В табл. 2 приводятся экспериментальные значения коэффициента теплопроводности и вычисленные по формуле (7).

Таблица 2

Сравнение экспериментальных и теоретических значений коэффициента теплопроводности некоторых минералов

Из табл. 2 видно, что экспериментальные и теоретические значения хорошо согласуются друг с другом. Это, на наш взгляд, неплохой результат и подтверждает основные положения нашей модели.

Энтропия и магнитные свойства минералов

Наложение внешнего магнитного поля на систему магнитных диполей, погруженную в термостат, приводит к изменению ее энтропии:

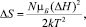(8)

где μБ = 9,27 10–27 Дж∙Тл–1 – магнетон Бора; Н – напряженность внешнего магнитного поля; N – число магнитных диполей.

После несложных преобразований мы получим:

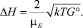(9)

Если считать, что искомый полезный компонент связан только с одним магнитным диполем, то его концентрацию сп можно найти из соотношения N = NA∙cп/100 %, где NA – число Авогадро.

Используя выше приведенные формулы, получим:

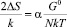(10)

или

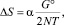
где α = const.

Изменение энтропии объекта обратно пропорционально количеству ΔI информации о нем, т.е.:

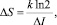(11)

где kln 2 – энергетический эквивалент информации.

С другой стороны, информацию о магнитных свойствах объекта несет его магнитная восприимчивость χ, т.е.:

ΔI = χ. (12)

С учетом (10) и (11) для магнитной восприимчивости имеем:

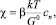(13)

где β – некоторая постоянная.

Уравнение (13) совпадает с уравнением, полученного нами в работе [11], с использованием подхода, основанного на функции отклика системы магнитных диполей. Из уравнения (13) следует линейная зависимость магнитной восприимчивости от концентрации магнитной компоненты минерала (рисунок).

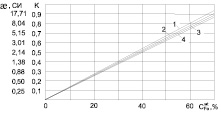
Зависимость магнитной восприимчивости и коэффициента отображения от содержания магнетитового железа:1 – Кентобинское, 2 – Сарбайское, 3 – Куржункульское, 4 – Соколовское месторождения

Видно, что экспериментальные данные хорошо ложатся на теоретические прямые.

Заключение

Мы изложили фрагментарно основные идеи использования термодинамического подхода, теории информации и метода аналогий к задачам минералогии. Некоторые затронутые вопросы рассматривались нами в работах [12, 13] в рамках неравновесной статистической термодинамики.

Библиографическая ссылка