В процессе трения поверхностные слои материалов переходят в специфическое состояние, которое характеризуется как фазово-разупорядоченное по отношению к исходному состоянию [1–3]. Методики анализа фазовой и структурной разупорядоченности поверхности антифрикционных материалов и композиционных покрытий (КП), представлена в работах [4–7].
Наличие межфазных «дефектов» является прямым следствием фазово-разупорядоченного состояния, особенно компонентов системы в ультрадисперсном состоянии [8–10]. В этом случае может проявляться эффект синергизма – отклонение свойства материала от величины, которая может быть получена по аддитивной схеме с учетом индивидуальных характеристик фаз. В соответствии с синергической моделью «концентрационной волны» [10] трибологические свойства (скорость линейного износа или коэффициент трения) КП зависят также от относительной величины эффекта синергизма, который определяется параметрами k и kн – размерным и наноструктурным факторами, соответственно. Экспериментально установлено [11–17], что для КП разного фазового состава параметр kн принимает значения в интервале от 0,03 до 0,17 и характеризует объемную долю наночастиц фаз твердых компонент трибосопряженных поверхностей. Одновременный учет вероятного синергизма свойств компонентов КП и анализ возможного фазово-разупорядоченного состояния трибосопряженных поверхностей позволил осуществить целенаправленный выбор эффективных модификаторов для КП на основе никельсодержащих систем [18]. Теоретическим обоснованием для этого послужили методы символьного описания модульного строения компонентов КП и методы модулярного дизайна наноструктур [19–29].
Данная работа посвящена анализу возможной структурно-фазовой разупорядоченности углеродсодержащих наночастиц в антифрикционных КП, модифицированных наноалмазом. Рассмотрены некоторые из вероятных наноструктур с гомоатомными оболочками пентагональной ветви классификации фуллеренов, предложенной в [30].
Можно предположить, что в процессе трения КП, модифицированного наноалмазом, происходит разрушение агрегатов углеродсодержащих наночастиц, «графитизация» их поверхностных оболочек и образование, в частности, «ядер» в виде фуллереноподобных наноструктур состава Cn с n ≥ 20. Пентагональный додекаэдр характеризует форму малого фуллерена C20, на основе которого могут быть сконструированы икосаэдрические наноалмазы с тетраэдрической sp3-координацией атомов углерода, и онионы – многослойные фуллереноподобные частицы с sp2-координацией атомов углерода.
В качестве допустимых топологических преобразований пентагондодекаэдра будем рассматривать сплитинг-преобразование узлов и стеллейшн-дизайн граней. Основная цепочка топологических преобразований (см. рис. 1):
пентагондодекаэдр PD{555} → усеченный пентагондодекаэдр tPD{3.10.10} → икосододекаэдр ID{3535} → усеченный икосаэдр tI{566} → икосаэдр I{33333}.
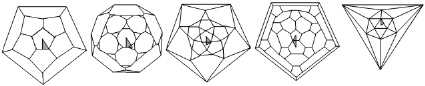
а б в д е
Рис. 1. Проекции оболочек и фундаментальные области группы симметрии Ih для PD{555} (а); tPD{3.10.10} (б); ID{3535} (в); tI {566} (г) и I{33333} (д)
Возможны также следующие преобразования с сохранением симметрии икосаэдра Ih:
икосододекаэдр ID{3535} → усеченный икосододекаэдр tID{46.10} → ромбоикосододекаэдр RID{3454},
усеченный икосаэдр tI{566} → {2{3.10.12} + {3.12.12}} → {3536}.
Характеристики всех полученных выше полиэдров с симметрией икосаэдра Ih, в том числе расчетные значения диаметра соответствующих им фуллеренов и возможные составы оболочек углеродсодержащих наноструктур в соответствии с [30], представлены в табл. 1. Отметим, что в [30] формально допускается также и существование гетероатомных кластеров со структурными формулами AIII60 BII90 в форме икосаэдра, AIII20 BII30 в форме пентагондодекаэдра и AIII30 BII45 в форме икосододекаэдра.
Таблица 1
Характеристика полиэдров с симметрией икосаэдра Ih
|
Полиэдр |
Количество |
Состав фуллерена |
Диаметр фуллерена, нм |
Общая формула |
||
|
вершин |
ребер |
граней |
состава оболочек наноструктур |
|||
|
PD {555} |
20 |
30 |
12 |
C20 |
0,48 |
C20 + 60z |
|
tPD {3.10.10} |
60 |
90 |
32 |
C60 |
0,74 |
C60z |
|
ID {3535} |
30 |
60 |
32 |
C30 |
0,57 |
C30 + 60z |
|
tI {566} |
60 |
90 |
32 |
C60 |
0,74 |
C60z |
|
I {33333} |
12 |
30 |
20 |
C12 |
0,42 |
C12 + 60z |
|
tID {46.10} |
120 |
180 |
62 |
C120 |
1,05 |
C60z |
|
RID {3454} |
60 |
120 |
62 |
C60 |
0,74 |
C60z |
|
2{3.10.12} + {3.12.12} |
180 |
270 |
92 |
C180 |
1,22 |
C60z |
|
{3536} |
90 |
180 |
92 |
C90 |
0,95 |
C30 + 60z |
Аналогичные данные для полиэдров с икосаэдрической симметрией могут быть получены при анализе фундаментальной области точечной группы Ih. Симметрический комплекс группы содержит центр симметрии, 15 поворотных осей симметрии 2-го порядка, 10 инверсионных осей симметрии 3-го порядка, 6 инверсионных осей симметрии 5-го порядка и 15 плоскостей симметрии m. В данном случае фундаментальная область группы – замкнутая неправильная трехгранная пирамида, ребрами которой являются ближайшие друг к другу оси симметрии 2-го, 3-го и 5-го порядка (рис. 2). Положение вершин вероятных многогранников и их локальная симметрия в фундаментальной области точечной группы представлены на рис. 3.
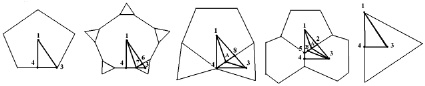
а б в г д
Рис. 2. Соотношения структурных элементов модификаций фуллеренов с симметрией Ih:С20 – PD{555} – (а); С60 – tPD{3.10.10} – (б); С30 – ID{3535} – (в); С60 – tI{566} – (г); С12 – I{33333} – (д)
В [31, 32] методом анализа фундаментальных областей точечной группы симметрии перечислены группы симметрии всех возможных симметрийно неэквивалентных разновидностей молекул фуллеренов, которые могут возникнуть в результате ее непрерывных деформаций. В частности, для молекулы фуллерена С60 выделено 23 различных типа структурных элементов, которым соответствуют 23 типа симметрийно неэквивалентных разновидностей молекулы (рис. 2, г). Число возможных структурных превращений между модификациями определяется как число связей в графе смежности группы Ih и равно 79 [31]. На экстраординарных направлениях A и B симметрия молекулы повышается до m 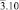 и m
и m 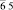 соответственно (табл. 2) [31].
соответственно (табл. 2) [31].
Аналогичный анализ с использованием данных о структурных элементах (рис. 2, а) для получения вероятных деформационных модификаций может быть проведен и для других молекул фуллеренов [32], например, для молекулы С20 в форме пентагонального додекаэдра (табл. 3).
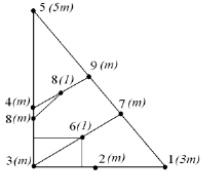
Рис. 3. Положение вершин вероятных многогранников и их симметрия в фундаментальной области точечной группы Ih:1 – PD{555}; 2 – tPD{3.10.10}; 3 – ID{3535}; 4 – tI{566}; 5 – I{33333}; 6 – tID{46.10}; 7 – RID{3454}; 8 – многогранник (2{3.10.12} + {3.12.12}); 9 – многогранник {3536}
Таблица 2
Структурные состояния молекулы фуллерена С60 [31].
|
Структурный элемент * |
Размерность |
Симметрия орбиты |
Собственная симметрия |
|
1 |
1 |
m |
5m |
|
2, 4, 5 |
m |
m |
|
|
3 |
m |
3m |
|
|
A |
m` |
1 |
|
|
B |
m |
1 |
|
|
1–2, 1–5, 2–3, 3–4, 4–5 |
2 |
m |
m |
|
1–A, 2–A, 3–5, 3–B, A–B, B–5 |
m |
1 |
|
|
1–2–A, 1–A–5, 2–3–B, 3–4–5, 3–B–5 |
3 |
m |
1 |
Таблица 3
Структурные состояния молекулы малого фуллерена С20 [32].
|
Структурный элемент * |
Размерность |
Симметрия орбиты |
Собственная симметрия |
|
1 |
1 |
|
5m |
|
4 |
|
2m |
|
|
3 |
|
3m |
|
|
1–3, 1–4, 3–4 |
2 |
|
m |
|
1–3–4 |
3 |
|
1 |
Таким образом, установлено, что при модифицировании КП наноалмазом фазовая и структурная разупорядоченность углеродсодержащих наночастиц на их поверхности после трибовоздействия может быть обусловлена, в частности, наличием фуллереноподобных наночастиц разного состава с диаметром менее 1,25 нм и симметрией точечной группы Ih или ее вероятных деформационных модификаций. В этом случае все эти наночастицы в соответствии с синергической моделью «концентрационной волны» могут рассматриваться как «фазы» твердой компоненты, проявляющие свойства твердых смазочных материалов и эффективно влияющие на трибологические свойства КП [8]. Это подтверждается результатами трибологических испытаний соответствующих твердосмазочных антифрикционных покрытий, полученных с использованием наночастиц алмаза [33].
Работа выполнена при финансовой поддержке Министерства образования и науки РФ, соглашение № 14.U01.21.1078.
Библиографическая ссылка
Дерлугян П.Д., Дерлугян П.Д., Иванов В.В., Иванов В.В., Иванова И.В., Логинов В.Т., Логинов В.Т., Шишка В.Г. ВЕРОЯТНЫЕ ИЗОСИММЕТРИЙНЫЕ И ДЕФОРМАЦИОННЫЕ МОДИФИКАЦИИ ФУЛЛЕРЕНОВ С ОБОЛОЧКАМИ ПЕНТАГОНАЛЬНОЙ ВЕТВИ КЛАССИФИКАЦИИ В АНТИФРИКЦИОННЫХ КОМПОЗИЦИОННЫХ ПОКРЫТИЯХ // Современные наукоемкие технологии. 2013. № 4. С. 26-29;URL: https://top-technologies.ru/ru/article/view?id=31598 (дата обращения: 05.03.2026).




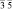
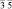
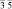

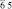
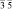
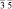
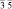
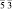 m
m
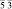 m
m
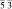 m
m
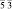 m
m
 m
m