Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Ключевые слова
• Литература

Беззубцева М.М. 1 Волков В.С. 1

---

1 Санкт-Петербургский государственный аграрный университет

Статья в формате PDF

629 KB

1. Беззубцева М.М. Теоретические осно­вы электро­магнитно­го измельчения. – СПб.: Изд-во СПбГАУ, 2005. – 160 с.

2. Беззубцева М.М., Волков В.С. Теоретические основы электромагнитной механоактивации. – СПб.: СПбГАУ, 2011. – 250 с.

3. Кудрявцев Л.С. Максвелл. – М.: Просвещение, 1976. – 145 с.

4. Беззубцева М.М., Мазин Д.А., Зубков В.В. Исследование коэффици­ента объемного заполнения ферромагнитной составляющей в аппара­тах с магнитоожиженным слоем // Известия Санкт-Петербургского аг­рарного университета. – СПб.: Изд-во СПбГАУ, 2011. – С. 371–377.

5. Беззубцева М.М., Ковалев М.Э. Активизация сухих строительных смесей в электромагнитном механоактиваторе с применением эксергетического критерия для оценки эффективности измельчения // Материалы Международной научно-практической конференции / под. ред. А.В. Павлова. – Саратов: Изд-во «КУБиК», 2010.

6. Беззубцева М.М., Волков В.С. Повышение энергоэффективности безотходной технологии производства корма // Материалы Международной научно-практической конференции / под. ред. А.В. Павлова. – Саратов: Изд-во «КУБиК», 2010.

7. Беззубцева М.М. Энергоэффективный способ электромагнитной активации // Международный журнал экспериментального образования. – 2012. – № 5. – С. 92–93.

Преодоление энергии взаимодействия размольных элементов (феррошаров) в рабочем объеме ЭММА [1,2] по аналогии с гипотезой Максвелла о вязкости газа [3] интерпретирована как преодоление некоторой вязкости. Для коэффициента вязкости при представлении его молекул в виде абсолютно упругих шаров Максвелл получил формулу [3]:

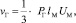(1)

где РГ – плотность газа; lM – средняя длина пробега молекул; UM – средняя скорость молекул.

По аналогии с формулой (1) для зоны взаимодействия размольных тел в рабочем объеме ЭММА [2, 4] рассмотрим формулу:

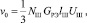(2)

где NШ – число размольных элементов; GРЭ, lШ,, UШ – соответственно масса, средняя длина пробега и средняя скорость одного размольного элемента.

Удельный объем, т.е. объем рабочей камеры, приходящийся на один размольный элемент, можно представить в виде:

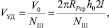(3)

где V0, RРср, 2l – соответственно объем, средний радиус и высота рабочей камеры ЭММА.

Когда притяжение размольных элементов существенно, свободный пробег шара может быть только к ближайшему. Поэтому lШ определяется по формуле:

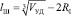(4)

или

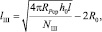(5)

где 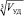– ребро куба, объем которого равен VУД; R0 – радиус размольного элемента.

Таким образом, выражение для эквивалентной вязкости (2) имеет вид:

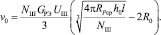(6)

Приняв рабочую гипотезу о независимости скорости шаров UШ от их количества NШ в рабочем объеме ЭММА, исследуем v0 как функцию NШ на экстремум:

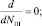
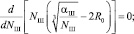
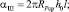
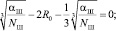
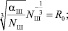
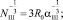
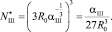(7)

При равенстве 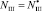значение v0достигает максимума, т.е. процесс помола идет с максимальной интенсивностью:

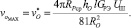(8)

При этом для оптимального объемного коэффициента заполнения рабочей камеры размольными элементами в зоне их переориентации в структурных группах получим:

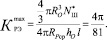(9)

В зонах оснований структурных построений из ферромагнитных размольных элементов [1, 2, 4] объемные коэффициенты заполнения равны отношению объема феррошара к объему описанного около него куба:

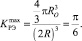(10)

Оптимальный коэффициент объемного заполнения 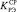для трех зон рабочего объема ЭММА определяется выражением:

(11)

Результаты теоретических исследований подтверждены экспериментальными данными, полученными в результате анализа процесса измельчения продуктов различного целевого назначения [2, 5, 6] в ЭММА различных конструктивных модификаций [7].

Библиографическая ссылка