В геологоразведочной практике на разных стадиях работ широко используются типоморфные признаки главных и примесных минералов руд для оценки уровня эрозионного среза месторождений, положения в рудном теле (фланг, центральное сечение, лежачий, висячий бок рудного тела или месторождения), степени промышленной рудоносности и других геометрических, технологических и экономических параметров по единичным наблюдениям. Известно, что практически все природные минералы содержат в кристаллической структуре точечные дефекты различной природы [1, 4, 6, 7–9]. Концентрация этих дефектов может достигать 10 % и более. Относительно высокая концентрация точечных дефектов в структуре, несомненно, отражается в типоморфизме минералов. Типоморфные свойства минералов, их парагенетические ассоциации определяются РТХ – параметрами их образования, однако, природные вариации количественных значений этих параметров, зависят от многих факторов, изучены не в полной мере. Моделирование минералообразующих процессов на экспериментальном материале предполагает многочисленные ограничения в практическом использовании. Поэтому косвенная связь концентраций золота в горных породах и рудах и типоморфных свойств сопутствующих минералов, выражающаяся сложными математическими уравнениями, является объектом пристального внимания при количественном прогнозировании. Геологическими исследованиями многочисленных золоторудных месторождений установлены ассоциирующие с золотом минералы, на минералогическом признаке проведена типизация месторождений, однако, качественная и количественная корреляция содержания золота в рудах с типоморфными свойствами минералов исследована пока не достаточно. Эти вопросы в настоящее время приобретают особую актуальность в связи с расширением золотодобычи в стране, что требует переоценки известных месторождений, поиском и прогнозированием новых золотоносных объектов. Пирротин различного химического состава и с различной плотностью примесных атомов часто встречается в золотосодержащей руде. Интерес представляет количественное сопоставление примесных атомов различной природы в пирротине различных месторождений, а также изучение закономерностей их распределения в структуре пирротина различного состава, с процентным содержанием золота как в кристаллической структуре пирротина, так и в золотоносной породе. Примесные элементы искажают кристаллическую структуру основной структурной матрицы. Их влияние на свойства минералов исследовано фрагментарно, хотя роль таких искажений, вызванных зачастую именно примесными атомами, может оказаться, в ряде случаях, доминируюшей..
В настоящем сообщении рассматриваются типоморфные кристаллохимические свойства пирротина золоторудных месторождений «Панимба» и «Благодатное» в Енисейском кряже (Красноярский край). Отличительной особенностью пирротинов месторождения «Панимба» является содержание золота в кристаллической структур, в то время, как пирротины месторождения «Благодатное», не имели в структуре атомов золота, но, при этом, часто его оказывается достаточно много в руде. Причины содержания золота в структуре пирротина одних месторождений и отсутствие его в структуре пирротина других месторождений не ясны до настоящего времени и, несомненно, вызывают интерес.
Цель исследования:
а) расcчитать на основе предложенного Онуфриенком [5, 7] алгоритма плотность примесных атомов в структуре пирротина;
б) сопоставить расчетную плотность для каждого сорта примесного атома в структуре пирротинов месторождения «Панимба» и «Благодатное» и выявить основные отличия в законах из распределения в структуре;
в) проанализировать содержание золота в породе и в структуре минерала сопоставив его с плотностью примесных атомов различной природы в структуре пирротинов месторождения «Панимба» и «Благодатное»;
г) установить роль различного рода дефектов в кристаллохимических превращениях в пирротинах.
Материал и методы исследования
Исследовался пирротин из месторождения «Панимба» и «Благодатное» в Енисейском кряже (Красноярский край, Россия). Химический состав изучаемых пирротинов определялся рентгеноспектральным методом (XRS) на установке «Camebax-Miсro» в лаборатории микрозондового анализа СО РАН. Кристаллическая структура и фазовый состав образцов контролировались методами РФА на дифрактометре XRD-7000S фирмы Shimadzu с использованием рентгеновского излучения Сu(Кα). Расчет плотности точечных дефектов в структуре пирротина осуществлялся по формулам, предложенным в работе [5, 7].
Результаты исследования и их обсуждение
Для анализа различного рода точечных дефектов в пирротине необходимо рассмотреть его кристаллическую структуру. Пирротин обладает кристаллической структурой типа NiAs (В-8). Базисная элементарная ячейка такой структуры содержит два катиона и два аниона (структура с базисной элементарной ячейкой 1С). Отличие от стехеометрического состава объясняется тем, что часть катионных позиций вакантна [1, 3, 5, 7]. Ранее была предпринята попытка выявить зависимость геохимических свойств и особенностей распределения золота в руде, проявляющиеся в химическом составе и кристаллической структуре пирротинов месторождения «Благодатное», кристаллическая структура которых не содержала атомов золото в виде точечных дефектов [4]. Также была предпринята попытка выявить зависимость геохимических свойств и особенностей распределения золота в кристаллической структуре пирротинов месторождения «Панимба», кристаллическая структура которых содержала атомов золото в виде точечных дефектов [6]. В представленной работе интересно сопоставить результаты этих отдельных исследований и выявить основные отличия в распределении примесных атомов в структуре пирротина.
Для нестехиометрических минералах со структурой типа NiAs, содержащих катионы с атомным весом Мк и анионы с атомным весом Ма, максимальное содержание примесных атомов, при их полном заполнении всех вакантных позиций в структуре, можно рассчитать по формуле:
φ = {(x – 1)y100}/{y(x – 1) + (Max + Mk)}, (1)
где у – атомный вес катионов внедрения.
Для определенности, отношение х = А/К можно выбрать такое же , как и у пирротинов, т.е. 1 < x < 1,2. Заметим, что для пирротинов А –это сера, а К – железо. Очевидно, что в общем случае А и К могут быть другие элементы и другое их соотношение в минерале.
На основе XRS анализа химического состава природных минералов следует, что атомы внедрения занимают обычно не все вакантные позиции, а только определенную их часть. Тогда для расчета концентрации атомов внедрения необходимо знать массовый процент внедренных элементов, определяемый для минералов обычно методами рентгеноспектрального анализа.
В этом случае концентрацию примесных атомов можно рассчитать по формуле:
β = αтабл[(1 – 1/x)/φ(x)]. (2)
Из представленной схемы расчета точечных дефектов следует, что любое нестехиометрическое соединение может быть записано в виде химической формулы:
KγВβA, (3)
где А и К соответственно анионы и катионы основной кристаллической матрицы, а В – катионы внедрения в вакантные позиции этой матрицы, γ = 1/x. Число вакантных позиций, нормированных на один узел кристаллической структуры, легко определить из уравнения:
ν = 1 – γ – β. (4),
Поскольку γ = 1/x, где х есть соотношение А/К, то но основе формулы (4) можно формулы (1), (2) представить как функции от концентрации вакансий ν, т.о. возможно в данном случае представление функциональных зависимостей от концентрации катионных вакансий в структуре. Атомы основной матрицы (железа и сера) выбраны для примера. В общем случае, атомы кристаллической матрицы могут быть хром и никель, никель и селен, сера и хром и т.д.
Атомы включения (Co, Ni ,Cu и Au) занимают, как правило, вакантные катионные позиции. Очевидно, что в пирротине катионные позиции предпочтительно занимают те атомы, ионы которых имеют размеры близкие к радиусам ионов двухвалентного железа (Fe2+ – 0,82 Ǻ). Примером могут служить никель и кобальт, ионные радиусы которых имеют значение: Co2+ – 0,72 Ǻ; Ni2+ – 0,69 Ǻ. Для катионных вакансий ионный радиус равен, очевидно, нулю, а для золота (Au2+) – 1,26 Ǻ. Это два крайних случая максимального локального искажения кристаллической структуры при их наличии в ней, поэтому представляет интерес рассмотреть закономерности при замещении вакантных позиций ионами кобальта и никеля в структурах, содержащих золота и при его отсутствии. На рис. 1, 2 графически представлены результаты расчетов примесных атомов кобальта и никеля соответственно в структуре пирротина месторождений «Панимба» и «Благодатное».
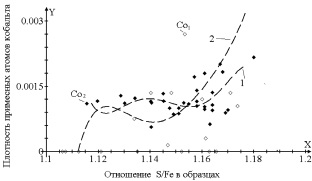
Рис. 1. Зависимость плотности кобальта от соотношения серы и железа в структурах пирротина двух различных месторождений. Кривая 1 – пирротины месторождения «Благодатное», кривая 2 – пирротины месторождения «Панимба»
Аналитически эти зависимости в указанных интервалах можно представить в виде формул:
2510,7x9 – 8109,1x8 + 6096,6x7 – 723,3x6 + 10962,2x5 – – 17197,4x4 + 8458,7x3 – 13210,1x2 + 19035,9x – 7826,4
для кривой 1 при стандартном отклонение δn = 0,01;
–16439,1x7 + 66873,4x6 – 80206,7x5 + 9342,2x4 – 9930,7x3 ++ 119910,6x2 – 132681,7x + 43136,6
для кривой 2 при стандартном отклонение δn = 0,003.
Таким образом, даже детальное теоретическое описание кривых 1 и 2 принципиальных отличий в поведении плотности примеси кобальта не удалось обнаружить. Заметим, что ионный радиус кобальта имеет наилучшее совпадение с ионами материнской матрицы.
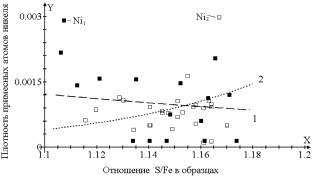
Рис. 2. Зависимость плотности никеля от соотношения серы и железа в структурах пирротина двух различных месторождений. Кривая 1 – пирротины месторождения «Благодатное», кривая 2 – пирротины месторождения «Панимба»
Аналитическое сравнение функциональных зависимостей в указанных интервалах в виде полиномиальных функций: 0,1671262·0,0113992x для кривой 1 при стандартном отклонение δn = 0,0016181; R2 = 0,0062 показывает спад плотности никеля при увеличении отношения S/Fe в образцах, а для кривой 2 –(8,1011016·10–12)·(9,9003519·106)x при стандартном отклонение δn = 0,00114; R2 = 0,08 показывает рост плотности никеля при увеличении отношения S/Fe в образцах.
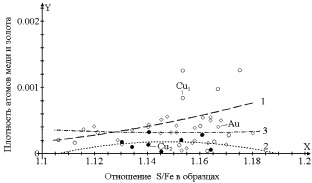
Рис. 3. Зависимость плотности меди от соотношения серы и железа в структурах пирротина двух различных месторождений. Кривая 1 – пирротины месторождения «Благодатное», кривая 2 – пирротины месторождения «Панимба». кривая 3 – плотность ионов золота в структуре пирротина месторождения «Панимба»
Аналитически эти зависимости в указанных интервалах можно представить в виде формул:
0,039x2 – 0,082x + 0,043 для кривой 1 – показывает рост плотности меди при увеличении отношения S/Fe в образцах при стандартном отклонение δn = 0,000416; R2 = 0,1467:
–0,1026x2 + 0,235x – 0,135 – кривая 2, она показывает спад плотности меди при увеличении отношения S/Fe в образцах при стандартном отклонение δn = 0,000103; R2 = 0,0129:
кривая 3: 0,0198x2 – 0,0456x + 0,0265 показывает зависимость плотности золота при увеличении отношения S/Fe в образцах при стандартном отклонение δn = 0,000158; R2 = 0,00146.
На рис. 4 (кривая 1) представлена экспериментально полученная зависимость I/I0 для сульфидов железа с различной концентрацией вакансий в структуре [2]. Эта кривая может описываться с хорошей точностью аналитической формулой, выведенной в работе [2] на основе квантовых представлений взаимодействия вакансий:
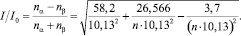
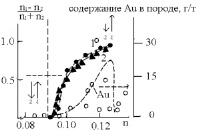
Рис. 4. Зависимость концентрации катионных вакансий от степени их упорядочения и содержания золота в породе
Здесь сопоставлены плотность вакансий в пирротине и их упорядочение в структуре с содержанием золота в породе – в графическом представлении доказана корреляция между этими процессами. Более подробно этот факт изложен в работе [7] и обсуждался на конференции прикладной минералогии ICAM (Норвегия).
Если при формировании пирротина вакантную катионную позицию занимает атом, размеры которого значительно превышают размеры иона железа, то, очевидно, кристаллическая решетка в этом месте будет сильно деформироваться. Система, стремясь минимизировать потенциал Гиббса и занять состояние с минимумом свободной энергии, будет стремиться вытолкнуть из структуры такие атомы (например, золота). В кристаллической структуре пирротина при этом возрастает концентрация катионных вакансий.
Рост концентрации этих атомов в кристаллической структуре должен сопровождаться возрастанием числа вакантных позиций. Эта зависимость и наблюдается на практике [8–9]. Таким образом, рост числа вакансий сопровождается ростом числа суммарных точечных дефектов. Ясно, что чем больше атомов тяжелых металлов, в нашем примере, золота, вытолкнуто кристаллической структурой, тем больше катионных вакансий будет содержать пирротин и тем меньше концентрация золота в пирротине. Из данной модели следует предположить, что если в золотоносной породе пирротин содержит относительно большую концентрацию вакантных катионных позиций, то и атомов золота в кристаллической структуре пирротина должно быть меньше.
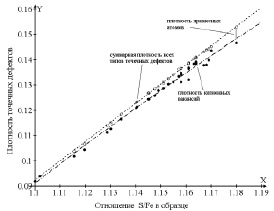
Рис. 5. Зависимость концентрации точечных дефектов и концентрации катионных вакансий от соотношения серы и железа в пирротине
На рис. 5 представлены зависимости концентрации всех точечных дефектов и концентрации катионных вакансий от соотношения S/Fe в пирротине. Концентрацию внедренных атомов для пирротина определенного состава можно определит в виде разности значений функций, представленных кривыми 1 и 2 на рис. 5 при фиксированном значении x. Следует отметить, что концентрация суммарных дефектов носит практически линейный характер, а зависимость концентрации катионных вакансий не линейна. Из характера кривых рис. 5 можно заключить, что концентрация катионных вакансий имеет насыщение, т.е. существует некоторое критическое значение концентрации катионных вакансий nk, после которого (т.е. если n > nk) реализуется фазовый переход (например, в пирит). Отметим, что возможны метастабильные состояния кристаллической структуры пирротина с перенасыщенной концентрацией вакансий, когда n = nk + Δn. Для того, чтобы исключить влияние атомов внедрения в кристаллическую структуру, были синтезированы пирротины в интервале соотношений S/Fe образцах. Гомогенные образцы получались до соотношения S/Fe, равное 1,18. Следовательно, в данном случае n = 0,153. После тридцатилетней выдержки образцов в лабораторных условиях повторный XRS и XRD анализ показал, что максимальное соотношение серы и железа в гомогенных образцах не превышает 1,14. Если предположить, что выдержанные образцы перешли в стабильное состояние, то значение nk = 0,125, а Δn = 0,028. Расчет катионных вакансий произведен по методике. При сравнении критической концентрации катионных вакансий в кристаллической структуре пирротинов, содержащих атомы внедрения (nk = 0,1467), можно заключить, что атомы внедрения стабилизируют критическую концентрацию вакансий нестабильных пирротинов.
Все же заметим, что критическая концентрация вакансий нестабильных пирротинов превышает критическое значение концентрации катионных вакансий в структуре природных пирротинов, содержащих атомы внедрения. Отметим, что гомогенными природные пирротины остаются до соотношения S/Fe, равного 1,18. Линейный характер точечных дефектов можно объяснить тем, что, например, атомы никеля или кобальта замещают атомы материнской матрицы (т.е. железа), хотя, возможно, и в этом случае существует какая-та критическая концентрация внедренных атомов. Можно предположить, что критическая концентрация атомов внедрения существенно превышает nk, этим и объясняется различный характер поведения данных функций (рис. 5).
Анализ синтетических пирротинов позволяет заключить, что существует определенная начальная концентрация (n0) катионных вакансий. Образцы в интервале составов FeS – FeS1,03 не были гомогенными, а состояли из двух фаз FeS и FeS1,03. Следовательно, начальная концентрация катионных вакансий равна n0 = 0,029. Меньше этого значения концентрация катионных вакансий невозможна как у синтетических, так и у природных пирротинов. Тем не менее, остается не ясным влияние на это значение атомов внедрения различной природы. Синтетические пирротины в интервале составов FeS1,03–FeS1,18 были практически гомогенными, т.е. концентрация вакансий в структуре этих образцов изменялась достаточно плавно. Возможно, что и для концентрации атомов внедрения существует аналогичный параметр n0. Таким образом, концентрация внедренных атомов может иметь некоторое предельное значение, меньше которого в структуре пирротинов не существуют внедренные атомы. Можно предположить, что эта величина зависит от рода атомов внедрения, от концентрации катионных вакансий и от соотношения серы и железа в образцах. Например, как следует из рис. 1‒3, атомов внедрения нет при соотношении S/Fe менее 1,115. Концентрация катионных вакансий для этого образца равна 0,1018, это значение и будет определять в данном случае параметр n0 для пирротинов. Такая концентрация вакансий соответствует синтетическому пирротину состава FeS1,113, а природный пирротин c такой же концентрацией катионных вакансий имеет состав FeS1,115. Ясно, что природный пирротин отличается от синтетического, в данном случае, наличием в кристаллической структуре атомов внедрения. Очевидно, что все эти вопросы нуждаются в дальнейших детальных исследованиях. Предложенная методика расчета точечных дефектов является необходимым фактором для подобных работ.
Выводы
На основании теоретических вычислений и экспериментальных данных установлено:
а) если ионные радиусы примесного атома (Co) и атома материнской кристаллической матрицы (Fe) близки по значению, то с увеличением соотношения S/Fe в образцах плотность примесных атомов в структуре пирротина возрастает;
б) концентрация внедренных атомов, концентрация катионных вакансий, а также суммарная концентрация всех точечных дефектов возрастают с увеличением содержания серы в пирротине, причем, если концентрация суммарных дефектов носит практически линейный характер, то зависимость концентрации катионных вакансий нелинейна;
в) с увеличением соотношения S/Fe плотность атомов золота в структуре пирротина носит практически линейный характер, хотя и демонстрирует небольшой сад;
г) если ионные радиусы примесного атома (Cu) и атома материнской кристаллической матрицы (Fe) достаточно отличны по значению, то с увеличением соотношения S/Fe в образцах, плотность примесных атомов в структуре пирротина выражается достаточно сложной зависимостью;
д) предложена химическая формула для нестехиометрических минералов со структурой типа NiAs, содержащих в кристаллической структуре атомы, отличные от атомов образующей матрицы.
е) примесные атомы стабилизируют критическую концентрацию катионных вакансий пирротинов;
ж) определены аналитические функциональные зависимости для пирротина месторождения «Панимба» и «Благодатное» – спад плотности никеля при увеличении отношения S/Fe в образцах, в структуре которых нет атомов золота, а для пирротинов, содержащих в структуре ионы золота, наблюдается рост плотности никеля при увеличении отношения S/Fe в образцах;
з) сопоставлены плотность вакансий в пирротине и их упорядочение в структуре с содержанием золота в породе – в графическом представлении доказана корреляция между этими процессами.
Библиографическая ссылка
Онуфриенок В.В. СРАВНИТЕЛЬНЫЙ АНАЛИЗ РАСПРЕДЕЛЕНИЯ ПРИМЕСНЫХ АТОМОВВ СТРУКТУРЕ ПИРРОТИНА ЗОЛОТОСОДЕРЖАЩИХ РУД // Современные наукоемкие технологии. 2013. № 3. С. 51-57;URL: https://top-technologies.ru/ru/article/view?id=31505 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/snt.31505



