В [1] сформулированы концептуальные основы и алгоритм построения человекомерной модели технической энергосистемы. Для объекта моделирования построены схемы наполнения соответствующих энергетических состояний. В [2] намечены связи между технической и социальной частями модели. Показано, что субъект создает вокруг себя энергосистему для выработки, передачи, распределения и потребления разных форм энергии. Энергия используется для выпуска разного рода продукции. Процессы выпуска продукции управляются энергетическим субъектом человеком, через его понимание реакции окружающей среды. Все зависит от уровня формирования компетенций полученных в процессе получения знаний, о которых указано в социальном блоке [1, 5]. Принятый выше концептуальный подход, позволяет строить модель системы, последовательно настраивая один блок системы за другим путем подбора обобщенных интегральных [3] энергетических показателей позволяющих регулировать структуру технологического процесса, меняя параметры ЭС, среди которых качество и количество выпускаемой продукции. Рассмотрение подобных моделей не только облегчают условия создания новых блоков в энергосистеме (ЭС) при изменении условий принуждения [3], но и сопутствуют внедрению моделей в системы получения и передачи знания [4, 5].
Рассмотрим примеры построения модели технологического процесса, в структурируемых пространствах состояния Субъект–Объект привязанных к деятельности предприятия выпускающего продукцию. Поскольку объект является технической энергетической системой, то субъекта в первую очередь интересует функции потенциала энергосбережения каждого конструктивного блока участвующего в выпуске продукции [2, 3, 6, 7, 8]. В [7] решение задачи рассматривается в терминах пространства состояния записанного в макро и мета иерархических уровнях. Рассмотрим сначала метауровневый подход. Выходная траектория развития энергосистемы во времени в этом случае является зависимой от комплекса функций, описывающих энергетическое состояние каждого блока и всей ЭС предприятия. Это функции интегральных потенциалов электроемкости, теплоемкости, энергоемкости выпускаемой продукции, характеризующие уровень энергетического состояния предприятия [6].
Идентификация энергоэффективных режимов работы ЭС требует от субъекта как минимум сопоставления двух моделей априорного и апостериорного содержания [3, 4].
Запишем функциональное обобщенное уравнение, показывающее траекторию развития или деградации ЭС(1)
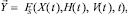(1)
где FS – оператор, указывающий на функцию энергетического состояния организованной диссипативной технической ЭС;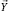 
– вектор параметров выходной траектории системы, описываемый с помощью оператора FS множества входных X, выходных Y, внутренних H, внешних V параметров, [2, 3].
Начальные и граничные условия, заложенные в формулы (2), (3), позволяют субъекту сравнивать между собой образы ЭС последовательно применяя процедуры синтеза и анализа для моделей объектов существующих и вновь создаваемых, записанных до, и после внедрения энергосберегающих мероприятий, как в координатном, так и во временном энергетических состояниях.
Например, для нормативных данных, используемых в проектировании имеем зависимость (2)
Ys нор = Fsн (z0н; zн(t)), (2)
для данных, полученных после энергетического экспериментального обследования (3)
Ysдэо = Fsдэо (z0; zдэо(t)). (3)
Разность выходных траекторий изменения энергетических состояний даст (4)
Ysнор – Ysдэо = ∆Yпэ. (4)
В (2) и (3) (z0н; zн (t)), (z0; zдэо (t)) – множества начальных условий z0 и функции z(t) выраженные через параметры уравнения (1). Множество (4) указывает на энергетический потенциал энергосбережения для фактически существующей энергообследуемой ЭС, на сверхнормативный перерасход энергии, т.е. на энергию диссипативного плана. Она превращается в теплоту и уходит в окружающую среду не совершая полезного для субъекта эффекта. ЭС, которая имеет сверхнормативный избыток диссипационной энергии требует схемотехнической переструктуризации модели. Субъект выбирает из множества предлагаемых энергосберегающих мероприятий, те мероприятия, которые устраняют сверхнормативные потери.
Например, функциональный вектор ЭС выражен через три основные структуры, то запись в виде энергетического пространства состояния имеет вид (5)
Sо = [F1; F2; F3], (5)
где F1; F2; F3 – структурные функциональные координаты вектора, под которыми понимаются операторы соответствующих пространственно временных функциональных уравнений. Каждый структурный блок имеет в соответствии с моделью свое эквивалентное схемотехническое описание.
Пусть модернизированному источнику теплоты F1 соответствует структурная модель
Sи = [F11; F12], (6)
где F12 это оператор модели энергосберегающего мероприятия. Он имеет свое схемотехническое решение, вписанное в систему (6). Задача, решаемая субъектом состоит в том, чтобы в структурный элемент имеющий свое энергетическое пространство состояния вставить пространство состояния другого структурного элемента энергетическое состояние, которого эквивалентно эффекту от внедрения энергосберегающего мероприятия.
Искомая модель строится в результате последовательного применения процедур синтеза и анализа для двух подсистем. Получается новая ЭС, имеющая свое пространство состояния и новые параметрические свойства. Итерационная процедура анализа для элементов вектора Sи должна подтвердить уравнение (6) и подразумевает проверку условия ∆Y → 0. Если величина ∆Y → 0 достаточно мала и отвечает заданным граничным и начальным условиям, то можно говорить о правильном выборе энергосберегающего мероприятия и о том, что величина приближения диссипационной составляющей реальной системы ∆Y → min. Это условие сохранятся за все время работы ЭС. Отклонение энергетического состояния от этого условия указывает на необходимость проведения повторного энергетического обследования.
Рассмотрим пример вычисления потенциала энергосбережения для блока F1.
Структурное координатное энергетическое состояние соответствующее схемотехническому решению для стандартного источника теплоты в виде котельной подразумевает функциональную модель вида (7) с координатными функциями, рис. 1,
Y = Fсист [f1; f2; f3; f4; f5; f6; f7; f8; f9]. (7)
Элементы координатной матрицы представляют собой энергетическое состояние основных блоков ЭС: f1 – группа котлоагрегатов; f2 – подогреватель сетевой воды; f3 – деаэратор; f4 – сепаратор непрерывной продувки котлов; f5 – химводоочистка; f6 – подогреватель подпиточной воды; f7 – подогреватель химически очищенной воды; f8 – газо-мазутные горелки; f9 – мазутное хозяйство. Yкот – группа параметров описывающих выходную траекторию состояния схемы. Fсист1 – оператор указывающий на функциональное состояние ЭС. Каждый элемент матрицы является узлом координатной сетки ЭС и служит для выработки продукции в формах тепловой и механической энергии.
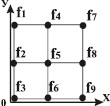
Рис. 1. Координатные функции и организация энергетического пространства состояния
Условия нужной глубины анализа требуют перехода ну другой потоковый иерархический уровень построения модели. Для этого составляются функциональные уравнения для i-го количества основных структур. Выявляются типичные j-е потоковые связи между блоками (8)
(fi3, fi2) = F1п (fi1, fi4, fi5, fi6), (8)
которые обеспечивают функционирование каждого блока. Здесь главные интересующие субъекта из fij потоки вещества и энергии: fi2 поток теплоты, fi3 –поток электрической энергии. (fi1, fi4, fi5, fi6) – группа вспомогательных потоков, обеспечивающих тепловые и электрические составляющие. Пусть fi7 – поток основной продукции котельной, а энергетический потенциал каждого блока определяется через сумму удельных энергетических потенциалов, таких как теплоемкость, электроемкость, энергоемкость единицы выпускаемой продукции. Тогда потенциалы для каждого i-го элемента блока равны (9), (10), (11):
● теплоемкости
тпi = fi2/fi5, (9)
● электроемкости
эпi = fi3/fi5, (10)
● энергоемкости продукции
эпотi = тпi + эпi = (fi2 + fi3)/fi5. (11)
● знание потенциалов энергоемкости для каждого блока позволяет найти сумму из n потенциалов. Она определяет энергетический потенциал всей системы 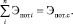(13)
(13)
Разность экспериментально полученных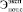 
и проектных энергетических потенциалов 
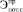системы 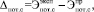(14)
(14)
дает потенциал энергосбережения ЭС. Аналогичным образом вычисляются потенциалы энергосбережения для каждой из подсистем котельной. Если Dпот.э.с. > 0, то нужно искать способы уменьшения энергетического потенциала, если Dпот.э.с < 0, то требуется обосновать причины отрицательного его значения.
Матрицы потенциалов в координатном пространстве объекта для экспериментальной модели имеют вид Мэ (15) для проектной Мп (16).
(15)
(16
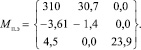(17)
Вычитая из (15) (16) получим численные значения координатной функции потенциала энергосбережения для каждого энергетического узла ЭС котельной (17) (рис. 2). Потенциал энергосбережения в координатном пространстве ЭС самый высокий для функции f1 = 310 т.у.т. в год.
Выводы по работе. Работа является продолжением работ [1, 2, 3] в рамках темы – «Поиск обобщенного интегрального энергетического показателя в условиях интеграции и трансформации наук существующего знания».
Проведен анализ процессов энергосбережения на примере реального источника тепломеханической энергии с помощью модели построенной с использованием понятий энергетического пространства состояния ЭС [2, 3].
На основе положений указанных в энергетической стратегии России до 2020 г. выбран для анализа обобщенный интегральный показатель в виде потенциала энергоемкости выпускаемой продукции [6].
Показан вывод этого показателя через потенциалы теплоемкости, электроемкости выпускаемой продукции энергетического объекта и применение удельного потенциала энергоемкости к определению потенциала энергосбережения. Получены обобщенные аналитические выражения для построенных функций.
С помощью аналитических выражений определены особенности выбора энергосберегающих мероприятий из условия минимума диссипативной составляющей исследуемой энергетической системы.
Введено понятие координатных функций в пространстве энергетического состояния энергетического объекта (рис. 2).
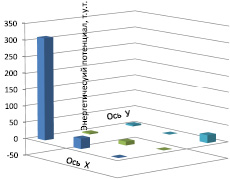
Рис. 2. Координатные функции потенциала энергосбережения
На основе разработанной методики моделирования проведена структуризация реального энергетического объекта в виде источника тепломеханической энергии. Определены параметры состояния идентифицированных структур.
Обоснованы практические рекомендации для моделирования потенциалов энергосбережения и условия выбора энергосберегающих мероприятий.
Сформулированы в терминах неравновесной термодинамики условия повторного проведения энергетического обследования (энергоаудита).
Определены для источника теплоты структуры, для которых в первую очередь надо вести выбор энергосберегающих мероприятий.
Библиографическая ссылка
Игонин В.И. Методика определения координатных функций потенциала энергосбережения для объекта через понятия энергетического пространства состояния // Современные наукоемкие технологии. – 2013. – № 3. – С. 29-32;URL: https://top-technologies.ru/ru/article/view?id=31500 (дата обращения: 19.04.2024).