Объектом исследования являются методы криптографических преобразований данных. Предмет исследования – криптостойкость. Исходные данные представлены в виде цветного изображения в формате gif, 400×296 пикселей. Алгоритмы шифрования – гаммирование, DES, TripleDES, Rijndael; режимы шифрования – ECB, CBC, CFB. Поиск энтропии исходных и зашифрованных данных осуществляется по классической формуле Шеннона [2]. Выявлены два подхода к определению энтропии изображений (RGB):
‒ энтропия изображения находится как сумма энтропии каналов изображения;
‒ энтропия изображения вычисляется в зависимости от вхождений цветов в изображение.
В первом подходе [3] для расчета энтропии изображения Н(Х) необходимо определить энтропию каждого из каналов изображения. Пусть вектор С – канал изображения X, С = {R, G, B}. Тогда энтропия канала изображения определяется по формуле Шеннона:
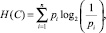
где С – канал изображения Х; pi – вероятность, определяемая как частное от деления количества появлений i-го байта (i = 0...255) в канале изображения С к числу байт канала С изображения Х. Так как энтропия независимых источников равна сумме энтропии источников, то энтропия всего изображения H(X) определяется как сумма энтропии каналов изображения:
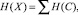
где С – канал изображения Х, С = {R, G, B}.
В соответствии со вторым подходом энтропия изображения вычисляется по формуле Шеннона, однако вероятности определяются иным образом:
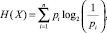
где Х – изображение; pi – вероятность, определяемая как частное от деления количества вхождений пикселя i-го цвета (RGB) к количеству пикселей изображения Х.
Пусть H1(Х) и H1(Y) – энтропии исходного и зашифрованного изображения, рассчитанные первым способом, а H2(Х) и H2(Y) – вторым способом соответственно. Энтропия зашифрованного изображения, «зашумленного» ранее, рассчитанная первым и вторым способом – Нga1(Y) и Нga2(Y). Начальная энтропия H1(X) = 14,81, H2(Х) = 5,57.
При использовании и первого, и второго способа расчета энтропии наблюдается схожая тенденция – шифрование в режиме ECB является наиболее «слабым», что подтверждается визуально. Наиболее «сильным» является шифрование DES, TripleDES, Rijndael в режиме CBC, при «зашумлении» исходных данных – Rijndael в режиме CBC. Энтропия Нga1(Y) и Нga2(Y) практически не меняется относительно Н1(Y) и Н2(Y), а в ряде случаев – значительно меньше. Таким образом, выполняемые преобразования над исходными данными существенно не добавляют вариации цвета изображения. Недостатком подхода является то, что энтропия не учитывает сложность формирования структуры данных и если изображение зашумлено, то оно всё равно формально обладает большим количеством информации [4]. Следовательно, оценивание на основе энтропии не является достаточным условием для принятия решений о стойкости криптопреобразований.
Библиографическая ссылка
Сен Н.Д., Котляров В.П., Григорьев Я.Ю. ПРИМЕНЕНИЕ ОЦЕНОК НА ОСНОВЕ ЭНТРОПИИ ДЛЯ СРАВНЕНИЯ КРИПТОСТОЙКОСТИ АЛГОРИТМОВ ШИФРОВАНИЯ // Современные наукоемкие технологии. 2013. № 2. С. 105-106;URL: https://top-technologies.ru/ru/article/view?id=31343 (дата обращения: 13.03.2026).



