Дистрибутивным асинхронным автоматом называется пятерка (S, s0, E, I, Tran), состоящая из множеств S и E, элемента s0 ∈ S, отношения Tran ⊆ S×E×S и семейства антирефлексивных симметричных отношений I ⊆ (Is)s ∈ S, Is ⊆ E×E. Должны быть выполнены следующие условия:
i Если (s, a, s′) ∈ Tran и (s, a, s″) ∈ Tran, то s′ = s″
ii Для любых
s ∈ S, (a1, a2) ∈ Is, (s, a1, s1) ∈ Tran, (s1, a2, s′) ∈ Tran,
существует такое s2 ∈ S, что (s, a2, s2) ∈ Tran и (s2, a2, s′) ∈ Tran (см. рисунок).
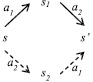
Аксиома (ii) для дистрибутивных асинхронных автоматов
Всякую асинхронную систему (S, s0, E, I, Tran) можно рассматривать как дистрибутивный асинхронный автомат, полагая Is = I для всех s ∈ S.
Определим сеть Петри как пятерку (P, T, pre, post, M0), состоящую из конечных множеств P и T, функций M0:P → N, pre: T → NP, post: T → NP . Здесь NP обозначает множество всех функций P → N. Элементы p ∈ P называются местами, t ∈ T – переходами, M ∈ NP – маркировками, а M0 – начальной маркировкой. Определим отношение порядка на NP, полагая M ≤ M′, если для всех p ∈ P верно M(p) ≤ M′(p). Сумму и разность функций определим как (M ± M′)(p) = M(p) ± M′(p). Для M, M′ ∈ NP и t ∈ T запись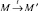 
будет означать, что выполнены условия M ≥ pre(t) и M′ = M – pre(t) + post(t) . В этом случае будем говорить, что маркировка M′ получена из M с помощью срабатывания перехода t.
Пусть (P, T, pre, post, M0) – сеть Петри. Обозначим t = {p ∈ P: pre(t)(p) ≠ 0}. Сеть Петри (P, T, pre, post, M0) определяет дистрибутивный асинхронный автомат (S, s0, E, I, Tran), S = NP, E = T, s0 = M0, Tran = {(M, t, M′) ∈ NP×T×NP существует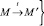 
, для которого Im = {(t1, t2) ∈ T×T:M ≥ pre(t1) и t1 ∩ t2 = ∅}.
Временная сеть Петри это кортеж (N, eft, lft), где N – сеть Петри, eft: T → N, lft: T → N – функции, описывающие соответственно раннее и позднее время доступности переходов, которые удовлетворяют ограничению eft(t) ≤ lft(t) для каждого t ∈ T. Обобщим определение временной сети Петри. Обозначим через R≥0 множество всех неотрицательных вещественных чисел. Временным дистрибутивным асинхронным автоматом (A, eft, lft) называется дистрибутивный асинхронный автомат A = (S, s0, E, I, Tran) вместе с парой функций eft: E → R≥0, lft: E → R≥0 ∪ {∞}, удовлетворяющих для всех a ∈ E неравенству eft(a) ≤ lft(a).
Введем временные состояния. Определим отображение S×E → S⊔{*}, полагая s∙a = s′, если (s, a, s′) ∈ Tran. Если таких s′ ∈ S не существует, то положим s∙a = *. Временным состоянием временного дистрибутивного асинхронного автомата (A, eft, lft) называется пара (s, h) , состоящая из s′ ∈ мS и функции h: E → R≥0 ∪ {#}, таких что s∙a ∈ S ⇒ h(a) ≤ lft(a) и s∙a = * ⇒ h(a) = #. Каждое действие a ∈ E имеет «часы». В начале работы временное состояние равно (s0, h0), где h0(a) = 0, если существует s′ ∈ S и переход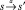 
.
Рассмотрим асинхронную систему, состоящую из двух независимых действий a1 и a2 и четырех состояний
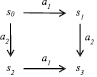
для которых известные ft(ai) и lft(ai), i ∈ {1, 2}. Вычислим минимальное время выполнения операций, приводящих к состоянию s3. Временные состояния (s, h) будем рассматривать как тройки (si, τ1, τ2). Пусть eft(a1) ≤ eft(a2). Тогда возможен следующий путь выполнения:
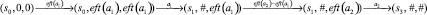
Легко видеть, что полученное время, равное сумме eft(a1) + eft(a2) – eft(a1) будет минимальным. Следовательно, в общем случае минимальное время будет равно max (eft(a1), eft(a2)). Аналогично получим, что максимальное время выполнения действий будет равно max (lft(a1), lft(a2)).
Библиографическая ссылка
Кудряшова Е.С., Хусаинов А.А., Лошманов А.Ю. ВРЕМЕННЫЕ ДИСТРИБУТИВНЫЕ АСИНХРОННЫЕ АВТОМАТЫ // Современные наукоемкие технологии. – 2013. – № 2. – С. 104-105;URL: https://top-technologies.ru/ru/article/view?id=31342 (дата обращения: 21.11.2024).