Согласно теории осадкообразования Финдайзена-Бержерона, введение в облако некоторого дополнительного количества ядер кристаллизации, может привести к ускорению роста капель, увеличению их числа, интенсификации восходящего потока за счёт дополнительного тепловыделения при переходе воды в кристаллическую фазу и т. д. При этом может интенсифицироваться процесс осадкообразования. В других ситуациях, если ввести очень много таких ядер, то, предполагая ограниченность энергетического ресурса данного термодинамического процесса, можно привести облако к «паровому голоду» либо к интенсификации процесса образования осадков за счёт усиления восходящего потока.
В ряде случаев на стадии диссипации облака можно интенсифицировать нисходящий поток. Всё это может приводить к увеличению, на стадии развития, или к уменьшению, на стадии диссипации, периода жизни облачной ячейки [6, 7].
Согласно этой теории, по мере увеличения ядер кристаллизации увеличиваются осадки, затем наступает максимум, после которого количество осадков снижается. Именно в этой зоне условия образования и роста града становятся менее благоприятными.
Таким образом, представляется, что из теории образования осадков следует наличие звена, воздействуя на которое можно изменить ход процесса роста облачных элементов (кристаллов, капель, града). Это звено – количество ядер кристаллизации. Регулируя этот показатель и имея ввиду ограниченность энергетического ресурса данного термодинамического процесса, мы можем влиять на его развитие.
В рамках этого механизма и для конвективных, и для слоистых облаков были построены три основные методики введения ядер кристаллизации в область осадкоообразования, зарождения и роста града, в том числе – с помощью самолётов, снарядов или ракет и наземных генераторов.
При этом главные отличия этих методов заключаются в том, что по разному определяются место и стадия развития облачной ячейки для оптимального введения ядер кристаллизации. Для всех этих методов имеется и общее условие. Число искусственных ядер кристаллизации на уровне их активности, т.е. при температуре минус 4 – минус 5 градусов должно быть для увеличения осадков не менее чем 102–103 на кубометр, а для предотвращения образования и роста града – не менее чем 105–106 на кубометр (чем больше – тем лучше).
Для достижения максимального эффекта чрезвычайно важно относительно точное определение места воздействия в облачной ячейке и стадии её развития. Не останавливаясь здесь на этих способах решениях этих задач, отметим лишь, что они весьма сложны, но от их правильного решения зависит успех воздействия.
С учётом этого обстоятельства, простой способ решения этих задач, возможно, содержится в наземном способе засева. В этом случае сам процесс облакообразования и локализация областей осадко- и градообразования проходят с участием генерируемых у земли искусственных ядер. Вертикальными потоками, формирующими конвективные ячейки или области максимальной активности образования осадков в слоистых облаках, эти искусственные частицы могут переноситься в нужное место и в нужное время. Если это так, то важно обеспечить генерацию такого количества ядер кристаллизации на определенных уровнях, которое требуется для эффективного воздействия на процесс образования осадков или града.
Возможно, существуют ситуации и процессы, когда засев может быть выполнен наземными средствами, что позволило бы избежать более дорогостоящих и сложных в организации способов доставки реагентов.
Можно выделить три механизма вертикального переноса частиц в подоблачном слое:
1. Турбулентная диффузия частиц в подоблачном слое.
2. Восходящие конвективные струи, возникающие за счет тепловыделения в генераторе частиц.
3. Естественные конвективные движения (в частности, конвективные ячейки в пограничном слое атмосферы).
Ниже содержатся расчеты и оценки, относящиеся к этим механизмам.
1. Турбулентная диффузия частиц
Решения уравнений диффузии в простейших случаях известны; из них вытекает, что область, куда успели продиффундировать частицы, расширяется со временем t примерно как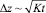 
, где K – коэффициент диффузии. Если принять значение коэффициента турбулентного обмена K = 10 м2/с м2/с, то через 3 часа Δz ~ 300 м. Даже если принять K = 10 м3/с м2/с (для данных масштабов – заведомо завышенное значение), то через час Δz ≤ 2000 м. Поэтому в рассматриваемом контексте «чистая» диффузия без учета конвекции представляется неэффективным механизмом переноса.
2. Восходящие конвективные струи
2.1. Модель турбулентных конвективных струй
Сделаем оценку подъема частиц за счет конвекции, возникающей вследствие тепловыделения в генераторе. Сначала будем рассматривать ситуации, когда фоновый горизонтальный перенос несуществен. Будем пользоваться численной моделью восходящих турбулентных конвективных струй, которая подробно описана и проанализирована в [4]. В упомянутой монографии эта модель в какой-то мере апробирована сопоставлением с натурными данными (но следует оговориться, что эта модель разработана и проверена для случаев значительно более мощных источников тепла, чем в рассматриваемых нами генераторах частиц). Приведем некоторые сведения об используемой модели.
В теории струй метеотронов обычно предполагается, что на некотором уровне z = 0 действуют стационарные источники тепла и вертикального количества движения мощностью Qθ и Qw соответственно, локализованные в одной и той же области малых размеров. Предполагается, что мощность этих источников достаточно велика, так что над ними образуется относительно тонкая турбулентная осесимметричная восходящая струя. Но роль источника количества движения с высотой обычно быстро убывает даже в случае мощных струй, генерируемых реактивными двигателями [4]. В нашем случае, тем более, в качестве источника вертикального движения рассматриваем только тепловыделение в генераторе частиц.
С использованием приближения пограничного слоя, вытянутого вдоль оси струи и гипотезы подобия профилей вертикальной скорости и температурного возмущения в струе, для этих возмущений температуры и скорости выведена система уравнений
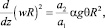(1)
(2)
Здесь z – вертикальная координата; R(z) – радиус струи (эта функция определяется интенсивностью вовлечения); w и θ – вертикальная скорость и отклонение температуры на оси струи соответственно; α = 1/T* – термический коэффициент расширения воздуха; T* – средняя температура в рассматриваемом слое воздуха; g – ускорение свободного падения; Γ(z) = γa – γ(z) – отличие вертикального градиента температуры от сухоадиабатического (Γ > 0 соответствует устойчивой стратификации); ai – безразмерные коэффициенты, значения которых выражаются через интегралы от предполагаемых радиальных профилей w и θ. В [4], из эмпирических данных приняты радиальные зависимости типа 
, для которых a1 = a3 = 1/4, a2 = a4 = 1/3.
Напомним физический смысл системы (1), (2). Величина (wR)2 пропорциональна вертикальному количеству движения элемента струи, произведение αgθR2 – работе, совершаемой силами плавучести при подъеме элемента струи. Эта работа и приводит к изменению с высотой количества движения. Аналогичным образом, теплосодержание элемента струи (относительно окружающей среды) wθR2 меняется с высотой пропорционально Γw, поскольку в процессе его подъема меняется температура окружающей его среды. Рассматриваемая модель (дифференциальная) мало отличается от известных интегральных моделей (например, [11]). Отметим, что при выводе уравнений (1), (2) предполагалось, что струя вытянута по вертикали. Поэтому они могут существенно нарушаться, например, в области горизонтального растекания струи под задерживающим слоем, а также непосредственно над источником, где еще не сформировалась четко выраженная струя.
Аналогичное (2) уравнение можно вывести и для влажности воздуха (эффекты влажности пока не учитываем) и для других примесей. Например, если примесь консервативна и фоновый градиент ее концентрации n отсутствует, то уравнение ее переноса в данном приближении представляет собой просто закон сохранения ее потока вдоль сечения струи:
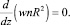(3)
Из (3) следует
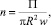(4)
где Π – поток примеси через сечение струи, который можно считать известным, зная параметры генератора частиц. Таким образом, для расчета изменений в струе концентрации частиц, необходимо знать зависимости R(z), w(z).
Соотношение (4) вполне прозрачно и может быть обобщено на более общий случай, когда имеется и горизонтальный перенос, так что струя не вертикальная, а наклонная. Если понимать под абсолютное значение скорости (не обязательно вертикальной) вдоль оси струи, то объем элемента струи равен Sw, где S = πR2 – площадь поперечного сечения струи. Именно в этом объеме распределяются частицы, генерируемые источником за единицу времени. Отсюда понятна справедливость соотношения (4) практически для любых струй, а не только для свободной конвекции над источником тепла. Но радиус струи R и скорость для струй разной природы могут, вообще говоря, очень различно зависеть от высоты или от координаты вдоль струи.
В литературе можно встретить сведения, о том, что льдообразующие частицы в действительности не являются консервативной примесью, в частности, они могут дезактивироваться, либо, наоборот, активироваться под влиянием солнечного излучения (см., например, [1, 9, 10]). Эти сведения к настоящему времени весьма противоречивы. Ниже выполнены расчеты как для случая консервативных частиц, так и с учетом возможности их несохранения.
Если считать фоновый профиль Γ(z) известным, то уравнения (1), (2), вообще говоря, представляют собой систему двух уравнений с тремя неизвестными w, θ, R (дополнительное включение уравнения (3) добавляет одно уравнение и одно неизвестное). Для замыкания системы требуется привлечение дополнительной информации или гипотез. Нередко используется гипотеза о вовлечении, пропорциональном периметру сечения струи (т.е. ее радиусу R(z)) и вертикальной скорости [12]. Иными словами, вовлечение предполагается пропорциональным площади боковой поверхности элемента струи 2πRw. Тогда можно записать третье уравнение, которое замыкает систему [12]. В [4] используется более простая схема: на основе теоретических соображений и опытных данных принимается, что радиус турбулентной струи линейно возрастает с высотой:
R(z) = βz, (5)
где значение безразмерного коэффициента β находится в пределах 0,1–0,2. Ниже для конвективных струй будет использоваться такая гипотеза замыкания.
Рассмотрение точечных источников на нижнем уровне z = 0 сопряжено с некоторыми трудностями для численного моделирования. Эти трудности в большой степени носят формальный характер, поскольку известно, что динамика струй от локальных источников вдали от них мало зависит от деталей геометрии этих источников – она определяется лишь интегральными интенсивностями источников тепла и количества движения. Поэтому задачу можно регуляризировать – заменить точечные источники источниками конечного радиуса R = Rs, находящимися на некоторой малой высоте z = zs. Конкретные значения zs и Rs (связанные между собой соотношением (5) при этом нередко несущественны – с высотой струя быстро «забывает» об этих значениях, и решения практически не зависят от них.
2.2. Результаты расчетов
Интенсивность свободновосходящей конвективной струи определяется, прежде всего, интенсивностью источника тепла Qθ = Q. В данном случае Q ~ 104 Вт. (Эта цифра получается следующим образом. Теплотворная способность топлива не превышает по порядку величины 3·107 Дж/кг – столько у спирта; у нефтепродуктов лишь в полтора раза больше. Если сгорает порядка 1 кг в ч, то и получается Q ~ 104 Вт). На рис. 1 приведен пример зависимости скорости восходящих движений на оси струи w(z) от вертикальной координаты z при указанной интенсивности тепловыделения и слабонеустойчивой стратификации (отличие от сухой адиабаты Γ = –10–4 К/м).
Скорость восходящих движений сначала (на нижних сотнях метров) получается небольшой, поскольку интенсивность тепловыделения в генераторе частиц в тысячи раз меньше, чем в случае метеотрона или двигателя большого судна (при нейтральной стратификации w ~ Q1/3 [4, 12, 11]). Но затем становится существенной неустойчивая стратификация, которая постепенно становится основным источником энергии струи, так что струя, хотя и медленно, ускоряется с высотой. Как можно проверить прямой подстановкой, система уравнений (1), (2), (5) при неустойчивой фоновой стратификации Γ < 0 имеет решение, не зависящее от интенсивности источника:
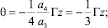
(6)
где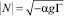 
. На эту линейно растущую с высотой асимптотику и выходит рассчитанный численно профиль вертикальной скорости, представленный на рис. 1. При Γ = –10–4 К/м К/м 
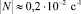. Согласно натурным данным, предполагаем, что изотерма –6 °С находится на уровне 4 км. На этой высоте в струе w ≈ 2,5 м/с м/с, θ ≈ 0,1 к К.
Рис. 1. Пример профиля вертикальной скорости в восходящей конвективной струе над генератором
Подобные решения были ранее известны для близких задач. Например, решение для «спонтанного термика» в книге Гутмана [5] отличается от (6) лишь численным коэффициентом (в [5] рассматривается не турбулентная, а квазиламинарная струя с K = const, так что некоторое различие коэффициентов не удивительно).
Пусть А – интенсивность расхода йодистого серебра (г/с), р – количество частиц, которое дает каждый грамм (1/г). Тогда, количество частиц, генерируемое за единицу времени, будет Π = Ap (1/с). Если A = 8,88,8 г AgI в час ≈ 3·10–3 г/с; p ≈ 2·1014 1/г, то Π = 6·1011 1/с. На высоте 4 км, где w ≈ 2,5 м/с, R = 600 м (при β = 0,15), согласно (4), получаем концентрацию частиц n ≈ 2·105 1/м3 на площади, порядка площади поперечного сечения струи – около 1 км2. Если до рассматриваемого уровня доходят не все частицы (учитывается достаточно сильная дезактивации реагента при подъёме под воздействием солнечных лучей), а, например, лишь одна из двадцати, то n = 104 1/м3. На рис. 2 приведена вертикальная зависимость концентрации частиц в восходящей струе (без поправки на потери частиц). С учетом асимптотики (6), эту зависимость на уровнях выше километра можно приближенно выразить аналитически:
(7)
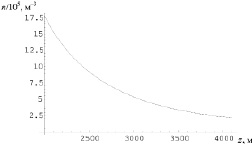
Рис. 2. Вертикальная зависимость концентрации частиц в восходящей струе (в 1/м3) для рассмотренного численного примера
Использованная выше модель восходящей конвективной турбулентной струи является весьма идеализированной. В свое время она была апробирована для интенсивных струй (метеотронов), в которых турбулентность много интенсивнее фоновой. В данном случае струя довольно слабая, а модель, как упоминалось, учитывает только турбулентность, генерируемую струй, т.е. не учитывает фоновую турбулентность, которая в данном случае может преобладать. Другой важный неучтенный выше негативный фактор – фоновый горизонтальный перенос.
2.3. Оценка времени подъема
Выше уровня 1 км, на участке линейного роста функции w(z) (рис. 1) можно в лагранжевых переменных записать
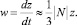
Интегрируя последнее уравнение, получаем закон движения лагранжевой частицы:
(индекс 0 относится к некоторому начальному уровню рассматриваемого интервала, например, к уровню z = 11 км). Отсюда следует, что характерное время преодоления слоя z > 11 км порядка часа.
В нижнем слое 1 км скорость восходящих движений на всех уровнях не ниже 0,5 м/c, подъем до уровня 1 км занимает, во всяком случае, менее 1·103 с ~ 0,5 час. Таким образом, при рассмотренной выше очень слабой неустойчивости общее время подъема получается порядка 1 часа. В нижеследующих расчетах, учитывающих более интенсивные естественные конвективные движения при более неустойчивых стратификациях, время подъёма частиц может существенно уменьшаться.
2.4. Учет активации и дезактивации льдообразующих частиц
Как уже указывалось, в литературе имеются весьма противоречивые сведения о возможной степени активации и дезактивации льдообразующих частиц в процессе их распространения в атмосфере.
Согласно данным [1], с момента сжигания реагента в ацетоне в течение первых 300 с, число льдообразующих ядер увеличивается под влиянием солнечной радиации в 50 раз. В первом приближении это эквивалентно увеличению в 50 раз интенсивности источника частиц Ap (как указывалось выше, для струи существенна общая интенсивность источника, а не детали распределения этого источника). В последующий час, по данным [1], преобладает процесс дезактивации ядер; будем предполагать, что их число за час уменьшается в 100 раз. В итоге, в приведенном численном примере концентрация частиц на уровне изотермы –6 °C уменьшается в два раза и составляет порядка 105 1/м3. Таким образом, при указанных предположениях порядки величин не меняются и с учетом несохранения количества льдообразующих частиц. В нижеследующих расчетах время подъема обычно составляет меньше часа. Поэтому поправка на потери частиц будет ещё меньше, чем в приведенном примере.
3. Перенос частиц естественной конвекцией и адвекцией
Естественная атмосферная конвекция может, вообще говоря, существенно интенсифицировать вертикальный перенос льдообразующих частиц. Наличие весьма интенсивных вертикальных движений в нижней атмосфере при неустойчивой стратификации и их влияние на перенос примеси анализируется, например, в монографиях [2, 3]. На рис. 3 приведен заимствованный из [3] пример сглаженной реализации вертикальной скорости на уровне 120 м.
Рис. 3
С высотой восходящие движения в рассматриваемых условиях в подоблачном слое обычно лишь усиливаются. Пусть, например, область естественных восходящих движений проходит через генератор частиц в течение времени τ. За это время в область восходящих движений попадает Apτ частиц. Обозначим через W среднюю скорость восходящих движений. Тогда частицы преодолеют слой толщиной Δz за время порядка T = Δz/W. Оценим концентрацию частиц по прошествии этого времени T, т. е. на уровне Δz. Это зависит, в частности, от геометрии облака частиц.
Пусть область восходящих движений (конвективная ячейка) проходит по горизонтали над генератором с характерной горизонтальной скоростью приземного ветра U. Тогда попавшие в воздух за время τ частицы будут, в основном, распределены вдоль линии длиной Uτ (иными словами, вниз по потоку образуется горизонтальная струя этих частиц). В процессе подъема частиц будет происходить их диффузия, которая, в основном, существенна в направлении, поперечном к оси этой струи (т.е., речь идет о расширении упомянутой горизонтальной струи за счет турбулентной диффузии). Предполагаем, как обычно, что закон диффузии: 
. В процессе расширения области, содержащей частицы, ее объем (объем тела типа цилиндра длиной Uτ, радиусом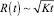 
) можно оценить как 
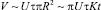. За время подъема этот объем достигнет значения 
, а концентрация частиц (без учета дезактивации):
(8)
Интересно отметить, что последнее выражение не зависит от τ – времени прохождения области восходящих движений через генератор. Это понятно, поскольку количество частиц, попавших в воздух, на единицу длины упомянутой горизонтальной струи, при прочих равных условиях не зависит от τ. Но от этой величины зависит длина поднимающегося горизонтального участка струи и, следовательно, полное количество поднимающихся частиц.
Примем для численной оценки следующий набор значений параметров: τ = 5 мин (предполагаем, что генератор недолго находится в области восходящих движений), W = 1 м/с (средняя скорость восходящих движений относительно невелика), Δz = 4 км, K = 10 м2/c, U = 5 м/с. Как и прежде, предполагаем A = 8,8 г AgI в час ≈ 3·10–3 г/с, p ≈ 2·1014 1/г. Время подъема T = Δz/W получается около часа, длина горизонтальной струи, в которой распределены частицы, Uτ – около 1,5 км. Радиус струи (области распределения частиц) за время подъема расширяется до значения R ≈ 200 м; V ≈ 107 м3. Тогда концентрация частиц на уровне Δz = 4 км – порядка 106 1/м3. Но следует иметь в виду, что, ввиду наличия горизонтального переноса, частицы достигнут этого уровня на горизонтальном расстоянии около 20 км вниз по потоку от источника. Горизонтальный перенос льдообразующих частиц, возможно, является наиболее серьезной проблемой для рассматриваемой технологии. Кроме того, на временах порядка часа, возможно, следует принимать большие значения эффективного коэффициента турбулентного обмена K, а концентрация, согласно (8), обратно пропорциональна этой величине.
Следует также иметь в виду, что приведенная выше схема подъема, вообще говоря, упрощена. Подъем частиц естественной конвекцией в природе может складываться из различных этапов. Прежде, чем частицы будут захвачены и подняты восходящими движениями конвективного облака, они могут в пределах пограничного слоя переноситься мелкой конвекцией (ячейки типа Рэлея-Бенара). А прежде, чем попасть в упомянутые ячейки, на нижних десятках метров они могут подниматься, благодаря турбулентной диффузии в приземном слое и тепловыделению в генераторе. Теории, надежно описывающей эффективность перехода частиц от одних упомянутых типов движений к другим в настоящее время, насколько нам известно, нет.
В приведенной выше численной оценке предполагалось, что характерная скорость подъема частиц составляет 1 м/с. Но имеются и более благоприятные ситуации с подъемом, значительно более быстрым. В таких случаях льдообразующие частицы меньше успевают рассеяться и в меньшей степени уносятся по горизонтали. Согласно современной методике расчетов, максимальная скорость восходящего потока, равна половине квадратного корня из удвоенного значения CAPE (convective available potential energy). Если последнее, например, равно 200 Дж/кг (а оно нередко бывает и в несколько раз больше), то скорость подъема получается уже порядка 10 м/с. Время подъема и горизонтальный перенос в этом случае будет в 10 раз меньше приведенной выше оценки, а концентрация частиц – в 10 раз больше.
К этому следует учесть, что процесс распространения примеси в объёме облачной ячейки (в данном случае льдообразующих аэрозолей) на стадии осадкообразования (роста капель или градин) происходит очень быстро. Выполненные с помощью трассеров специальные эксперименты показали, что при вводе их на начальной стадии развития процессов осадкообразования они обнаруживаются по всей площади осадков, выпавших из этой ячейки [8].
4. Модель восходящей струи при наличии горизонтального переноса
Выше были рассмотрены некоторые простейшие ситуации. Попытаемся также сделать оценки для некоторых более сложных геометрий.
Ниже (рис. 4) схематически изображена струя частиц от генератора, сносимая ветром и поднимающаяся (причина подъема здесь не принципиальна – это может быть как источник тепла в генераторе, так и естественная конвекция при наличии также и горизонтального переноса). В отличие от раздела 2, струя частиц в данном случае не обязательно конвективная – даже за холодным источником частиц вниз по течению тянется «струя» частиц.
Обозначим через v скорость вдоль струи (она векторно складывается из горизонтального ветра и вертикальной конвекции)), а через s ≈ vt – координату вдоль струи.
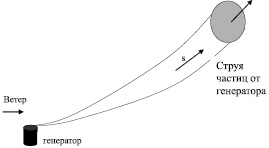
Рис. 4. Схематическое изображение струи с частицами, всплывающей на фоне горизонтального ветра (вид сбоку)
Радиус сечения струи
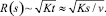
Поток частиц через каждое сечение струи в известном приближении одинаков и равен мощности источника Π:
(9)
(n – концентрация частиц). Отсюда следует простая, но довольно общая формула:
(10)
Например, если струя поднялась на нужную высоту на расстоянии 20 км от генератора, то s ≈ 20 км; если при этом Π = 6·1011 1/с, K = 10 м2/с, получаем n ≈ 106 1/м3. Даже если принять очень большое значение K = 103 м2/с, то n ≈ 104 1/м3. Причем, площадь поперечного сечения струи растет пропорционально K. Поэтому, хотя с ростом K падает концентрация, но общее число поднимающихся частиц не меняется. Это и понятно, поскольку если струя всплывает до уровня необходимых изотерм, то, на этот уровень попадают все частицы, независимо от значения K.
Интересно отметить, что результат (10) не зависит явно от скорости переноса v, а зависит от пройденного пути s. С ростом скорости струя меньше успевает расшириться на фиксированном участке пути, но зато растет длина элемента струи, так что его объем, как и концентрация остаются неизменными. Таким образом, соотношение (10) выглядит не только простым, но и надежным. Но оно не содержит информации о факте подъёма струи – концентрация при прочих равных условиях одинакова и для струй, попавших в область восходящих движений, и для случая чисто горизонтального переноса. Поэтому дополнительно приходится предполагать достаточную вероятность попадания струи в область интенсивных восходящих движений.
5. Предварительное внесение частиц в приземный слой «цепочкой» генераторов
До сих пор рассматривалось распространение частиц от одного генератора или локализованной группы генераторов. Один из недостатков такой геометрии состоит в следующем. Конвекция, вызываемая тепловыделением самих генераторов, слабая. Если же полагаться на естественные восходящие движения, то, даже если «корни» облаков проникают относительно близко к подстилающей поверхности, то кажется вполне возможным, что генераторы окажутся где-нибудь в стороне от восходящего движения – на другой вертикали. Иными словами, неясно, насколько вероятно частицам из генератора попасть именно в область интенсивного восходящего движения. А это в оценках фактически предполагалось.
Как представляется, в принципе, существует альтернатива – пытаться предварительно распределять частицы в больших горизонтальных областях приземного/пограничного слоя более или менее равномерно (горизонтальный ветер и сильная турбулентность этому даже способствуют). И тогда естественные интенсивные восходящие движения, на какой бы вертикали они не возникали, будут подхватывать частицы с большой вероятностью.
Рассмотрим в этой связи модель «цепочки» генераторов, вытянутой примерно поперек горизонтального ветра Вид сверху:
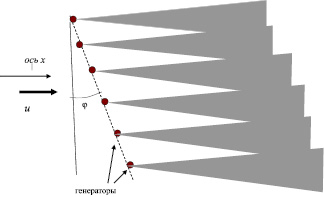
Рис. 5. Схема воздействия с использованием «цепочки» генераторов частиц (вид сверху)
За каждым генератором тянется вниз по потоку расширяющаяся горизонтальная струя частиц. На некотором расстоянии вниз по потоку эти струи сливаются, образуя примерно однородное распределение частиц в приземном/пограничном слое. Оценим, на каком расстоянии струи будут сливаться, и какая будет концентрация частиц в приземном/пограничном слое.
Пусть цепочка генераторов расположена перпендикулярно ветру (поправка на возможное наличие некоторого угла, обозначенного на рисунке через φ, делается легко и даже приводит к увеличению концентраций частиц). Обозначим через u скорость горизонтального ветра, через d – расстояние между генераторами. Предполагаем, что горизонтальные струи расширяются по диффузионному закону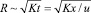 
(строго говоря, надо различать коэффициенты горизонтального и вертикального турбулентного обмена). Тогда струи будут сливаться через «лагранжево» время Δt порядка d2/K на расстоянии порядка Δx = ud2/K вниз по потоку. Если d = 300 м, K = 100 м2/c, u = 5 м/с, то Δt ~ 103~103 с, Δx ~ 5 км. Ниже по потоку частицы будут распределены относительно однородно по горизонтали в слое толщиной h порядка 
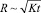. При Δx ~ 5 км имеем h ~ 300 м.
Обозначим производительность одного генератора через Π (частиц/c). После слияния струй частицы, испущенные одним генератором в единицу времени будут в среднем приходится на объем порядка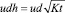 
. Следовательно, концентрация частиц в слое толщиной h будет
где x – расстояние вниз по потоку от цепочки генераторов. С удалением от генераторов концентрация, естественно, убывает, поскольку частицы распределены хотя и однородно по горизонтали, но в слое, толщина которого возрастает вниз по потоку. При x = Δx (на том удалении, где струи сливаются), имеем
Отметим, что последнее соотношение не зависит от K и, тем самым, дает возможность для весьма надежных оценок.. Если, по-прежнему считаем Π = 6·1011 1/с, то при рассматриваемых значениях параметров последнее соотношение дает n ≈ 106 1/м3. Такова будет концентрация на больших площадях в слое толщиной порядка d = 300 м (вниз по потоку она постепенно уменьшается, но зато охватывает все более толстый слой). Если генераторы в цепочке располагать чаще, то можно добиться и значительно более высоких концентраций.
Если интенсивные естественные восходящие движения «задевают» этот слой (например, в этот слой проникают «корни» интенсивных облаков), то можно предположить, что в благоприятных случаях указанные концентрации без больших потерь могут переноситься на необходимые уровни. Например, при скорости восходящих движений 10 м/с уровень 4 км достигается за несколько минут. Даже при K = 100 м2/с диффузионное «расплывание» за это время составляет всего порядка 200 м. Тогда объем воздуха таких и больших линейных размеров за время подъема из приземного слоя сильно не перемешается, и объемы воздуха из пограничного слоя с упомянутыми концентрациями достигнут уровня –5 град.
Модель для такой геометрии воздействий содержит меньше спорных упрощающих предположений, чем некоторые модели конвективных струй и в этом отношении представляется надежнее.
7. Возможные резервы для усиления эффекта
1. Увеличение числа генераторов в точке и количества реагента, сжигаемого в единицу времени
В моделях ряда предыдущих разделов достигаемая концентрация частиц пропорциональна интенсивности источника Ap. Поэтому увеличение числа генераторов в точке или в горизонтальном ряду и количества реагента, сжигаемого в единицу времени, должны приводить к пропорциональному увеличению концентрации частиц. На времени подъема частиц это в большинстве случаев существенно не сказывается.
В случае механизма, связанного с искусственными струями, возникающими над генераторами, в приведенных расчетах бóльшая часть пути, проходится струей за счет энергии неустойчивости среды. При этом справедлива формула (7), т.е. это пример случая, когда достигаемая концентрация частиц растет пропорционально числу генераторов в точке и количеству реагента, сжигаемого в единицу времени. На начальной стадии струи (нижние сотни метров, когда струя еще не вышла на «спонтанный» режим) положительный эффект такого увеличения даже несколько сильнее – с интенсивностью источника тепла еще и увеличивается скорость подъема (но этот эффект не сильный – как уже упоминалось, при нейтральной стратификации вертикальная скорость пропорциональна корню кубическому из интенсивности источника тепла).
2. Увеличение количества генераторов, распределенных на данной территории и увеличение размеров территории
Перенос частиц естественной конвекцией сильно зависит от того, находится ли генератор в области восходящих движений, которые обычно охватывают меньшую часть площади. Поэтому увеличение количества генераторов на данной территории пропорционально увеличивает количество генераторов находящихся в данный момент в области восходящих движений. Пропорционально увеличивается и количество частиц, захватываемых восходящими движениями и достигающих необходимого уровня.
Если генераторы размещены на достаточно большой территории (с горизонтальными размерами в несколько десятков километров), то можно добиться того, что поднимающиеся частицы, несмотря на достаточно сильный горизонтальный перенос, будут достигать уровня изотермы –6 °С над заданной территорией.
3. Увеличение продолжительности работы генераторов
Увеличение продолжительности работы генераторов пропорционально увеличивает продолжительность времени, в течение которого каждый генератор находится в области восходящих движений. Поэтому эффект аналогичен упомянутому выше случаю увеличения количества генераторов.
4. Учет и использование орографических эффектов
Частицы от генераторов, расположенных высоко над уровнем моря, при прочих равных условиях могут заметно быстрее достигать необходимого уровня. В еще большей степени этому могут способствовать восходящие движения воздуха орографического происхождения.
Пусть, например, угол наклона подстилающей поверхности к горизонту φ = 20°. Если скорость горизонтального ветра U = 10 м/с, то скорость подъема частиц от генераторов, расположенных на подветренной стороне склона может достигать Utgφ ≈ 3,5 м/c, и уровень 4 км может достигаться льдообразующими частицами за время порядка 20 мин.
5. Некоторые рекомендации по использованию результатов настоящего исследования в практических целях
Исходя из приведенных расчётов, граничные условия состояния тропосферы, при которых наземные генераторы могут быть эффективны для увеличения осадков и предотвращения опасного для сельскохозяйственных культур града, должны устанавливаться на базе особенностей развития осадкообразовательного процесса каждого региона отдельно.
Общими для всех регионов необходимыми условиями являются неустойчивое состояние атмосферы со скоростью восходящего потока не менее 1 м/с и достаточной, для поднятия льдообразующих аэрозолей, турбулентностью в приземном слое атмосферы до уровня корней естественной конвекции (нескольких десятков метров).
Учитывая пульсации вертикальных скоростей даже до минусовых значений (см. рис. 3), целесообразно наземные генераторы поднимать на несколько метров над землёй, что бы исключить влияние слоя шероховатости. Можно предположить, что в момент отрицательного импульса аэрозоли могут опускаться до слоя шероховатости и оставаться в нём.
Некоторые рекомендации для разработки технологии этих работ мы можем дать на основании исследований засева различных типов облаков с помощью ракет и самолётов, выполненных в Молдавии и в Украине [6, 7]. Принимаем, что для воздействия льдообразующих реагентов на осадкообразовательные процессы в облаке не имеет значение каким путём они были туда доставлены. Важно, что бы он попал в зону осадкообразования на начальной стадии процесса и в нужном количестве. Засев гродоопасных облаков должен начинаться в тот период, когда в облаке ещё только начинается процесс зарождения и роста града [6].
Для увеличения осадков из облаков слоистых и слоисто кучевых форм следует придерживаться следующих условий.
Засев следует начинать при обнаружении в облачной системе пригодных для засева слоев.
Заметим, что в задачах увеличения осадков эти критерии отличаются для облаков, дающих естественные осадки (Ns – As), и облаков, из которых осадки не выпадают (Sc, St, Ac). Облачные системы, дающие естественные осадки (Ns – As), считаются пригодными для засева в тех случаях, если в них имеются капельные или смешанные по фазовому строению слои любой толщины (от 50 м и более) при температуре минус 4 °С и ниже. Облака Sc, St, Ac, из которых осадки не выпадают считаются пригодными для засевов с целью увеличения осадков тогда, когда они имеют капельное строение, температуру не выше минус 4 °С, толщину не менее 500 м, а нижнюю границу не выше 1000 м. Для Ac толщина облаков должна была быть более 600 м. Для зимних внутримассовых облаков слоистых (St) и волнистых (Sc, Ac) форм дополнительным критерем может быть данные о водозапасе более 30 г/м2.
Продолжительность воздействия должна соответствовать длительности сохранения пригодных для засева облаков. При засеве Sc, St, Ac протяженность зоны увеличения осадков от точки попадания реагента в облако может соответствовать переносу за 45 мин. (20–30 км).
Для увеличения осадков из облаков конвективных форм следует придерживаться следующих условий.
Засев конвективной облачной ячейки в ряде случаев может приводить к увеличению количества осадков, а в ряде случае к их уменьшению. В выполненном в Молдавии многолетнем эксперименте [6, 7] в результате засева относительная частота повторения очень слабых и слабых ливней уменьшилась под влиянием засева на 19 и 54 % соответственно. Наиболее вероятной причиной этого результата является интенсификация такого типа облаков под влиянием засева и переход их в более активную стадию. В то же время существенно возросла частота повторения умеренных (на 121 %), значительных (на 58 %) и сильных (на 25 %) ливней. Частота очень сильных ливней осталась практически неизменной, а частота появления особо опасных ливней под влиянием засева уменьшилась вчетверо. Соответственно изменился и режим осадков. Масса осадков уменьшилась в группе очень слабых ливней на 8 %, в группе слабых ливней на 51 % и увеличилась в группах умеренных (на 75 %), значительных (на 55 %) и сильных (на 52 %) ливней. В группах очень сильных и особо опасных ливней вновь отмечено уменьшение массы осадков на 17 и 80 % соответственно.
Увеличение осадков при засеве отмечается только в том случае, если он совпадает с периодом развития облачной ячейки и, наоборот, приводит к обратному эффекту, если он совпадает с периодом её диссипации. Исключение, по данным экспериментов, составляют очень слабые облачные ячейки, развивающиеся в условиях слабой конвекции. Засев большим количеством реагента (105–106 льдообразующих ядер на м3 облачного объёма) таких ячеек в ряде случаев приводит к их разрушению. Интенсификация осадкообразующего процесса в облаках, дающих очень сильные и опасные ливни приводит к их ускоренному разрушению и соответственно к уменьшению осадков из них. Для получения максимального количества осадков из конвективных облаков за сезон воздействия не следует засевать облачные ячейки дающие при естественном развитии очень сильные и особо опасные ливни (распределение ливней по категориям см. [6]. Знак и величина эффекта воздействия на облачную ячейку – сложная функция её состояния и термодинамических условий развития в момент засева. В то же время для предотвращения роста опасного по размерам града все категории ячеек следует засевать предельно возможным количеством льдообразующих аэрозолей и начинать засев как можно раньше, т.е. на начальной стадии роста градовых частиц.
В момент диссипации осадкообразовательного и градообразовательного процесса работа наземных генераторов не целесообразна и их следует выключать. Исключением составляют процессы, когда диссипация облаков за счёт динамики фронтов или солнеченого прогрева сменяется на их рост.
Практическая реализация этих условий может быть решена путём существующих способов сверхкраткосрочного (заблаговременность полчаса – час) прогноза развития облачных процессов с помощью анализа синоптических карт, радиозондов, а так же параметров облаков, получаемых с помощью радиолокаторов [6].
Как показали наши расчёты при скорости восходящих потоков 1м/c, значении CAPE 200 Дж/кг в задачах увеличения осадков заблаговременность для принятия решения о засеве и включение наземных генераторов достаточна полчаса. При горизонтальной скорости ветра 20 км/ч зона предварительного засева должна составлять не менее 20 км. При скорости восходящих потоков больших 1м/c заблаговоременность включения генераторов может быть уменьшена.
Учитывая не учтенённые в расчётах возможные механизмы горизонтального рассеяния реагента, пульсации вертикальной скорости в нижнем приземном слое (см. раздел 3, рис. 3 нашей статьи), другие причины уменьшения его концентрации и дезактивации, в задачах предотвращения роста града следует начинать работу всех генераторов (см. параграфы 6.1–6.4) ни менее чем за час до развития градоопасных облаков. Точное время заблаговоременности включения и количества одновременно работающих генераторв, длина зоны предварительного засева с учётом розы ветров должна определяться экспериментально для каждого региона отдельно.
Заключение
Рассмотренные выше модели переноса льдообразующих частиц от наземных генераторов нередко дают при неустойчивой стратификации атмосферы довольно высокие их концентрации на уровнях изотерм –5...–6 °С (до 106 частиц/м3). Такие концентрации могут достигаться при скорости подъёма воздуха 1 м/с примерно через час с начала работы генератора.
При интенсивных осадкообразовательных процессах энергия неустойчивости в приземном слое воздуха может достигать 200 Дж/кг, а нередко бывает и в несколько раз больше. Скорость подъема воздуха при этом получается уже порядка 10 м/с. (В Молдавии градобития, к примеру, бывают при наличии вертикальных скоростей 18 м/с и более). Время подъема и горизонтальный перенос в этом случае могут быть значительно меньше, а концентрация частиц – больше. Например, при скорости восходящих движений 10 м/с уровень 4 км достигается частицами за несколько минут. При коэффициенте турбулентности K = 100 м2/с диффузионное «расплывание» за это время составляет всего порядка 200 м.
Регулируя время, интенсивность работы наземных генераторов, их количество и расположение на местности можно эффективно использовать этот метод и для работ по увеличению осадков, и для предотвращения роста града.
При некоторых геометриях расположения генераторов модели содержат относительно немного спорных упрощающих предположений. Таким образом, не исключается возможность того, что такой путь воздействий может быть эффективным. При этом отпадает необходимость радиолокационного определения места в облаке для его засева в задачах увеличения осадков и предотвращения роста града. Льдообразующие частицы находят это место сами, участвуя в естественном процессе облако- и осадкообразования.
Библиографическая ссылка
Диневич Л.А., Ингель Л.Х., Хаин А. Оценки переноса льдообразующих частиц от наземных генераторов // Современные наукоемкие технологии. – 2013. – № 2. – С. 14-25;URL: https://top-technologies.ru/ru/article/view?id=31323 (дата обращения: 21.11.2024).