Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Снежин А.Н. 1 Петров С.В. 1

---

1 ООО «Газпром развитие»

Наиболее актуальной и сложной проблемой, стоящей перед потоковыми комплексами, является задача о распределении потоков. При вводе ограничений пропускной способности и управляющих воздействий эта задача по определению становиться задачей управления потоками, включающая в себя сразу несколько типов потоковых задач – транспортные задачи, задачи определения существования потока, задачи о поиске обобщенного потока и пр. В статье «Алгоритм управления распределением потоков газа в замкнутой газотранспортной системе» была представлена оригинальная математическая модель и реализующий ее метод расчета оптимального распределения потоков газа в сложной замкнутой системе газопроводов без учета значений ГИС. Также в ней была представлена полученная в ходе разработки метода теорема о решении на реверсивных дугах. В настоящей статье приводится доказательство выдвинутой теоремы и разбирается решение задачи управления распределением потока газа с реверсивными дугами и с учетом значений ГИС.

Статья в формате PDF

3374 KB

математическая модель; теорема; доказательство; распределение потоков газа; реверсивный газопровод; газо-измерительная станция (ГИС); газотранспортная система (ГТС); товарно-транспортная работа (ТТР)

1. Казак А.С., Русакова В.В., Кудрявцев И.Б., Ратнер Д.А., Кудрявцев А.А. – Обоснование оптимальных вариантов развития и реконструкции газотранспортных систем в условиях неопределенности, – М.: Газпром ВНИИГАЗ, 2010. – 188 с.

2. Карманов В.Г. Математическое программирование: учеб. пособие. – 5-е изд., стереотип. – М.: ФИЗМАТЛИТ, 2004. – 264 с.

3. Кармен Т.Х., Лайзерсон Ч.Е., Ривест Р.Л., Штейн К. – Алгоритмы: построение и анализ: пер. с англ. – 2-е изд. – М.: Издательский дом «Вильямс», 2007. – 1296 с.: ил.

4. Р Газпром 098-2011 Моделирование и оптимизация потоков газа по участкам ГТС для решения задач оперативного диспетчерского управления на основе базы данных ЦПДД ОАО «Газпром».

5. Седжвик Р. Фундаментальные алгоритмы на С +  + . Алгоритмы на графах: пер.с англ. – СПб.: ООО «диаСофтЮП», 2002. – 496 с.

Наиболее актуальной и сложной проблемой, стоящей перед потоковыми комплексами является задача о распределении потоков. При вводе ограничений пропускной способности и управляющих воздействий эта задача по определению [1, 4] становиться задачей управления потоками, включающая в себя сразу несколько типов потоковых задач – транспортные задачи, задачи определения существования потока, задачи о поиске обобщенного потока и пр. В ходе поиска решения одной из таких задач – задачи распределения потоков газа в сложной системе газопроводов с учетом пропускной способности и управляющих воздействий, был разработан новый оригинальный метод решения задачи управления потоками, позволяющий находить решение с учетом условий, возникающих в реально действующих потоковых системах. В статье «Алгоритм управления распределением потоков газа в замкнутой газотранспортной системе»была представлена оригинальная математическая модель и реализующий ее метод расчета оптимального распределения потоков газа в сложной замкнутой системе газопроводов без учета значений ГИС. Также в ней была представлена полученная в ходе разработки метода теорема о решении на реверсивных дугах. В настоящей статье приводится доказательство выдвинутой теоремы и разбирается решение задачи управления распределением потока газа с реверсивными дугами и с учетом значений ГИС.

Основные определения и доказательство теоремы

Напомним постановку задачи для газотранспортной системы без реверсивных дуг. Пусть символ ij обозначает дугу с началом i и концом j. Обозначим через xij переменную величину газового потока в начале дуги ij. По определению для нереверсивной дуги величина xij всегда неотрицательна. Это значит, что газ течёт по дуге из начала i в конец j. Пусть gij есть поступление/распределение на дуге ij. Причём, для величины gij – используем знак « + », если на дуге поступление – приток, и знак «–», если на дуге распределение – отток. Будем считать, что поступление/распределение происходит на середине дуги. Это предположение является важным для описанного метода решения задачи. С учётом сделанных обозначений поток с середины до конца дуги равен xij + gij. Пусть cij – это длина газопровода, который соединяет вершину i с вершиной j. Тогда целевая функция, которая является по сути ТТР, будет иметь следующий вид:

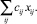(1)

Здесь и в дальнейшем берутся только те индексы i и j, для которых существуют дуги.

В постановку задачи линейного программирования также входит условие баланса в узлах:

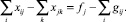(2)

где j номер узла газотранспортной системы; fj – поступление/распределение в узле j (« + » отток, «–» приток)и условие положительности знака потока на дуге в случае отсутствия реверсивных дуг:

xij ≥ 0. (3)

Сформулируем основной результат, доказательство которого будет приведено ниже:

Теорема. Решение, полученное при условии, что разрешается дополнительно хотя бы одна реверсивная дуга, заведомо даёт результат подсчета ТТР не хуже, чем при отсутствии разрешения на реверс этой дуги, либо позволяет решить задачу, у которой не было решения, при изначально заданных условиях.

Замечание: Предполагаем далее, что имеется хотя бы 1 дуга, следовательно, не менее 2 узлов.

Доказательство теоремы разобьём на несколько утверждений и лемму.

Лемма. Пусть имеется две задачи линейного программирования в стандартной форме (см. [2]) у которых различаются только целевые функции. Первая целевая функция имеет вид:

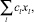(4)

вторая имеет вид:

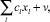(5)

где v есть произвольная действительная константа. Тогда решение 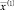первой задачи, на котором достигается min линейной формы (4) является решением второй задачи и на нем целевая функция (5) также достигаем min.

Доказательство. Если 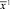оптимальное решение первой задачи, тогда оно удовлетворяет всем условиям и ограничениям и верно равенство:

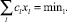(6)

Это значит, что для любого допустимого решения x′ имеем:

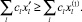(7)

Пусть 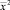есть решение второй задачи, тогда

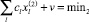(8)

следовательно,

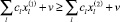
по определению минимума для второй задачи. Отсюда получаем, что

.

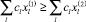С другой стороны из формулы (7) следует, что

.

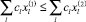Учитывая эти два неравенства, получаем:

.

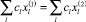Поэтому

.

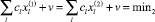Т.е. 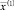является решением второй задачи. Доказательство леммы завершено.

Формула (1) фактически означает, что при подсчёте ТТР поток не меняется при прохождении по дуге. Запишем новую целевую функцию, с учётом того, что дойдя до середины дуги, величина потока меняется.

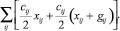(9)

Утверждение 1. При одинаковом векторе ограничений, матрице коэффициентов задачи линейного программирования и фиксированных поступлений/распределений на дугах gij, если найден min линейной формы (1), то на нем линейная форма (9) принимает минимальное значение.

Доказательство. Преобразуем формулу (9)

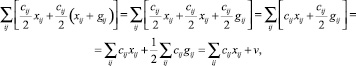(10)

где 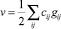– есть константа. Условие Леммы выполняется, что завершает доказательство утверждения 1.

Пусть дуга ij объявлена реверсивной. Добавим (в центре дуги) новую вершину с новым номером k = k(ij). С учетом введенной точки дугу ij заменим на 4 новые дуги ik, kj, ki, jk. Будем считать, что поступление или распределение газа gij на дуге ij переходит в поступление или распределение газа fk в узле k = k(ij), то есть

.

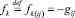Определим новые переменные, которые могут принимать любые действительные значения 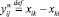и 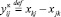. Значение переменной 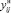– поток на первой половине дуги ij, значение переменной 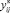– поток на второй половине дуги ij. Учитывая знаки переменных 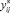, , 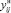получаем 4 варианта потока газа на реверсивной дуге (рис. 1).

Для нереверсивных дуг 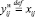и 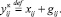. Длины новых 4 дуг положим 1/2 старой:

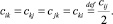
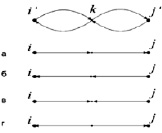
Рис. 1. Возможные направления потоков газа на реверсивной дуге (на рисунке i – началогазопровода, j – конец газопровода):а – поток идет от начала к концу; б – поток идет от конца к началу (реверс); в – встречный поток (реверс на конце); г – разнонаправленный поток (реверс на начале – газопровод становиться донором за счет запаса газа)

Для целевой функции ТТР в случае отрицательных значений на «половинках» дуг формула расчёта включает модули величин, так как ТТР не зависит от направления течения потока:

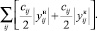(11)

Обозначим через i0j0 реверсивную дугу, тогда учитывая, что xij ≥ 0, xij + gij ≥ 0 и свойство |a – b| ≤ |a + b|, если a, b ≥ 0, имеем оценку:

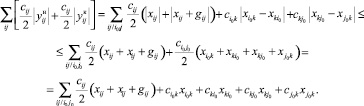(12)

Для дальнейшего рассмотрения будем предполагать, что решение задачи без реверсивных дуг существует. Обозначим его 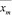, а значение целевой функции на нем через min.

Утверждение 2. Для задачи с объявленной реверсивной дугой i0j0 существует поток 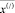, на котором целевая функция задачи с реверсом равна min целевой функции задачи без реверса.

Доказательство. По построению имеем:

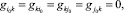(13)

поскольку все поступления и распределения перенесены на центр дуги. На нереверсивных дугах оставим старые значения потока 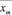. На новых дугах, полученных в результате добавления реверса, зададим следующие значения потока газа:

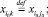
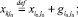
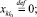
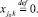(14)

Подставим эти значения в последнее равенство оценки (12):

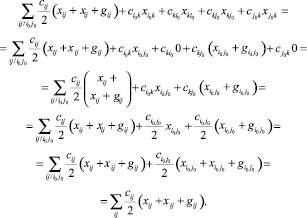(15)

Используя условие (13) можно записать:

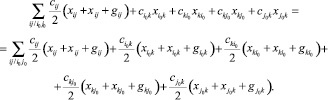(16)

Учитывая (13)–(16) имеем:

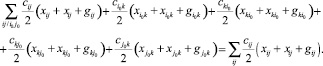(17)

Поэтому в задаче с реверсом есть поток, на котором достигается min задачи без реверса.

Утверждение 3. Для задачи с объявленной реверсивной дугой i0j0 построенный поток 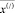, есть допустимое решение новой задачи линейного программирования.

Доказательство. Рассмотрим, как меняется система уравнений баланса в узлах для задачи с добавленной реверсивной дугой.

Появляется новое уравнение условия баланса для узла с номером k:

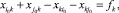(18)

где k = k(i0j0), a 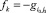(см. рис. 1). Учитывая условия (11) можно записать уравнение (18) в виде:

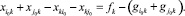(19)

Проверим, что поток с условиями (13)-(14) удовлетворяет уравнению (19). Для этого просто подставим заданные значения в обе части уравнения и получим равенство:

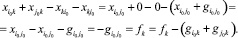(20)

Уравнение условие баланса (2) в узле i0 для нереверсивной дуги i0j0 имеет вид:

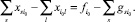(21)

При добавлении признака реверса уравнение (2) в узле i0 приобретает вид:

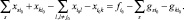(22)

Проверим, что поток с условиями (12)-(13) удовлетворяет уравнению (22). Подставим значения потока в обе части уравнения (22):

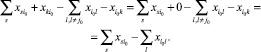(23)

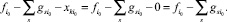(24)

Учитывая равенства (21), (23), (24), получаем, что указанный поток удовлетворяет уравнению (22). Аналогично для конца дуги j0 имеем уравнение баланса вида (2)

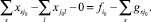(25)

При добавлении признака реверса уравнение (2) в узле j0 приобретает вид:

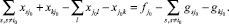(26)

Проверим, что поток с условиями (13)-(14) удовлетворяет уравнению (26). Действуя аналогично, получаем:

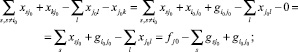(27)

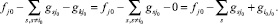(28)

Учитывая равенства (25), (27), (28), получаем, что указанный поток удовлетворяет уравнению (26). Остальные условия (уравнения) выполняются автоматически, так как по построению данного решения оно удовлетворяет тем уравнениям, которые не менялись.

Объединив вместе Утверждения 2 и 3, получаем.

Утверждение 4. Для задачи с объявленной реверсивной дугой i0j0, построенный поток 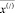есть допустимое решение новой задачи. Значение новой целевой функции на нем совпадает с min целевой функции задачи без реверса.

Обозначим новую целевую функцию для задачи с реверсивной дугой:

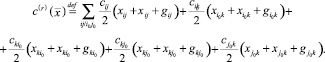(29)

Оптимальное решение 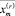задачи с реверсом, очевидно, удовлетворяет условию:

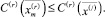(30)

Утверждение 5. Для любого решения 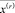задачи с реверсом дуги i0j0 верно, что решение в новых переменных 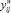и 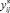является допустимым решением задачи, где поток на дуге i0j0 разделён на два с одним из направлений как на рис. 1 (а-г).

Доказательство. Проверим, что это верно для всех вершин, кроме i0 и j0. Для этого уравнения вида (2) преобразуем следующим образом:

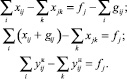(31)

Проверим согласование потока в середине дуги i0j0. Это следует из преобразования равенства (18)

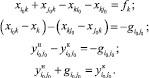(32)

Проверим согласование потока в вершине i0. Для этого преобразуем уравнение (20)

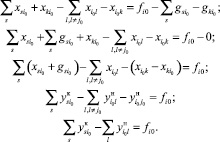(33)

Осталось проверить согласование потока в вершине j0. Аналогичным образом преобразуем уравнение (26)

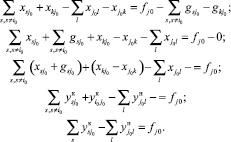(34)

Равенства (31)–(34) показывают, что поток, выраженный в новых переменных 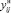и 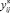, удовлетворяет всем требуемым условиям.

Доказательство Теоремы. Рассмотрим Случай 1, когда решение задачи (1–3) без реверсивных дуг существует, обозначим это решение символом 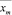, а значение целевой функции на этом решении через MIN. Пусть дуге i0j0 присвоен признак реверса. Согласно Утверждению 4 существует поток 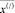– допустимое решение задачи с реверсом. Значение новой целевой функции на этом потоке совпадает с MIN целевой функции задачи без реверса:

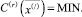
У задачи с реверсом есть оптимальное решение 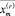, для которого выполнено неравенство (30) 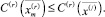Следовательно, получаем:

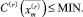(35)

Для задачи с реверсом в новых переменных 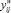, 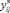в целевую функцию (11) входят модули величин потоков:

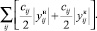
Комбинируя вместе неравенство (12), (16), (29), получаем, что:

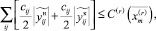(36)

где величины 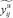, 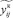вычислены по решению 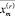. Из неравенств (36) и (37) так же очевидно следует, что:

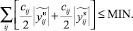(37)

То есть новое решение не хуже решения без реверса. Кроме того, согласно Утверждению 5 решение 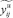, 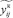является допустимым решением задачи, где поток на дуге i0j0 разделён на два. Таким образом, все ограничения соблюдены, и Теорема 1 доказана для первого случая при добавлении реверса на 1 дугу. Случай 2, когда изначальная задача не имела решения, а после добавления реверса на дугу решение появилось, показан на рис. 2, где приведен один из возможных вариантов данного случая.

Если по условию задачи признак реверса получают несколько дуг, то проводя аналогичные рассуждения можно доказать все утверждения, где в формулировке будут несколько дуг с реверсом. Если дуги с реверсом не имеют общих вершин, то добавляются новые уравнения и доказательства проводятся по той же схеме.

Рис. 2. Пример решение задачи с введением условия реверса дуги:а – дуга не реверсивная – решения нет; б – введение реверса дуги дает решение задачи

Пусть также есть реверсивные дуги i0v0 и v0t0 с общей вершиной v0. Обозначим через k1 = k1(v0t0) середину дуги i0v0 и через k2 = k2(v0t0) середину дуги v0t0. Покажем для этого случая схему доказательства на примере Утверждения 5. Уравнение баланса (2) в узле v0 для случая без реверса

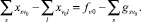(38)

При добавлении признаков реверса уравнение (2) в узле v0 приобретает вид:

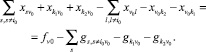(39)

Проверим согласование потока в узле v0, преобразуя равенство (39)

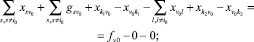
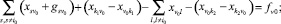(40)

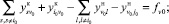
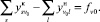
Теорема доказана.

Осталось заметить, что если в узле сходятся несколько (больше 2) реверсивных дуг, то записывая условие баланса в этом узле и аналогично группируя члены уравнений или неравенств, получаем требуемые утверждения во всех возможных случаях.

Описание метода подключения ГИС для газотранспортной системы

Рассмотрим, для начала, газотранспортную систему без реверсивных дуг. Пусть на некоторых дугах имеются газо-измерительные станции – ГИС. В результате проведения замеров на дугах могут быть либо точные данные потока газа, либо значение в диапазоне. Задача: найти оптимальное по заданному критерию распределение газа с учетом новых условий замеров на ГИС. Определим вектор {gmsTij}, который для некоторых дуг, где есть ГИС, равен 1, а остальные координаты равны 0. Идея решения в том, что ставятся ограничения на значения переменных, которые моделируют поток. Рассмотрим два случая.

Случай A. Значение потока на дуге имеет постоянное (не отрицательное) значение, обозначается gmsij. В виде формул это можно записать так:

xij = + gmsij. (41)

Используя описанное выше соответствие индексов T, имеем

T: gmsij = gmsT(ij) → gmsl;

T: gmsTij = gmsTT(ij) → gmsTl. (42)

Поэтому условие на ГИС можно задать так:

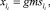(43)

где li есть некоторое подмножество множества номеров дуг.

Пусть число дуг с ГИС равно Z. Тогда i = 1, 2, ..., Z. И вектор длины n:

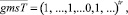(44)

где единицы стоят на местах с номерами li, и n – число дуг.

Равенства для нашего метода следует заменить на два неравенства:

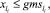
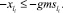(45)

По условию задачи ГИС могут быть в начале или в конце дуги. Вектор GIEl обозначает, где находится ГИС: в начале дуги – координата равна 0 или в конце дуги – координата равна 1. Математически это можно записать так:

1) ГИС в начале дуги: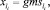

2) ГИС в конце дуги: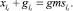

Тогда

1)

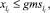
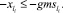
2)

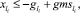
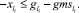
В матричном виде:

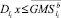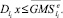или (46)

где 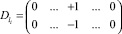– матрица размера 2×n и li столбец не нулевой,

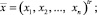
или

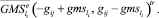
Обозначим через Dgms матрицу размера (2∙Z)×n вида

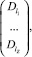
а через 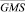– обозначим вектор

,

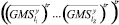где y ∈ {b, e}.

Случай B. Значение (положительное) потока на дуге задаётся значением и диапазоном, обозначается Devij . В виде формул это можно записать так:

0 ≤ + gmsij – Devij∙gmsij ≤ xij ≤ + gmsij + Devij∙gmsij. (47)

В этом случае задано, что 0 ≤ Devij ≤ 1.

Используя описанное выше соответствие индексов T, имеем

T: Devij = DevTij → Devl. (48)

Поэтому условие на ГИС можно задать следующим образом:

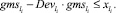
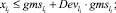(49)

Для нашего метода неравенства:

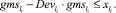
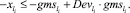(50)

3) ГИС в начале дуги:

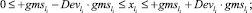
4) ГИС в конце дуги:

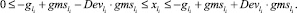
Тогда

3)

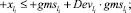
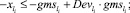
4)

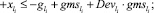
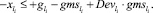
В матричном виде получаем:

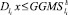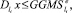или (51)

где

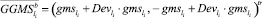
или

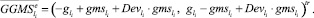
Обозначим через Dggms матрицу размера (2∙Z)×n вида:

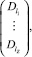
а через 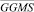– обозначим вектор

,

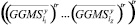где y ∈ {b, e}.

Теперь можно поставить задачу линейного программирования, которая учитывает метрические характеристики потока, задавая матрицу

,

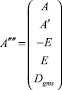вектор

и вектор линейной формы .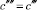

Перейдем к рассмотрению случая с реверсивными дугами. Нам придётся учитывать знак потока дуги. Знак « + » означает, что поток течёт из начала в конец, знак «–» поток течёт из конца в начало. Также будем учитывать ГИС в начале или конце. Суть метода – поставить ограничения на новые дуги, чтобы потоки на дуге с реверсом совпадали с потоком на новых дугах, то есть моделируется поток на реверсивной дуге.

Случай A. Знак потока « + ». Поток совпадает с начальным направлением. Пусть l принимает значения номеров всех дуг.

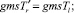
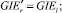
Если дуга в старой нумерации не реверсивная, тогда используя «старую» матрицу шифратор найдем двойной номер ij = ij(l) и в «новой» матрице смежности в ячейке с номером ij берём значение r. После этого присваиваем 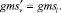В итоге перебираем n – M «старых» дуг, и n – M новых дуг.

Если дуга в старой нумерации суть реверсивная, тогда используя двойной номер ij = ij(l) по матрице «биекции» находим номер k = k(ij) фиктивной вершины.

Случай A. 1. ГИС в начале дуги.

В «новой» матрице смежности из ячеек с номерами ik, kj, jk, ki берём последовательно значения и присваиваем

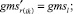
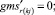
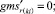
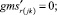
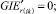
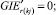
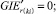
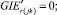
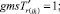
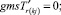
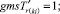
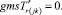(52)

Случай A 2. ГИС в конце дуги.

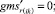
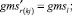
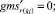
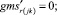
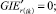
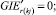
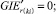
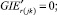
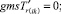
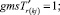
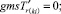
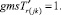(53)

Случай AA. Знак потока может быть и « + » и «» на реверсивных дугах. Знак потока « + ». Совпадает с начальным направлением. Знак потока «». Поток течёт в противоположную сторону от начального направления. (Если знак « + » этот случай описан выше.)

Случай AA. 1. ГИС в начале дуги. Знак потока «» на реверсивной дуге.

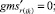
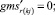
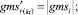
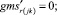
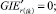
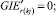
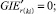
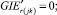
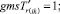
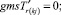
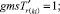
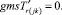(54)

Случай AA. 2. ГИС в конце дуги. Знак потока «» на реверсивной дуге.

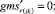
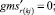
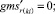
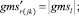
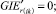
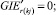
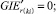
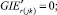
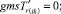
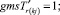
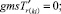
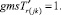(55)

Случай B. Знак потока « + ». Поток совпадает с начальным направлением. Значение ГИС может учитываться в диапазоне.

Случай B. 1. ГИС в начале дуги. Нижняя граница диапазона больше 0.

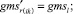
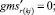
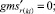
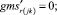
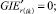
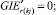
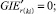
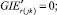
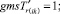
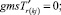
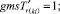
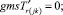
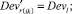
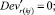
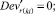
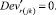(56)

Случай B 2. ГИС в конце дуги. Нижняя граница диапазона больше 0.

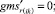
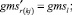
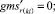
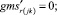
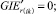
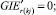
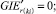
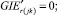
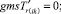
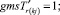
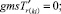
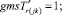
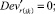
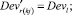
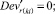
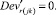(57)

Случай BB. Знак потока может быть и « + » и «» на реверсивных дугах.

Знак потока « + ». Поток совпадает с начальным направлением. Знак потока «». Поток течёт в другую сторону от начального направления. Если знак « + » этот случай описан выше.

Случай BB 1. ГИС в начале дуги. Знак потока «» на реверсивной дуге. Нижняя граница диапазона больше 0 по модулю.

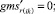
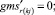
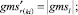
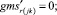
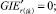
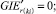
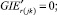
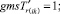
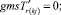
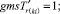
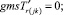
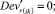
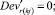
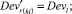
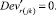(58)

Случай BB 2. ГИС в конце дуги. Знак потока «» на реверсивной дуге. Нижняя граница диапазона больше 0 по модулю.

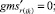
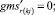
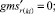
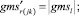
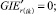
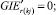
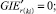
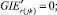
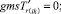
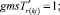
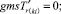
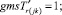
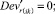
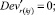
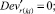
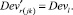(59)

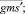
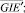
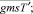
В результате, заданы все n + 3∙M∙(n + M) значений для векторов 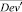и задача сведена к предыдущему случаю, где нет реверса.

Постановка задачи линейного программирования для решения симплекс методом завершена.

Заключение

Метод, изложенный в данной работе, позволяет производить постановку разных потоковых задач в зависимости от топологии рассматриваемой газотранспортной системы и граничных условий. В статье обоснована возможность постановки задачи для решения симплекс методом [2, 3] с добавлением признака дуги и с учетом замеров реально проходящего газа через газопроводы. Разработанный метод многовариантен и позволяет оперативно решать наиболее актуальные задачи потоковых комплексов.

Выражаем благодарность В.М. Простокишину за внимание к работе и конструктивное обсуждение.

Библиографическая ссылка