Генераторы К(5/3) типа дерево и К(3/31/2) типа снежинка используются для аппроксимации гладкой конфигурации границ плоских объектов квазифрактальными кривыми с фрактальной размерностью 1,465 без существенного изменения площади их поверхности или для аппроксимации случайной траектории развития определенных ветвящихся процессов из однотипных или разнотипных центров-источников с фрактальными размерностями, близкими к мерности топологического пространства [1, 2]. Анализ вероятных конфигураций квазифрактальных межфазных границ проводили в соответствии с общими положениями опубликованных ранее в [3-7] методик комбинаторного и итерационного модулярного дизайна различных детерминированных фрактальных структур в 2 пространстве.
Методом i-кратной итерации генераторов гомологического ряда
К((3n + 1)/(2n + 1))
типа дерево (рис. 1, а) на периметрах ячеек сеток Кеплера (как наиболее простых аппроксимантов набора сечений микрочастиц фаз на поверхности покрытий) возможно получение извилистых конфигураций межфазных границ квазифрактального характера. С каждой i-й итерацией средняя длина межфазных границ увеличивается в соответствии с соотношением
Li = (3n + 1)Li-1/(2n + 1).
Каждая i-я итерация генераторов гомологического ряда K((n + 1)/x) типа снежинка (рис. 1, б) на узлах сеток Кеплера приводит к его расщеплению на (n + 1) линейных отрезков-границ с общей длиной (n + 1)x/i, которая равна стороне полигона с учетом порядкового номера итерации. Величина коэффициента затухания роста снежинок х меньше 1 и учитывается при расчете скорости изменения общей длины квазифрактальной линии, т.е.
Li = [(n + 1)/х]Li-1.
С увеличением размеров полигонов-ячеек сеток Кеплера вклад фрактализации с помощью генераторов типа дерево в общую длину межфазных границ закономерно снижается (рис. 2, а).
В случае использования генераторов типа снежинка этот вклад регулируется с помощью учета коэффициента затухания их роста на узлах сеток Кеплера, для каждой из которых, даже для гетерополигонных сеток, известна поверхностная концентрация этих узлов (рис. 2, б). Очевидно, что для узлов, в которых сходятся разнотипные полигоны (например, в таких сетках Кеплера как 34334, 3636, 488 и других), используются гибридные генераторы снежинок соответствующего состава.
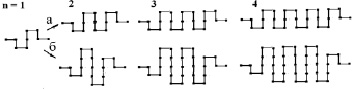
Рис. 1. Первые пять генераторов гомологического ряда К((3n + 1)/(2n + 1)) типа дерево (а) и гомологического ряда K((n + 1)/x) типа снежинка (б)
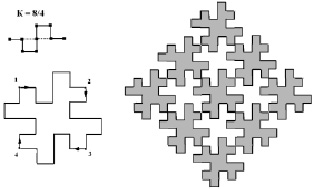
Рис. 2. Предфрактальные кривые 3-го поколения, полученные итерацией дерева К(4/3)на периметрах тригонных (1), тетрагонных (2) и гексагонных (3) ячеек сеток Кеплера (а). Предфракталы 3-го поколения, полученные двукратной итерацией снежинок К(3/х) на узлах сетки 333333 (1), итерацией снежинок К(4/х) на узлах сетки 4444 (2) и снежинок К(6/х) на узлах сетки 666 (3)
Полученные результаты анализа вероятных квазифрактальных конфигураций межфазных границ могут быть использованы, в частности, при оценке вклада их относительной площади на поверхности композиционных материалов и покрытий в эффект синергизма антифрикционных свойств функциональных компонентов композита при трении и износе в соответствии с синергической моделью «концентрационной волны» [8, 9]. В качестве аппроксимантов для гладких конфигураций межфазных границ и источников роста снежинок могут быть использованы плоские сетки Кеплера и Кеплера-Шубникова, а также соответствующие им системы упорядоченных узлов.
Библиографическая ссылка
Иванов В.В., Таланов В.М. ИТЕРАЦИОННОЕ МОДЕЛИРОВАНИЕ КОНФИГУРАЦИЙ КВАЗИФРАКТАЛЬНЫХ МЕЖФАЗНЫХ ГРАНИЦ С ПОМОЩЬЮ ГЕНЕРАТОРОВ ТИПА ДЕРЕВО И СНЕЖИНКА НА 2D-СЕТКАХ // Современные наукоемкие технологии. 2012. № 11. С. 22-23;URL: https://top-technologies.ru/ru/article/view?id=31095 (дата обращения: 23.12.2025).



