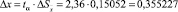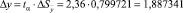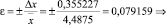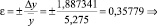Необходимость производства в точности измерений требуют правильного подхода к его оценке на современном уровне теории погрешностей. Наиболее точно определить величину абсолютной и относительной погрешности, с определенной надежностью, позволяет распределение Стьюдента. Например: «После проверки двух партий колец подвергшиеся шлифованию получены следующие результаты фактического отклонения действительного размера диаметра кольца от номинального:
xi (мкм): 3,9; 4,1; 4,2; 4,4; 4,5; 4,7; 5,0; 5,1;
yi (мкм): 2,4; 2,8; 4,1; 4,4; 5,6; 6,8; 7,2; 8,9.
Для оценки точности измерения необходимо вычислить абсолютную и относительную погрешности, степень надежности α = 0,95».
|
Вычисления для партии 1 |
Вычисления для партии 2 |
|
Среднеквадратичную погрешность результата измерений: |
|
|
|
|
|
Значение коэффициента Стьюдента tα для надежности α = 0,95: tα = 2,36. |
|
|
Абсолютная погрешность: |
|
|
|
|
|
Относительная погрешность: |
|
|
погрешность измерений составляет ≈ 8 % |
погрешность измерений составляет ≈ 36 % |
Полученные результаты позволяют сделать вывод о том, что вторая партия колец подшипников подвергшиеся шлифованию на 36 % состоит из брака. Следовательно, необходимо выявить и устранить причины возникновения погрешностей.
Библиографическая ссылка
Ребро И.В., Мустафина Д.А. Расчет погрешностей при контроле наружнего диаметра кольца подшипников после операции шлифования // Современные наукоемкие технологии. 2012. № 10. С. 51-52;URL: https://top-technologies.ru/ru/article/view?id=30994 (дата обращения: 05.03.2026).




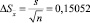 , где s = 0,425735
, где s = 0,425735
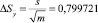 , где s = 2,261952
, где s = 2,261952