Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое число. Поток на графе – это некоторая функция, заданная на дугах графа. В нашем случае поток на графе задается в виде функции плотности распределения интервалов по времени между требованиями.
Назовем сетевые потоки неконфликтными, если на данном участке сети они не пересекаются, и конфликтными – в противном случае. Вершинами графа будем считать узловые точки – точки, в которых либо расположены источники или потребители информации, либо происходит пересечение конфликтных потоков. То есть узловые точки образуются пересечением многоканальных магистралей. Будем считать распределение интервалов по времени в каждом из потоков требований (каналов) подчиненным распределению Эрланга:
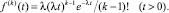
Этот закон позволяет описывать потоки достаточно высокой плотности. В частности, для транспортных потоков гипотеза о распределении интервалов по времени между подряд идущими автомобилями по закону Эрланга подтверждается при интенсивности движения по каждой полосе до 500 авт./ч .
Пусть {lj} – множество дуг графа, {zj} – множество вершин (узловых точек). Дуга представляет собой часть многоканальной магистрали, заключенную между двумя вершинами (узловыми точками). Присвоим магистралям сети идентификационные номера WAY_i, i ∈ N. В этом случае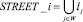 
. Тогда можно представить граф с помощью следующих связанных матриц:
I.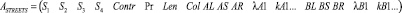 
1) № – номер строки матрицы соответствует номеру дуги графа, соединяющей узловые точки I и II; количество строк соответствует количеству дуг графа;
2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;
3) S3 и S4 – пересекающиеся магистрали, образующие вершину II графа;
4) Contr – тип узловой точки;
5) Pr – наличие приоритета (главная или второстепенная магистраль);
6) Len – длина дуги между узловыми точками;
7) Col – количество потоков на дуге;
8) AL – допустимость поворота налево из направления А в вершине II;
9) AS – допустимость движения прямо из направления А вершине II;
10) AR – допустимость поворота направо из направления А вершине II;
11) λА1, λА2 и т.д. – параметр λ в направлении А;
12) kA1, kA2 и т.д. – параметр k в направлении А;
13) BL – допустимость поворота налево из направления В вершине I;
14) BS – допустимость движения прямо из направления В вершине I;
15) BR – допустимость поворота налево из направления В вершине I;
16) λВ1, λВ2 и т.д. – параметр λ в направлении В.
17) kB1, kB2 и т.д. – параметр k в направлении В.
II.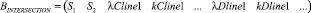 
1) № строки совпадает с номером дуги графа, соединяющей узловые точки I и II в матрице ASTREETS;
2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;
3) λCline1, λCline2 и т.д. –параметр λ потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;
4) kC line1, kC line2 и т.д. –параметр k потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;
5) λD line1, λD line2 и т.д. – параметр λ потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I;
6) kD line1, kD line2 и т.д. – параметр k потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I.
Рассмотрим следующую задачу: определить оптимальное (из множества
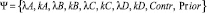
известных способов) распределение потоков для данной вершины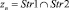 
.
Критерием оптимизации, в зависимости от преследуемой цели, может служить:
1) 
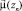– вес вершины zn (узловой точки) для потока данного направления;
2) 
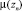– вес вершины zn (узловой точки);
3) 
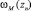– средняя задержка требования выбранных направлений.
Рассмотрим узловую точку (УТ), в которой происходит пересечение конфликтных потоков. Одна часть потоков (назовем их главными) проходит через УТ беспрепятственно. Требования второй части потоков (второстепенных) ожидают возникновения достаточных интервалов по времени между требованиями главных потоков для пересечения УТ. Назовем такую УТ узловой точкой I типа.
Для узловой точки I типа:
1) 
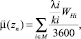
где М – множество выбранных направлений;
2) 
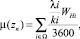
где W – множество всех направлений;
3) 
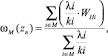
где М – множество выбранных направлений.
Здесь принято обозначение: WН – средняя задержка (в секундах) в УТ одного требования второстепенного направления в потоке с параметрами распределения λ и k/
Рассмотрим теперь узловую точку (УТ) другого вида, в которой также происходит пересечение конфликтных потоков. Для возможности пересечения УТ поочередно перекрывается движение для одной из групп неконфликтных потоков на фиксированное время Ti. Назовем такую УТ узловой точкой второго типа. Для узловой точки II типа:
1) 
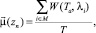
где М – множество выбранных направлений, a ∈ {1; 2};
2) 
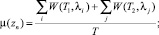
3) 
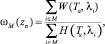
где М – множество выбранных направлений, a ∈ {1; 2}.
Здесь приняты обозначения:
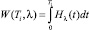(треб.∙с.) – суммарная задержка всех требований данного потока за один цикл регулирования T = T1 + T2; H(t) – число требований, прибывающих к данной точке дороги за интервал времени (0; t).
Оптимальное распределение потоков в узловой точке является решением задачи (в зависимости от преследуемой цели):
1) 
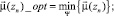
2) 
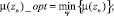
3) 
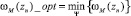
Вся необходимая для решения задачи информация о входящих потоках содержится в матрицах ASTREETS и BINTERSECTION .
Лемма 1.
Пусть задана вершина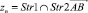 
(с точностью до порядка Str1 и Str2). Параметры распределения Эрланга входящих в вершину 
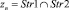потоков заданы:
1) в матрице ASTREETS в строке
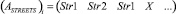
– направление В;
2) в матрице BINTERSECTION в строке (BINTERSECTION)i в направлениях С и D;
3) в матрице ASTREETS в строке
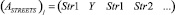
– в направлении А.
Вышеизложенное представление распределения потоков по сети и, в частности, в узловых точках, может быть использовано для определения оптимальной схемы организации движения автотранспортных средств по улично-дорожной сети.
Библиографическая ссылка
Наумова Н.А. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ПОТОКОВ В УЗЛОВОЙ ТОЧКЕ // Современные наукоемкие технологии. – 2012. – № 10. – С. 50-51;URL: https://top-technologies.ru/ru/article/view?id=30993 (дата обращения: 23.11.2024).