В процессе работы над доказательством правильности гипотезы Римана придерживались сильной теоремы Гёделя о неполноте: «Логическая полнота (или неполнота) любой системы аксиом не может быть доказана в рамках этой системы. Для ее доказательства или опровержения требуются дополнительные аксиомы (усиление системы)».
Неполнота известного закона распределения простых чисел состоит в следующем:
1) в порядке n = 1, 2, 3, ...не учитывается нуль (усеченный натуральный ряд чисел);
2) традиционный ряд простых чисел a(n) = 2, 3, 5, 7, ... не учитывает нуль и единицу;
3) допущение о том, что «отношение x к π(x) при переходе от данной степени десяти к последующей всё время увеличивается примерно на 2,3» является явно некорректным;
4) утверждение, что 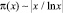 , предложенное в 1896 году Гауссом, переводит простые числа из десятичной системы счисления в систему счисления с основанием e = 2,71828...;
, предложенное в 1896 году Гауссом, переводит простые числа из десятичной системы счисления в систему счисления с основанием e = 2,71828...;
5) мощность простых чисел π(x) в ряду натуральных чисел по порядкам приняты в десятичной арифметике, а отношение x/ln x – в системе счисления натуральных логарифмов.
Придерживаясь идей математиков Пойа и Адамара о математических изобретениях, мы решили выйти за пределы современных достижений закона Гаусса о простых числах и преобразований Римана в комплексных числах, понимая, что при равномощности простых чисел натуральным числам достаточно будет математических преобразований в вещественных числах.
Полный ряд, методика и данные. Простое число́ – это натуральное число N = {0, 1, 2, 3, 4, 5, 6, ...} с натуральным делителем 1 (деление на самого себя – избыточно).
От простых чисел P = {0, 1, 2, 3, 5, 7, ...} «лестницы Гаусса-Римана» отделили «ступеньки» с параметром прирост простых чисел pj = Pj+1 – Pj, где j = 0, 1, 2, 3, 4, ... – порядок-ранг. Отказ от системы счисления с основанием e = 2,71828... привел к переводу в двоичную систему. Поняли, что математики, увлекшись факторизацией простых чисел, забыли о пользе разложения чисел.
В табл. 1 показано преобразование 500 простых чисел из десятичной системы в двоичную. Разложение простых чисел происходит по известным простым правилам по разрядам-рангам i = 0, 2, 3, 4, ... Затем по двоичным (вещественным) числам z были выявлены отличительные особенности распределения простых чисел и их приростов по критичной линии Римана и огибающим левую границу 1 линиям. Факторный анализ P = {0, 1, 2, 3, 5, 7, ..., 3559} дал число 1/2.
Таблица 1
Параметры полного ряда 500 простых чисел в двоичной системе счисления
|
Параметры |
Простое число в двоичной системе |
Прирост в двоичной системе |
||||||||||||||||||||||||
|
Порядок-ранг j |
Простое число P |
Прирост p |
Огибающая |
Разряд-ранг числа |
Огибающая |
Разряд-ранг |
||||||||||||||||||||
|
граница |
разряд |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
граница |
разряд |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|||
|
Часть простого числа |
2–1 |
Часть прироста |
2-1 |
|||||||||||||||||||||||
|
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
32 |
16 |
8 |
4 |
2 |
1 |
|||||||||
|
0 |
0 |
1 |
1 |
1 |
1 |
½ |
1 |
1 |
1 |
½ |
||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
Тривиальные нули |
1 |
½ |
1 |
1 |
Тривиальные нули |
1 |
½ |
||||||||||||||
|
2 |
2 |
1 |
2 |
2 |
1 |
0 |
½ |
1 |
1 |
1 |
½ |
|||||||||||||||
|
3 |
3 |
2 |
2 |
2 |
1 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||||||||||||
|
4 |
5 |
2 |
4 |
3 |
1 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
|||||||||||||
|
5 |
7 |
4 |
4 |
3 |
1 |
1 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
||||||||||||
|
6 |
11 |
2 |
8 |
4 |
1 |
0 |
1 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||||||||||
|
7 |
13 |
4 |
8 |
4 |
1 |
1 |
0 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
|||||||||||
|
8 |
17 |
2 |
16 |
5 |
1 |
0 |
0 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
|||||||||||
|
9 |
19 |
4 |
16 |
5 |
1 |
0 |
0 |
1 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
||||||||||
|
10 |
23 |
6 |
16 |
5 |
1 |
0 |
1 |
1 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
||||||||||
|
11 |
29 |
2 |
16 |
5 |
1 |
1 |
1 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
|||||||||||
|
12 |
31 |
6 |
16 |
5 |
1 |
1 |
1 |
1 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
||||||||||
|
13 |
37 |
4 |
32 |
6 |
1 |
0 |
0 |
1 |
0 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
|||||||||
|
14 |
41 |
2 |
32 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||||||||
|
15 |
43 |
4 |
32 |
6 |
1 |
0 |
1 |
0 |
1 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
|||||||||
|
16 |
47 |
6 |
32 |
6 |
1 |
0 |
1 |
1 |
1 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
|||||||||
|
17 |
53 |
6 |
32 |
6 |
1 |
1 |
0 |
1 |
0 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
|||||||||
|
18 |
59 |
2 |
32 |
6 |
1 |
1 |
1 |
0 |
1 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||||||||
|
19 |
61 |
6 |
32 |
6 |
1 |
1 |
1 |
1 |
0 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
|||||||||
|
20 |
67 |
4 |
64 |
7 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
||||||||
|
32 |
127 |
4 |
64 |
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
½ |
4 |
3 |
1 |
0 |
0 |
½ |
||||||||
|
33 |
131 |
6 |
128 |
8 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
|||||||
|
55 |
251 |
6 |
128 |
8 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
|||||||
|
56 |
257 |
6 |
256 |
9 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
½ |
4 |
3 |
1 |
1 |
0 |
½ |
||||||
|
98 |
509 |
12 |
256 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
½ |
8 |
4 |
1 |
1 |
0 |
0 |
½ |
|||||
|
99 |
521 |
2 |
512 |
10 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||||
|
173 |
1021 |
10 |
512 |
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
½ |
8 |
4 |
1 |
0 |
1 |
0 |
½ |
||||
|
174 |
1031 |
2 |
1024 |
11 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
|||||
|
310 |
2039 |
14 |
1024 |
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
½ |
8 |
4 |
1 |
1 |
1 |
0 |
½ |
|||
|
311 |
2053 |
10 |
2048 |
12 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
½ |
8 |
4 |
1 |
0 |
1 |
0 |
½ |
||
|
499 |
3557 |
2 |
2048 |
12 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
½ |
2 |
2 |
1 |
0 |
½ |
||||
|
500 |
3559 |
12 |
2048 |
12 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
½ |
8 |
4 |
1 |
1 |
0 |
0 |
½ |
||
Примечание. Разрывами таблицы показаны начало и конец блоков из 0 и 1 в ряде из 500 простых чисел.
В табл. 1 показаны симметричные геометрические узоры, однако из анализ мы не проводили. Видно, что любое простое число перед собой имеет отношение 1/2. Но оно в сумму слагаемых не входит. Комплекс математических выражений параметров ряда имеет вид:
ij = (1, m); j = (0, n); m = 6, n = 6; (1)
Pj+1 = Pj + pj; pj = Pj+1 – Pj ; (2)
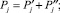
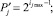
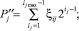
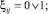 (3)
(3)
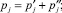
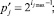
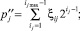
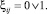 (4)
(4)
В табл. 1 имеем два типа нулей – тривиальные (пустые клетки) и нетривиальные (0). Первые для простых чисел расположены слева от ломаной линии 1. А нетривиальные нули располагаются внутри двух столбцов с 1. Сложнее с приростом – огибающая всех 1 является волновой, а сама линия всегда касается критической линии 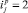 .
.
Математический «ландшафт». В фильмах «De Code» (19.07; 26.07 и 02.08.2011) показывали трехмерную картину дзета-функции Римана. Все обращают внимание на нетривиальные нули на критической линии. Их уже насчитали несколько триллионов.
Расклад в двоичной системе бесконечно высокие «горы» превращает в выступы одинаковой высоты, равной единице. На рис. 1 приведен ландшафт из 24 первых простых чисел.
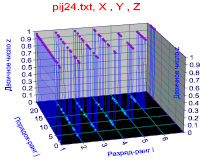
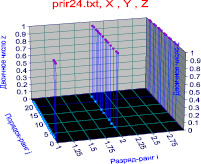
Простые числа в начале ряда распределения; Прирост простых чисел в начале ряда распределения
Рис. 1. Математический «ландшафт» двоичного распределения 24 первых простых чисел
На рис. 1 появляется «потолок» из 1, кроме «пола» из нетривиальных нулей. Между ними существует неизвестная факторная связь. Тогда сложная поверхность дзета-функция Римана, из-за представления в комплексных числах, преобразуется в «двухслойный пирог».
Реперы. Они имеются по левым верхним углам блоков простых чисел. Именно при переходе к ним происходит скачок прироста простого числа. Поэтому мощностью ряда простых чисел вполне можно управлять с помощью реперов, они будут надежнее десятичных разрядов.
Из табл. 1 выпишем узловые значения NR (табл. 2) и другие параметры реперов.
Таблица 2
Асимптотические реперы ряда из 500 простых чисел
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
j |
0 |
2 |
4 |
6 |
8 |
13 |
20 |
33 |
56 |
99 |
174 |
311 |
|
Pij |
0 |
2 |
5 |
11 |
17 |
37 |
67 |
131 |
257 |
521 |
1031 |
2053 |
|
NR |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
|
Pij – NR |
-1 |
0 |
1 |
3 |
1 |
5 |
3 |
3 |
1 |
9 |
7 |
5 |
Измерение мощности ряда простых чисел по реперам гораздо экономичнее π(x).
Влияние простых чисел по разрядам. Из табл. 1 видно, при i = 0 есть z0 = 1/2.
А в столбце i = 1 (рис. 2) имеется всего один нетривиальный нуль на протяжении j = (0, n), т.е. до j = (0, ∞). По неявно данному нами закону Гаусса «нормального» распределения имеем
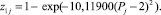 (5)
(5)
Тогда простое число 2 является критичным, а некритичный ряд начинается с 3.
На критичной линии есть формула
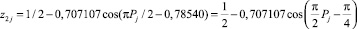 (6)
(6)
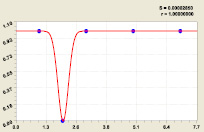
Рис. 2. График формулы (5) распределения двоичного числа: S – дисперсия; r – коэффициент корреляции
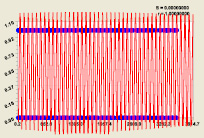
Рис. 3. График формулы (6) распределения двоичного числа
Выполнено (рис. 3) доказательство «знаменитой гипотезы Римана о том, что вещественная часть корня всегда в точности равна 1/2». Частота колебания равна π/2, а сдвиг – π/4.
Появились две фундаментальные физические постоянные: в формуле (5) – число Непера e = 2,71828... (число времени); в выражении (6) – число Архимеда π = 3,14159...(число пространства). Что означает 0,707107 – мы пока не знаем.
Затем получена (рис. 4) модель
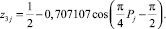 (7)
(7)
Монтгомери и Дайсон применили статистические физические методы анализа распределений применительно к ряду простых чисел и определили среднюю частоту появлений нулей.
Но, оказывается, эта средняя частота через двоичное преобразование простых чисел получается функционально связанным с числом пространства π = 3,14159... .
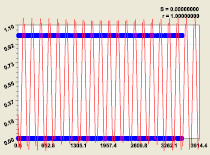
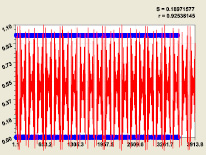
Статистическая модель (7) при третьем разряде; Статистическая модель (8) при четвертом разряде
Рис. 4. Графики распределения двоичного числа составляющих простых чисел
С остатками до 0,25 для четвертого разряда была получена (рис. 4) модель
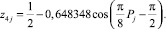 (8)
(8)
Для пятого и шестого разрядов (рис. 5) были получены закономерности:
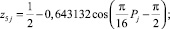 (9)
(9)
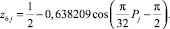 (10)
(10)
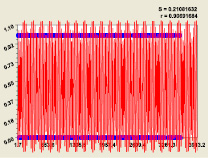
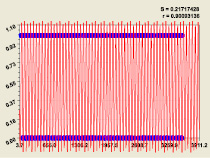
Статистическая модель (9) при пятом разряде; Статистическая модель (10) при шестом разряде
Рис. 5. Графики распределения двоичного числа составляющих простых чисел
Заметно, что с увеличением разряда двоичной системы счисления остатки (абсолютная погрешность) возрастает. Это видно на графиках по снижению коэффициента корреляции.
В 1972 г. Монтгомери доказал характер расположения нулей на критичной линии. Из формул (6) и других видно, что они (а также и 1) действительно колеблются. Мы объясняем стремление простых чисел, а также их преобразованных в двоичной системе счисления 0 и 1, разбегаться друг от друга из-за силы, возникающей в прогрессии 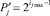 . А нетривиальные нули разбегаются в плоскости (i, j) по закономерности (3) для слагаемой
. А нетривиальные нули разбегаются в плоскости (i, j) по закономерности (3) для слагаемой 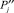 при
при 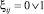 .
.
Для седьмого и восьмого разрядов (рис. 6) получены формулы аналогичной конструкции:
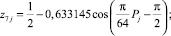 (11)
(11)
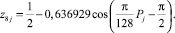 (12)
(12)
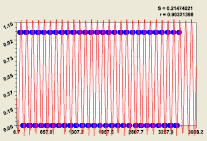
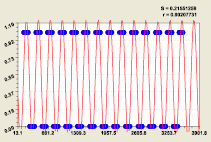
Статистическая модель (11) при седьмом разряде; Статистическая модель (12) при восьмом разряде
Рис. 6. Графики распределения двоичного числа составляющих простых чисел
Для девятого и десятого разрядов (рис. 7) были получены аналогичные закономерности:
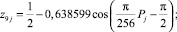 (13)
(13)
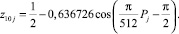 (14)
(14)
Для 11-го разряда (рис. 8) аналогично была получена (при этом z12j = 1) формула
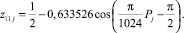 (15)
(15)
Существует среди математиков утверждение: в распределении простых чисел нет никакой геометрии. Узоры на двоичной матрице в табл. 1 и по остаткам на рис. 8 опровергают это утверждение. Однако, чем и как их идентифицировать, мы пока не знаем.
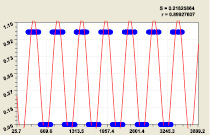
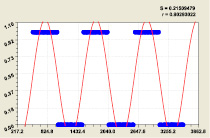
Рис. 7. Графики распределения двоичного числа составляющих простых чисел
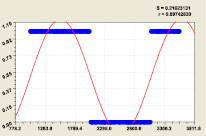
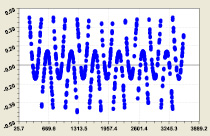
Статистическая модель (15) при 11-м разряде; Остатки после формулы (13) девятого разряда
Рис. 8. Графики распределения двоичного числа составляющих простых чисел
Влияние прироста по разрядам. Бернхард Риман в 1859 году по результатам анализа дзета-функции утверждал, что нули находятся на одной линии. Ныне полагают, что она как критичная линия пересекает математический ландшафт дзета-функции.
Из данных табл. 1 видно, что для нового параметра ряда – прироста простых чисел – такая единственная линия есть. Это – вертикаль 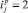 . Покажем, что остальные вертикали для составляющих простых чисел медленно приближаются к критичной линии при условии j → ∞. Тем самым еще раз подтвердим доказательство Харди о том, что в ряду имеется бесконечное множество нетривиальных нулей, часть которых может и не лежать на критичной линии.
. Покажем, что остальные вертикали для составляющих простых чисел медленно приближаются к критичной линии при условии j → ∞. Тем самым еще раз подтвердим доказательство Харди о том, что в ряду имеется бесконечное множество нетривиальных нулей, часть которых может и не лежать на критичной линии.
Для 1 и 2 разрядов (рис. 9) по неразрывным тривиальными нулями вертикалям имеем:
– закон Лапласа (в физике – Мандельброта);
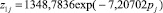 (16)
(16)
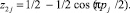 (17)
(17)
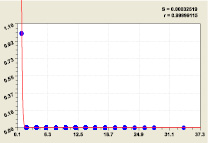
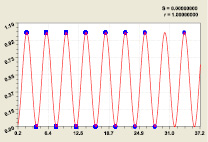
Статистическая модель (16) при первом разряде; Функциональная модель (17) на критичной линии
Рис. 9. Графики распределения двоичного числа у составляющих прироста простых чисел
Критичная линия 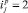 получила однозначную формулу, причем без сдвига волны.
получила однозначную формулу, причем без сдвига волны.
В нашем примере из 500 приростов у простых чисел z6j = 1. Для 3, 4 и 5 разрядов исключаются из вертикалей клетки с тривиальными нулями. Общее уравнение для этих линий получает переменную частоту колебания. Для 3 и 4 разрядов (рис. 10) были получены формулы:
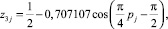 (18)
(18)
совпадает с формулой (7);
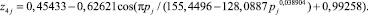 (19)
(19)
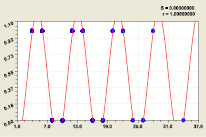
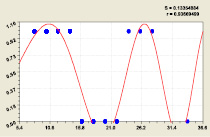
Статистическая модель (18) при третьем разряде прироста; Статистическая модель (19) при четвертом разряде
Рис. 10. Графики распределения двоичного числа у составляющих приростов простых чисел
Еще большее отклонение от критичной линии (рис. 11) происходит на пятом разряде:
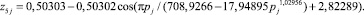 (20)
(20)
Начало критичной линии. Формула (17) соблюдается на минимально короткой критичной линии, содержащей две точки (рис. 12).
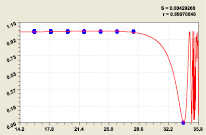
Рис. 11. График (20) распределениядвоичного числа
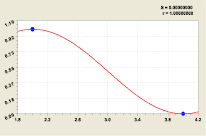
Рис. 12. График двоичного числа двух приростов
Выводы
Знаменитая гипотеза Римана доказана. Для этого было выполнено преобразование ряда простых чисел из десятичной системы счисления в двоичную. Получены четыре новых критерия. Появились геометрические узоры. Стали видны «на полу» нетривиальные нули и появились, вместо крутых «холмов» дзета-функции, единицы «на потолке» распределения 0 и 1.
Библиографическая ссылка
Мазуркин П.М. Расширенное доказательство гипотезы римана // Современные наукоемкие технологии. 2012. № 10. С. 40-47;URL: https://top-technologies.ru/ru/article/view?id=30990 (дата обращения: 03.02.2026).




 двоичной системы
двоичной системы
 двоичный
двоичный