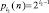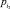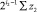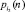Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Мазуркин П.М. 1

---

1 Марийский государственный технический университет

Прирост простых чисел оказался наглядным показателем. Прирост – это количество увеличения, прибавления чего-либо. Если ряд простых чисел образно называют «лестницей Гаусса-Римана», то прирост вполне можно уподобить ступенькам, отделенным от самой лестницы. Доказано, что соблюдается закон на критической линии i2 = 2 второго разряда двоичной системы счисления. Эта функциональная модель оказалась устойчивой и при других количествах простых чисел (3000 и 100 000). Критическая линия Римана расположена в столбце i2 = 2 двоичной матрицы прироста простого числа. Не все нетривиальные нули располагаются на ней. Существуют также линии реперов, первичного прироста (дает узоры симметрии) и огибающей слева двоичные числа 1. Криптографы могут не волноваться: даже на критичной линии прироста простых чисел содержится иррациональное число π = 3,14159... .

Статья в формате PDF

2102 KB

простые числа

прирост

критичная линия

корень 1/2

1. Дон Цагир. Первые 50 миллионов простых чисел. – URL: http://www.ega-math.narod.ru/Liv/Zagier.htm.

2. Гашков С.Б. Системы счисления и их применение. – М.: МЦНМО, 2004. – 52 с.

3. Мазуркин П.М. Биотехнический принцип и устойчивые законы распределения // Успехи современного естествознания. – 2009. – № 9. – С. 93–97. – URL: www.rae.ru/use/?section = content&op = show article&article_id = 7784060.

4. Мазуркин П.М. Биотехнический закон и конструирование адекватных моделей // Успехи современного естествознания. – 2009. –№ 9. – С. 125–129. –

5. Сигнал. URL: http://ru.wikipedia.org/wiki/ %D0 %A1 %D0 %B8 %D0 %B3 %D0 %BD %D0 %B0 %D0 %BB.

Гаусс, Риман и за ними и другие математики увлеклись относительной мощностью x/π(x) простых чисел с усеченным началом, представленным в десятичной системе счисления. При этом, видимо неосознанно, этот показатель был логарифмирован с иррациональным основанием e = 2,71... и тем самым при переходе от степени десяти к его натуральному логарифму произошла ложная идентификация. Она и является главной ошибкой более 150 лет.

Применение ln 10 и ложная идея, что в последующих разрядах десятичной системы количество простых чисел всё время увеличивается примерно на 2,3, основывается на предположение, что 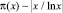. А причина такого поворота в изучении простых чисел была весьма прозаичной. Как отмечается в [1]: «Гаусс, величайший из математиков, открыл этот закон 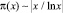в пятнадцатилетнем возрасте, изучая таблицы простых чисел, содержавшиеся в подаренной ему за год до того таблице логарифмов».

Мы отказались от логарифмов, перешли к двоичной системе счисления. Оказалось, что само простое число a(n) = {2, 3, 5, 7, 11, 13, 17, ...}, n = {1, 2, 3, ...} является недостаточно эффективным показателем. Чтобы не было претензий к доказательству, примем этот традиционный ряд.

Прирост простых чисел. Этот новый показатель оказался наглядным и в то же время математически эквивалентным к ряду простых чисел. Прирост – это количество увеличения, прибавления чего-либо. Если ряд простых чисел a(n) = {2, 3, 5, 7, 11, 13, 17, ...} давно образно называют «лестницей Гаусса-Римана», то прирост вполне можно уподобить ступенькам, отделенным от несущей фермы основания лестницы. Длинная и высокая лестница физически вполне может содержать две части – обособленно конструкцию из ступенек и отдельно ферму основания.

Алгоритм наращивания ряда простых чисел. Он, как широко известно, имеет вид

a(n + 1) = a(n) + p(n), (1)

где p(x) – прирост простого числа; n – порядок (порядковый номер) простого числа. Сам ряд простых чисел задан исходно, он определяется условием неделимости на другие числа, кроме на единицу и самого себя (последнее условие даже избыточное).

Поэтому прирост всегда вычисляется вычитанием

p(n) = a(n + 1) – a(n). (2)

500 простых чисел. В табл. 1 даны фрагменты прироста из ряда чисел a(n) = {2, 3, 5, ..., 3571}.

Таблица 1

Ряд прироста простых чисел в 10-й и двоичной системах счисления

Среди 500 простых чисел оказался один максимальный прирост p(217) = 34 для простого числа a(217) = 1327 с кодом 100010 в двоичной системе.

Коренное отличие ряда прироста от самого ряда простых чисел заключается в том, что в приросте (тоже число – абстрактная мера количества) только один столбец i2 = 2 разряда двоичных чисел является полностью заполненным и критичным, а первый разряд имеет только нули для множества a(n) > 2.

Полное заполнение продолжится до бесконечности, поэтому можно считать доказанным факт появление p(n) = 2 при любой мощности a(n).

Математический ландшафт. Для его построения (рис. 1) примем в примере i2 = 1, 2, 3, 4, 5 и исключим те строки, в которых по пяти столбцам находится хотя бы один тривиальный нуль.

Показателем является двоичное число z2 в области действительных чисел (0;1).

Критичная линия. Первая строка в табл. 1 автоматически выпадает из множества. После этого при любой длине ряда простых чисел первый столбец i2 = 1 равен нулю. Тогда каждое значение прироста справа налево начинается от нуля и завершается единицей. А за единицей в виде волновой ломаной линии располагаются только тривиальные нули.

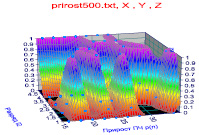
Рис. 1. Ландшафт прироста в ряду из 500 простых чисел

Все нетривиальные нули расположены в любой строке между 1 (слева) и 0 (справа первый столбец). Тогда критическая линия Римана расположена вертикально в столбце i2 = 2. Но становится понятным, что не все нетривиальные нули располагаются на критической линии. Они имеются и в других разрядах двоичной системы вперемежку с тривиальными нулями.

Критичное начало ряда. В табл. 2 показаны три критичных простых числа.

Таблица 2

Прирост критичных простых чисел в начале ряда

Совместно с табл. 1 критичные простые числа дают полный ряд простых чисел, который в данной статье не рассматривается. Чтобы его принять, нужно:

а) признать простым то число, которое делится только на единицу (нуль/нуль неопределенный);

б) изменить порядок в ряде N = {0, 1, 2, 3, 4, ...} ;

в) прирост 1 имеет границу, в некритичный ряд включаются некритичные простые числа P = {3, 5, 7, ...}.

Далее подробный анализ прироста выполним по ряду некритичных простых чисел.

Влияние разряда i2. В программной среде Excel просуммируем по столбцам табл. 1 (без учета первой строки) и получим количество единиц Σz2 по разрядам двоичной системы.

Таблица 3

Влияние разряда двоичной системы счисления (498 строк)

Модели лучше дать по относительным величинам, что позволяет сравнивать между собой разные ряды прироста простых чисел.

После идентификации биотехнического закона [2, 3] были поучены следующие закономерности:

– доли единиц в (рис. 2) строках двоичной матрицы прироста простых чисел

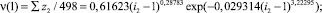(3)

– доли нулей в (рис. 2) строках двоичной матрицы прироста простых чисел

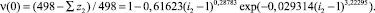(4)

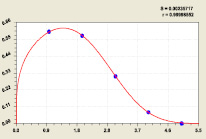
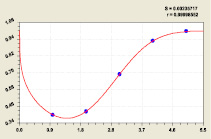
Рис. 2. Доля единиц (слева) и нулей (справа) в строках матрицы: S – дисперсия; r – коэффициент корреляции

В пользу вычислений количества единиц имеются две отличительные особенности:

1) число нулей (тривиальных и нетривиальных) почти в три раза больше единиц (табл. 3);

2) по конструкции формула (2) проще по сравнению с выражением (3).

По-видимому, параметр 0,61623 с ростом ряда n → ∞ будет приближаться к золотому сечению 0,618… . Тогда на критической линии находятся φ–1 = 0,618... единиц и 0,6182 нулей.

Вклад суммы единиц по столбцам (рис. 3) к общей сумме (в табл. 3 773) будет равен

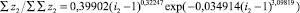(5)

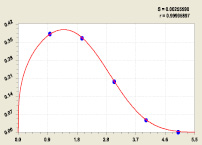
Рис. 3. График вклада суммы единиц по столбцам табл. 1

На критической линии i2 = 2 вклад приблизится к квадрату золотого сечения.

Влияние прироста. За объясняющую переменную берем прирост простого числа. Тогда по разным разрядам двоичной системы счисления образуются свои статистические модели (табл. 4) типа

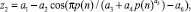(6)

где a1...a6 – параметры модели (6).

Если не учитывать первый и последний разряды двоичной системы, то наиболее близко к рациональному числу 1/2 по вещественным значениям находится разряд i2 = 2.

Для критической линии i2 = 2 формула (6) редуцируется (рис. 4) к виду

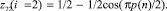(7)

Тем самым полностью доказана гипотеза Римана и снимаем сообщение из Интернета: «А вот знаменитая гипотеза Римана, что вещественная часть корня всегда в точности равна 1/2, ещё никем не доказана, хотя её доказательство имело бы для теории простых чисел в высшей степени важное значение. В настоящее время гипотеза проверена для 7 миллионов корней».

С увеличением мощности простых чисел уравнение (7) для критической линии сохранится, но на графиках типа рис. 4 будут более частые колебания из-за повышения прироста. При этом прирост нарастает гораздо медленнее простого числа. Это даст рост мощности ряда.

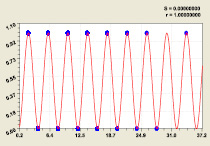
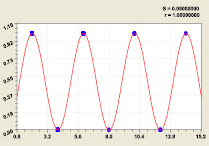
Ряд простых чисел 500; Ряд простых чисел А000040

Рис. 4. Графики формулы (6) для доказательства гипотезы Римана: S – дисперсия; r – коэффициент корреляции

Двоичное число на некритических линиях. В табл. 4 даны параметры уравнения (5).

Для моделирования формулы (5) закономерности z2(p(n)) = f(p(n)) из табл. 1 исключаются те строки, которые имеют в столбце тривиальные нули (пустые клетки). Тогда остается массив из единиц и нетривиальных нулей. С увеличением разряда двоичного числа количество строк в массива z2(p(n)) будет снижаться. Графики приведены на рис. 5.

Таблица 4

Влияние прироста простого числа на двоичное число по разрядам двоичной системы

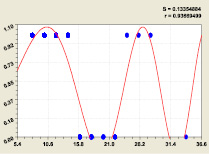
Разряд i2 = 3 двоичной системы счисления; Разряд i2 = 4 двоичной системы счисления

Нули и единицы группируются. Из-за малого количества простых чисел в массиве 500 в столбце i2 = 4 табл. 1, как видно из правого графика на рис. 5, образуются всего две полные группы по четыре элемента. Поэтому формула (5) получает полную конструкцию.

Для разряда i2 = 5 количество групп нулей и единиц (рис. 6) явно недостаточное.

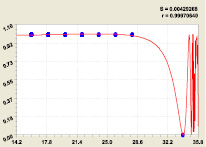
Рис. 6. График формулы (5) для пятого разряда

Наверху образовалась группа из семи единиц, но внизу группа нулей еще только формируется. Поэтому можно определить рациональную мощность ряда простых чисел, обеспечивающую все разряды. Из данных табл. 4 видно, что для i2 = 5 необходимы 710 простых чисел (более 708,9489).

Замечено, что при сокращении массива данных у i2 = 5 до 36 строк характер формул по столбцам i2 = 2 и i2 = 3 не меняется. Это указывает на насыщение у этих двоичных разрядов количества групп единиц и нулей. Они достаточны для идентификации закономерности (6) по параметрам из табл. 4.

Тогда третий разряд с ростом мощности p(n) получает физический смысл по формуле

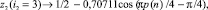(8)

так как сдвиг волны 0,78539815 почти совпадает со значением угла

π/4 = 0,7853975... = 0,7853975… .

Проверка закона

.

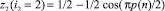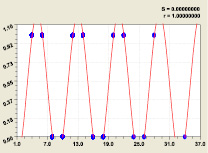
На критической линии i2 = 2 указанная модель устойчива и при других количествах простых чисел (рис. 7).

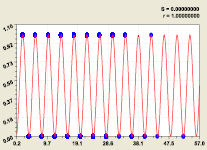
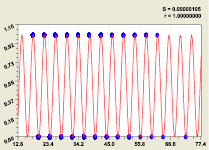
Прирост простых чисел в ряду из 3000 членов; Прирост более 16 в ряде 100 000

С увеличением мощности ряда до 3000 возрастает количество точек в графике (рис. 7). Для проверки было взято подмножество (1704 строки) приростов p(n) ≥ 18 из 100 000 простых чисел. Отсюда следует, что в любой выборке соблюдается наш закон (6) критической линии.

Минимальная выборка простых чисел. Методом отсечения снизу табл. 1 (табл. 5) определим минимальную выборку, где еще действует устойчивый закон критической линии.

Таблица 5

Минимальный ряд простых чисел

Минимальный ряд некритичных простых чисел образуют всего три члена, по которым было получено уравнение (5) с рациональными параметрами, приведенными в табл. 6.

Таблица 6

Влияние прироста простого числа на двоичное число на втором разрядам двоичной системы

Погрешность приближения 0,5 → 1/2 пренебрежимо мала. График простого по конструкции уравнения (6) показан на рис. 8.

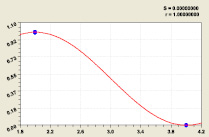
Рис. 8. График формулы (6) для трех простых чисел

У других разрядов i2 > 2 нужно возрастающее количество (мощность) простых чисел. Между приростом и его составляющей существует закономерность перехода чисел из десятичной системы счисления в двоичную.

Реперы. Первые левые единицы образуют асимптотическую линию, левее которой находятся только тривиальные нули. Рассмотрим реперы в ряде из 500 простых чисел.

Репера образуют блоки. В массиве из 500 точек их немного (табл. 7), всего пять.

Исходя из условия, что в начале ряда (табл. 2) прирост равен единице, была получена (рис. 7) формула

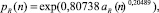(8)

где индекс R обозначает реперное простое число.

Таблица 7

Репера прироста 500 простых чисел

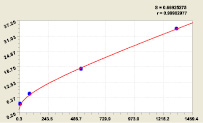
Рис. 9. График реперной функции прироста

Применение реперов гораздо компактнее отношения x/π(x).

Первичный прирост. Это – третий показатель (первый – критическая линия 1/2), дающий картину роста прироста простых чисел.

Параметр pp(n) для ряда из 100 000 простых чисел приведен в табл. 8. Первичный прирост нерегулярен, например, прирост 14 появляется после 8 и раньше значений 10 и 12.

Различным шрифтом выделены треугольники (узоры геометрии) со сторонами (при i2 = 1 – нетривиальные нули). Тогда гармоничные геометрические структуры определяют алгоритм наращивания прироста и даже простого числа.

Таблица 8

Первичный прирост в ряду 100 000

Линия прироста меняется с начальной постоянной «двойкой», а дальше будут колебания, по тренду

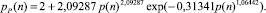(9)

Для условия n → ∞ всегда будет pmin(n) = 2.

Огибающая линия. Приросты левее асимптотической линии имеют тривиальные нули. Поэтому учитывается волновая огибающая линия, которая в разных местах касается критичной линии i2 = 2. Это – четвертый параметр ряда.

Разделим прирост на две части

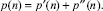
На огибающей линии построчно в таблице (рис. 8) находятся

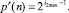
А в блоках

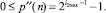
Тренд с единицей из формулы с тремя колебаниями имеет вид

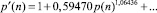(10)

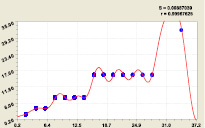
Рис. 10. График огибающей линии прироста 500 чисел

При n → ∞ в формуле (10) всегда будет в начале 1.

Выводы

Критическая линия Римана расположена вертикально в столбце i2 = 2 двоичной матрицы прироста простого числа. Не все нетривиальные нули располагаются на ней. Существуют также линии реперов, первичного прироста (дает узоры симметрии) и огибающей.

Библиографическая ссылка