Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Курков А.А.

К свойствам Вселенной, как внутренности «чёрной дыры», относятся: линейный рост линейных размеров, взаимосвязанный с ним линейный рост массы и постоянство энтропии. Из уравнения для «чёрной дыры», преобразованного с помощью новых констант и соотношений, следует, что энтропия равна квадрату отношения скоростей фотона и гравитона и соответствует отношению количества фотонов к количеству барионов в единице пространства. В данной статье указанные свойства Вселенной служат обоснованием другого взгляда на свойства и светимость космических тел. Получены простые теоретические соотношения излучения света космическими телами. Сопоставление теоретических оценок с наблюдательными данными позволяет говорить об их значимости как законов. Прогноз, выполненный на их основе для планет-гигантов, Земли и космического тела с температурой 2,73 K, дал отличный результат. Это позволяет утверждать, что светимость космических тел – свойство Вселенной.

Статья в формате PDF

475 KB

теория поля

магнитная гравитационная константа

скорость гравитонов

константа структуры

светимость звёзд

В предыдущих работах показано, что приложение теории поля Дж. Максвелла к гравитации позволяет объяснить устройство солнечной системы, вычислить три новые фундаментальные константы и приводит к новому пониманию устройства Вселенной. В новой теории гравитон приобретает свойства пространства, которое однозначно связано с массой. Скорость «распространения» гравитона

существенно меньше скорости света в вакууме С. Для получения непротиворечивого описания Вселенной необходимо потребовать, чтобы пространство и вся Вселенная полностью описывалась двумя фундаментальными взаимодействиями вместе: электромагнитным и гравитационным. В этом случае ядерное взаимодействие и слабое не относятся к фундаментальным. В результате получаем один математический аппарат и два набора фундаментальных физических констант. Такая Вселенная в целом описывается уравнением для «чёрной дыры» и является её внутренностью в том смысле, что границы Вселенной расширяются со скоростью света и вместе с расширяющимся пространством взаимосвязано растёт масса. Поскольку плотность «чёрной дыры» падает по закону R^-2, то логичней искать ей образ среди разряжённых объектов (как наша Вселенная), а не среди сверхплотных (как ядра галактик). Кроме того, для внутренности «чёрной дыры» проще представить «квантовые» принципы её устройства. В результате получаем ограниченную, замкнутую Вселенную, границы которой увеличиваются с постоянной скоростью света и с постоянной скоростью увеличивается её масса. Замкнутая Вселенная должна обладать постоянной энтропией.

Данная статья служит практическим приложением новой теории Вселенной к проблемам изучения звёзд. Покажем наличие постоянной энтропии, воспользовавшись уравнением для «чёрной дыры» и проведя некоторые преобразования, используя новые постоянные и новые соотношения:

или

здесь G_N-K - известная гравитационная константа Ньютона - Кавендиша; G_K = 2,698∙10¹⁹ г/см - «магнитная» гравитационная постоянная; M и R - масса и радиус Вселенной; K = C/VG - константа структуры; λ = M/GK - основная длина волны;  - отношение количества фотонов к количеству барионов в единице пространства Вселенной (см3).

Светимость звёзд современной наукой объясняется происходящими в их недрах ядерными реакциями, но недостаток регистрируемых солнечных нейтрино заставляет задуматься над справедливостью подобного утверждения. Измерения тепловых потоков от Юпитера и Сатурна также свидетельствует об их способности генерировать тепло, в то время как протекание ядерных реакций в них невозможно. Кроме того, аномальные характеристиками свечения квазаров не получили объяснения.

Обратим внимание на фундаментальную постоянную Вселенной - отношение количества фотонов N_γ к количеству барионов N_B в единице пространства и воспользуемся им для обоснования светимости космических тел.

Количество фотонов, излучаемых космическим телом, связано с величиной его поверхности (r - радиус космического тела), температурой T и временем свечения t соотношением:

или в единице объёма космического пространства:

;

здесь R - радиус некоторого объёма космического пространства. Количество барионов в том же объёме пространства связано с массой тела: NB ≈ M. Условность выбора объёма космического пространства позволяет упростить формулу, если воспользоваться законом расширения Вселенной r = (V_G/C)∙R:

Для простоты рассмотрим относительную светимость:

 (1)

здесь T, R и M - параметры звезды уже выражены в единицах относительных к Солнцу. Для Солнца приняты следующие значения параметров: M_o = 1,99∙10³³ г, R_o = 6,96∙10¹⁰ см, T_o = 5770 К, то есть вся зависимость нормирована на соответствующую константу Солнца. Усреднённые параметры звезд главной последовательности приведены в табл. 1.

Вычислим теоретический параметр T3/(M∙R) для каждого класса звёзд главной последовательности табл. 1 и представим его зависимостью от массы звезды (рис. 1).

Таблица 1

Параметры звёзд главной последовательности

Рис. 1 демонстрирует достаточно плотную группировку точек относительно линии уровня 1. Учитывая большую ошибку при измерении физических параметров звезд, предложенный теоретический параметр хорошо согласуется с прогнозом учитывая, что он охватывает весь диапазон звёзд.

Используя данные табл. 1, получим ещё две эмпирические зависимости, которые могут в дальнейшем пригодиться для упрощения полученного теоретического параметра предложенного выше или для вывода некоторых полезных закономерностей о природе и эволюции звёзд.

Первая из предлагаемых зависимостей - линейная зависимость температуры от радиуса (рис. 2), проходящая через 0. Если провести произвольную прямую, то получим регрессию T = 0,7987∙R + 0,1887 (R² = 0,9954).

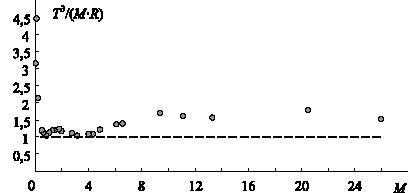
Рис. 1. Зависимость теоретического параметра T3/(M∙R) от массы звезды.
Точки - значения параметра для каждого класса звёзд главной последовательности.
Пунктирная линия - прогноз, равный 1

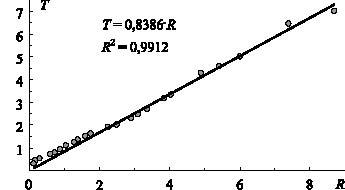
Рис. 2. Зависимость температуры звезды от её радиуса. Исходные данные - точки.
Линия регрессии проведена через 0

Как видно из рис. 2 зависимость T = 0,8386∙R отлично описывает наблюдательные данные, судя по коэффициенту детерминации R² = 0,9912.

Следующая эмпирическая зависимость связывает температуру с массой (рис. 3), что позволит сравнить наблюдение с теорией.

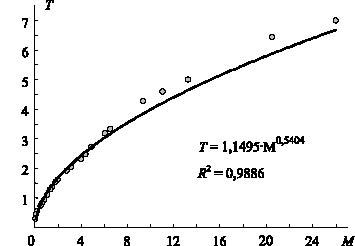
Рис. 3. Эмпирическая зависимость температуры от массы.
Точки - исходные данные, линия - степенная регрессия

Из выведенного теоретического параметра (а он выведен без учёта иерархии структуры Вселенной) следует, что при линейном росте радиуса и массы космического с возрастом, температура тела будет меняться по закону f(t) ~ T ^3/2.

В данной статье используется количество фотонов , а не светимость звезды (количество излучаемой энергии), как принято в астрономии:

.

Радиус звезды вычисляется на основании приведённой формулы для светимости по измеренному значению этой величины и по измеренной температуре звезды в максимуме спектра. Следующее соотношение, которым пользуются астрономы, получено из сравнения масс и светимостей звезд:

(светимость приблизительно пропорциональна четвертой степени массы). К сожалению, эта пропорция имеет ярко выраженную зависимость и перелом при M ≈ 10 M₀. Если использовать количество фотонов, то получится иная зависимость:

(рис. 4).

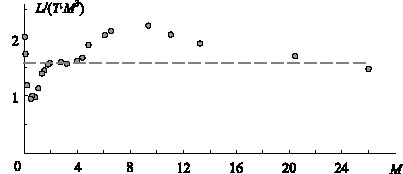
Итак, из свойств Вселенной следует, что с возрастом радиус космического тела линейно растёт и линейно растёт его масса. Увеличение радиуса приводит к тому, что «светимость» единицы поверхности космического тела падает как r-2 (то есть с возрастом), рост массы приводит к увеличению температуры как T ^3/2 (также с возрастом). Учитывая указанные особенности, в удалённых областях Вселенной должны наблюдаться структурированные объекты, искать которые следует в красной и инфракрасной областях спектра.

В табл. 2 приведены параметры планет-гигантов, Земли и тела с температурой в максимуме спектра, равной 2,73 К (M*).

Таблица 2

Параметры планет-гигантов, Земли и тела с температурой
в максимуме спектра, равной 2,73 К

На основании соотношения T³/(M∙R) вычислена температура планет Солнечной системы в Кельвинах (прогноз показан в скобках). Согласие расчётной температуры и наблюдаемой для планет-гигантов хорошее и тем лучше, чем дальше планета от Солнца. Для Земли предсказанная температура значительно меньше наблюдаемой, что связано с освещением поверхности планеты Солнцем.

Температуре T = 2,73 К соответствуют масса и радиус космического тела: М^¤ = 6,6∙10²⁵ г; R = 2240 км, что хорошо согласуется с массами и размерами спутников планет. Возможно, «реликтовое излучение» объясняется светимостью этих самых лёгких космических тел.

Уравнение (1) хорошо показало себя для всего диапазона космических тел, поэтому приведённое соотношение может иметь фундаментальное значение для объяснения светимости и эволюции звёзд.

В предлагаемой теории нет понятия «звезда» - космического тела, которое выделяет энергию благодаря происходящим в его недрах ядерным реакциям. В теории Вселенной всякое космическое тело должно «светить», потому что это свойство Вселенной.

Библиографическая ссылка