Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Герасимов С.А.

Работа представляет собой подробное описание процедуры, особенностей и алгоритма моделирования упругого и неупругого классического рассеяния молекул газа неоднородной поверхностью твердого тела. Предполагается, что твердое тело находится в среде, распределение скоростей молекул которой является изотропным. Алгоритм позволяет изучить механизм воздействия среды на тело практически произвольной формы.

Статья в формате PDF

697 KB

газовая динамика

моделирование

рассеяние

Существует ряд физических задач, которые не могут быть решены ни аналитически, ни численно, ни экспериментально. Одной из таких задач является изучение особенностей многократного рассеяния молекул газа неоднородной поверхностью твердого тела. До сих пор непонятно, какой из каналов рассеяния, зеркальный, диффузный или лепестковый и при каких условиях является доминирующим. Считается лишь, что при тепловом равновесии, то есть тогда, когда распределение скоростей молекул, покидающих поверхность, совпадает с распределением скоростей молекул, прибывающих на эту поверхность, рассеяние молекул является не зеркальным, а диффузным [1]. С другой стороны, диффузный характер рассеяния должен приводить к совершенно непредсказуемым и парадоксальным результатам, одним из которых является появление существенной подъемной силы, действующей на тело, одна из поверхностей которого является шероховатой, а другая - нет [2]. Следует заметить, что при зеркальном рассеянии такое явление отсутствует [3]. Наверное, было бы излишним напоминать, что проверка этих результатов обязательна. Сделать это можно только с применением процедуры моделирования [4]. Идеология моделирования, ее возможности и недостатки хорошо известны [5]. Однако задача многократного классического рассеяния молекул газа неоднородной поверхностью не укладывается в рамки общего подхода, акцентирующего внимание на математических, а не физических проблемах. Недостаточными являются и сведения, относящиеся к моделированию процессов движения и столкновения молекул, ведущему к уравнению Больцмана [6]. Не отличаются подробностью и последние результаты [7], в которых рассмотрено только диффузное рассеяние и только поверхностью достаточно частного вида. Поэтому процедура моделирования многократного рассеяния молекул шероховатой поверхностью твердого тела должна быть подробно описана, разумеется, с максимальным сохранением общности метода.

1. Изотропное, диффузное и зеркальное распределение частиц

Настоящая работа представляет собой попытку решить вполне реальную задачу: шероховатое (неоднородное) тело находится в газовой среде, распределение молекул которой по направлениям движения является изотропным. При этом интерес представляет не только характер траектории классически рассеивающейся частицы, но и некоторые физические параметры, характеризующие взаимодействие молекул с твердым телом. Одним из таких параметров является суммарный импульс, передаваемый всеми молекулами поверхности твердого тела. Это, в свою очередь, налагает определенные ограничения и требования, предъявляемые к моделированию изотропного потока первичных частиц. Совершенно очевидно, что создать модель источника молекул, обеспечивающего изотропное распределение в каждой точке пространства, невозможно. Неудачным кажется и подход, предполагающий изотропное испускание молекул, плоской поверхностью, ограничивающей рассматриваемую часть неоднородного тела. Дело в том, что вычисление телесных углов, с которыми так или иначе придется иметь дело при вычислении передаваемого импульса или давления, в таком варианте решения проблемы представляет ряд совершенно необоснованных трудностей. Более того, пока не ясно, является ли такой подход однозначным. Более последовательным кажется подход, предполагающий экранированное изотропное распределение молекул, падающих на каждый элемент той или иной поверхности твердого тела. Термин «экранированное изотропное распределение» пока не понятен, поэтому должен быть разъяснен. На самом деле полностью изотропным распределением падающих на некоторый элемент поверхности молекул обладают только те молекулы, которые взаимодействуют либо с плоской поверхностью, либо с небольшим уединенным элементом. Даже небольшая кривизна поверхности либо присутствие других частей или поверхностей делают распределение падающих молекул не изотропным. Поэтому под экранированным изотропным здесь понимается распределение только первичных частиц, то есть распределение, для которого

 (1)

справедливо только в ограниченном диапазоне углов.

Пусть (x, y) - координаты элемента поверхности Δs′ нижнего основания неоднородного тела (рис. 1), имеющего полость S, описываемую выражением

 (2)

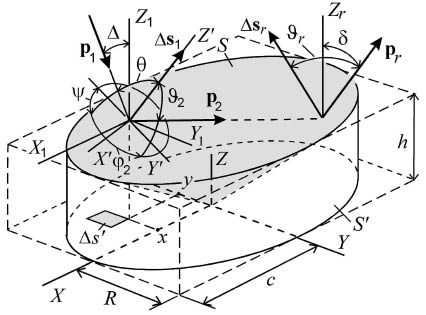
Рис. 1. Геометрия рассеяния

Этим координатам соответствует элемент поверхности полости

 (3)

Пусть p₁ - импульс первичной молекулы, рассеиваемой элементом поверхнос-
ти (3). Поскольку

то для изотропного распределения случайными величинами являются cosq и азимутальный угол ψ. Следовательно, направляющими косинусами траектории первичной частицы (r = 1) в осях X′Y′Z′ являются

 (4)

Диффузное рассеяние (r > 1) подчиняется закону Кнудсена [8], согласно которому молекула газа рассеивается поверхностью внутрь телесного угла dΩ с вероятностью

Это означает, случайными величинами в случае диффузного рассеяния являются cos²θ и азимутальный угол ψ, при этом направляющие косинусы при заданных cosq и y определяются, конечно же, теми же выражениями (4).

При зеркальном рассеянии ситуация намного сложнее, так как параметры рассеянной частицы однозначно связаны с параметрами падающей. Импульс падающей частицы p_r-1 разложим на две составляющие: нормальную -p_Δs и тангенсальную p_τ (рис. 2)

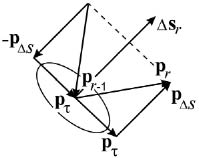
Рис. 2. Зеркальное рассеяние

При зеркальном рассеянии меняется только нормальная составляющая, поэтому импульс рассеянной частицы

Скалярное произведение импульса падающей частицы на нормаль к поверхности дает

Двойное векторное произведение импульса падающей частицы на вектор нормали позволяет вычислить тангенсальную составляющую:

Поэтому импульс рассеянной частицы

а значит

 (5)

 (6)

 (7)

если c′x, c′y , c′z - направляющие косинусы падающей на элемент площади частицы, c_zx, c_zy, c_zz - направляющие косинусы нормали к поверхности и

 (8)

 (9)

2. Преобразование координат

Для определения параметров рассеянной частицы, импульс которой p_r, необходим переход из штрихованной системы координат, связанной и навязываемой элементом поверхности X′Y′Z′, в фиксированной системе XYZ, в которой заданы все параметры неоднородного твердого тела.

Первое, что следует сделать, чтобы осуществить такое преобразование координат, это записать направляющие косинусы осей X′, Y′ и Z′ в системе координат XYZ. Ось Z′ совпадает с направлением нормали к поверхности. Ее уравнение:

 (10)

В знаменателях этого уравнения стоят величины, пропорциональные направляющим косинусам нормали к поверхности, поэтому они должны быть нормированы:

 (11)

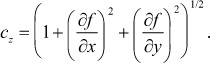 (12)

Для первичных частиц выбор осей X′ и Y′ достаточно произволен, поэтому имеет смысл считать, что угол между осями X′ и Z равен p/2 и, поскольку оси X′ и Z′ взаимно перпендикулярны, то

 (13)

 (14)

чтобы оси X′, Y′ и Z′ соответствовали правой тройке векторов, и из свойств векторного произведения единичных векторов осей:

 (15)

c обязательной нормировкой направляющих косинусов c_yx, c_yy и c_yz.

Теперь направляющие косинусы любой частицы, падающей или рассеянной, в системе координат XYZ определяются преобразованиями

 (16)

 (17)

 (18)

3. Алгоритм и параметры рассеяния

Знание направляющих косинусов рассеянной частицы (16-18), (4) или (5-7) вместе с известным положением элемента поверхности (x, y, z) позволяет при r > 1 проследить дальнейшую судьбу каждой частицы, а при r = 1 смоделировать экранированное изотропное распределение. Для этого для заданного элемента поверхности полости, координаты которого (x, y, z), из всего изотропного потока частиц (0 < ψ < 2π; 0 < cosθ < 1) следует найти координаты пересечения траекторий падающих частиц с плоскостью z = h:

 (19)

 (20)

  (21)

и сохранить для дальнейших анализов и вычислений только те параметры первичных частиц, для которых решения X, Y, Z находятся в области

 (22)

Это и будет экранированное изотропное распределение первичных частиц. Угол D между импульсом падающей частицы и вертикальным направлением Z или Z₁, если это необходимо, определяется выражением

 (23)

При r > 1 следует найти координаты X, Y, Z точки пересечения траектории вторичной частицы

 (24)

с поверхностью

 (25)

то есть решить систему уравнений (24), (25) в области

 (26)

где ε - параметр, имеющий размерность длины много меньший характерного размера рассматриваемой системы. Это условие позволяет исключить из решения системы (24), (25) координаты испускания вторичной частицы. Если решение (X, Y, Z) оказывается за пределами области (22), дальнейший анализ взаимодействия данной конкретной частицы с поверхностью прекращается. Вертикальная компонента импульса частицы, завершившей многократное рассеяние, при этом определяется углом δ:

 (27)

Если вторичная частица попадает на рассматриваемую поверхность, следует координатам (x, y, z) присвоить значения (X, Y, Z), а при зеркальном рассеянии направляющим косинусам c′x,c′y,c′z присвоить значения направляющих косинусов c_xr, c_yr, c_zr, cделать замену r → r + 1 и вернуться к моделированию либо диффузного рассеяния, либо зеркального.

4. Пример

Рамки настоящей работы, ее цель и основной смысл, не позволяют акцентировать внимание на той или иной задаче, которая может быть решена при помощи описанного выше алгоритма. Для диффузного рассеяния одна из таких задач решена. Это - расчет полного импульса, передаваемого молекулами газа твердому телу, одна из поверхностей которого является шероховатой, а другая - нет [7]. Это, правда, сделано только для клинообразной шероховатости. Влияние формы неоднородности на величину передаваемого импульса - предмет специального обсуждения. Здесь же целесообразно продемонстрировать лишь различие между диффузным и зеркальным каналами рассеяния. Это сделано на рис. 3, где показан процесс рассеяния одной и той же молекулы конической полостью при диффузном рассеянии (a) и при зеркальном (b). Совершенно очевидно, что передаваемый при диффузном рассеянии импульс существенно отличается от соответствующего значения при зеркальном рассеянии. Более того, обращает на себя внимание еще один интересный факт. Судя по всему, после большого числа зеркальных рассеяний этот процесс становится плоским, то есть, происходящим только в одной плоскости. А это еще одно подтверждение того, что в процессах с участием только зеркального рассеяния, полный импульс, передаваемый шероховатой поверхности в точности равен импульсу, передаваемому плоскому основанию твердого тела [3]. Теперь можно надеяться, что все претензии и подозрения в некорректности или ошибочности результатов могут быть сняты [9].

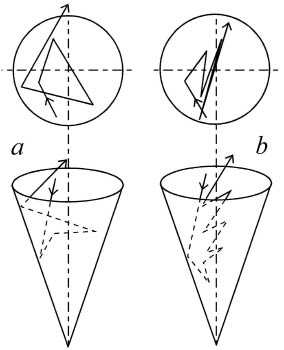
Рис. 3. Два канала рассеяния: диффузный (a) и зеркальный (b)

Список литературы

1. Ролдугин В.И. Физикохимия поверхности. - Долгопрудный: Издательский Дом «Интеллект», 2008. - 568 с.
2. Герасимов С.А. Газодинамическая подъемная сила // Инженерная физика. - 2010. - № 1. - С. 22-24.
3. Герасимов С.А. О левитации и экранировании в газовой динамике // Вопросы прикладной физики. - 2005. - № 12. - С. 131-133.
4. Герасимов С.А. Задача об упругом многократном рассеянии и термолевитации // Учебная физика. - 2005. - №2. - С. 71-81.
5. Михайлов Г.А., Войтишек А.В. Численное статистическое моделирование. Методы Монте-Карло. - М.: Академия, 2006. - 368 с.
6. Берд Г. Молекулярная газовая динамика. - М.: Мир, 1981. - 316 с.
7. Герасимов С.А. Моделирование в проблеме диффузного рассеяния молекул неоднородной поверхностью твердого тела // Динамика сложных систем. - 2010. - Т. 4. - № 2. - С. 25-29.
8. Гудман Ф., Вахман Г. Динамика рассеяния газа поверхностью. - М.: Мир, 1980. - 424 с.
9. Герасимов С.А. Диффузное рассеяние, подъемная сила и второе начало термодинамики // Инженер. - 2010. - № 10. - С. 2-5.

Библиографическая ссылка