С точки зрения факторов активного воздействия все разновидности управления подразделятся на координатное, параметрическое, структурное и смешанное (координатно-параметрическое, координатно-структурное, координатно-параметрически-структурное).
Понятия этих факторов - «координата», «параметр» и «структура» применимы в общем случае как к объекту управления, так и к его средству (модели объекта в том числе). В методическом отношении смысл этих понятий удобно вести от отвечающих им факторов воздействия на модель объекта управления.
Понятия координат, параметров и структуры как факторы воздействия на модель объекта управления
Изначально эти понятия происходят от аналитического - в виде дифференциального уравнения, представления информационной модальности-модели того или иного объекта управления. Происходят в том смысле, что в качестве координат этой модели рассматриваются входная Квх = U и выходная Квых = Y переменные дифференциального уравнения (рис. 1). При этом этимология термин «координата» определяется его синонимом, - соответствующей осью фазового пространства решений этого дифференциального уравнения. Что же касается параметров (здесь, П1, П2, П3) модели объекта управления, то их понятия проистекают от понятий коэффициентов α = П1, β = П2, γ = П3 при переменных и производных переменных Квх = U и Квых = Y дифференциального уравнения
![]()
В свою очередь, в структурной модели объекта управления в случае модели дифференциального уравнения являются отношения его (дифференциального уравнения) координат Квх = U, Квых = Y и параметров α = П1, β = П2, γ = П3. Т.е. получается, что структурой модели объекта управления является её (модели) типаж. Так, в случае модели-дифференциального уравнения таким типажом является класс этого уравнения. В рассматриваемом случае, - класс типа «линейное дифференциальное уравнение 2-го порядка с правой частью». А могут быть ещё такие типажи-классы дифференциальных уравнений, как, например, «система линейных дифференциальных автономных уравнений n-го порядка», «нелинейное уравнение Бернулли», «нелинейное уравнение Риккати» и т.д.
Рассматриваемые понятия координат, параметров и структуры модели объекта управления могут быть проиллюстрированы ещё и на примере её топологического представления (блок-схемы объекта управления) (см. рис. 1), где стрелками обозначены расматриваемые координаты - входная Квх (инвестиции I), промежуточные Кп (координата состояния - количество N произведенных изделий) и выходная Квых (доход D). При этом «начинки» блоков-прямоугольников блок-схемы объекта управления представляют собой параметры его модели П1 (коэффициент выхода годных изделий W) и П2 (цена изделия Ц). Что же касается понятия структуры, то ею, как установлено выше, являются отношения координат и параметров модели объекта управления, в данном случае, - отношения стрелок и «начинок» блоков ‒ прямоугольников блок-схемы объекта управления, т.е. является её конфигурация.
![]()
Рис. 1. Иллюстрация понятий координат, параметров и структуры на примере топологического представления модели объекта управления, где Квх, Квых и Кс - входная, выходная координаты
и координата состояния; S - себестоимость изделия, W - коэффициент выхода годных изделий,
Ц - цена изделия, N - произведенное изделие
Начала координатного и параметрического (координатно-параметрического)управления
Известны два способа придания целевой функции, выходной координате того или иного изменяемого объекта, заданной определённости: регулирование и управление. В системах регулирования и управления эта определённость выражается так называемой уставкой:
- желаемой для выходной координаты объекта функцией;
- желаемым функционалом от функции выходной координаты объекта [экстремумом (максимумом, минимумом), вероятностной мерой (математическим ожиданием, СКО, риском) и т.д.];
- желаемым оператором (например, в том или ином функциональном пространстве) от функции входной и/или выходной координат объекта.
Тогда цель-сущность регулирования и управления может быть выражена, как обеспечение с помощью упомянутых факторов воздействия, - координат, параметров и структуры, максимально соответствующей уставке целевой функции-выходной координаты объекта.
При этом класс операций (регулирование или управление), обеспечивающих означенную цель, определяется задаваемой потребительской разновидностью-характером уставки:
1) Случай уставки-функции:
а) константной - автоматическое регулирование-стабилизация;
б) произвольной известной - программное регулирование;
в) произвольной неизвестной - следящее регулирование.
2) Случай уставки функционала, оператора и т.д. - управление.
Начало широкого распространения регулирования (уставка - константная функция) относится к 1765 году - времени изобретения русским механиком И. Ползуновым первого в мире регулятора питания паровой машины. Позднее были заложены и основы теории регулирования, - Дж. Максвеллом (1868 год) и И. Вышнеградским (1877 год).
Первое средство управления [здесь управления «довинеровского», - адаптации (самонастройки, самоорганизации) на техногенных объектах] - экстремальный регулятор [уставка - функционал (максимум, минимум), фактор воздействия (управляющее воздействие) - координата] было создано во Франции в 1922 году (М. Леблан и Т. Штейн). В СССР первые экстремальные регуляторы появились в 1940 году (Ю. Хлебцевич) и в 1944-1945 годах (В. Казакевич). Позднее, в начале 50-ых годов, Ч. Драйпером и В. Ли (США) были заложены основы теории экстремального регулирования.
В 1948 году понятию управление было придано кибернетическое наполнение - генерализационная работа Н. Винера [1] (Википедия: «Основой теории управления является кибернетика»). Здесь придано кибернетическое наполнение в том смысле, что традиционное управление-адаптация («экстремальное регулирование») было распространено с техногенных объектов Ползунова-Максвелла-Вышнеградского и Леблана-Штейна-Хлебцевича-Казакевича-Драйпера-Ли на объекты живой («био») природы («control...in the animal»). При этом позднее стали применяться и уставки самого общего вида: не только функции-функционалы, но и операторы.
А еще позднее, в 1950-е годы, Ст. Бир [2], У. Эшби, У. Мак-Каллох, Г. фон Фёрстер и Г. Бейтсон распространяют управление Н. Винера с отдельных объектов техносферы и живой (в т.ч. и «ноо») природы на их системы. В пределе - социумы.
При этом если управление Н. Винера, по аналогии с регулированием и управлением-адаптацией осуществлялось по координатам[1] (т.е. являлось координатным, или в этом отношении, - одномерным: «кибернетика 1-го порядка»), то управление Ст. Бира, У. Эшби и др. осуществлялось уже, - в связи с резким (новое качество!) усложнением объектов управления [переходу к социумам (например, отражающим их целенаправленное поведение финансовым потокам)] не только по координатам, но ещё и по параметрам, на этот раз, - уже не только средств, но и объектов управления. При этом, в отличие от винеровского одномерного управления, управление по Ст. Биру, У. Эшби и др. оказывалось уже, таким образом, двумерным - «кибернетика 2-го порядка. При этом критерий перехода от «кибернетики 1-го порядка» к «кибернетике 2-го порядка» дан в [3].
Далее следует отметить, что в Советском Союзе широкомасштабное проведение работ по координатно-параметрическому управлению началось в 1968 году с создания по инициативе акад. Б. Петрова одноименной лаборатории проф. В. Рутковского [4] в Институте автоматики и телемеханики (ИАТ) АН СССР.
О технической реализации параметрического управления
Здесь следует отметить, что переход от операций регулирования-управления (адаптации) к управлению, по Н. Винеру, было ознаменовано введением в теорию управления ещё и информационных представлений. В соответствии с этим обратим внимание на то, что имеющий место объект управления-физическая реалия ‒ является в то же время и носителем информации о самом себе. При этом сущность, семантика, информации об объекте управления содержится, в том числе, и в рассмотренной выше аналитической или топологической его модели. Здесь -
содержится в этой модели и посредством её же и проявлятся, т.е. является во-вне.
Образно эта информация может быть интерпретирована в виде некоего кувшина (рис. 2), где его содержимое, допустим, жидкость, представляет собой семантику-сущность объекта управления, а сам кувшин - форму этой семантики. Здесь - форму как аналитическую или топологическую модель, эту семантику содержащую и проявляющую. Тогда получается, что названные выше параметры и структура модели объекта управления выражаются в параметрах П (размерах) и структуре
С (конфигурации) кувшина (см. рис. 2). Что же касается координат объекта управления, то в случае кувшина аналогами их являются таковые входная Квх, - количество вливаемой в кувшин жидкости, и выходная Квых, - количество жидкости, выливающаяся из кувшина.
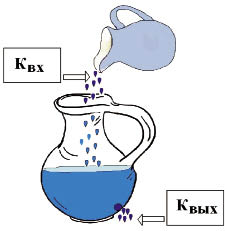
Рис. 2. Интерпретация информации об объекте управления, содержащейся в его модели
Далее - в соответствии с рассматриваемыми аналогиями, получается, что количество содержащейся в кувшине жидкости (выходная координата Квых) зависит как от вливаемой в кувшин жидкости (входной координаты Квх), так и от конфигурации кувшина (структуры С) с её (структуры С) определённостью - размерами-параметрами П.
В результате получается, что в представленной интерпретации координатное управление, по Ст. Биру, У. Эшби и др., заключается в изменении содержащейся в кувшине жидкости, - выходной координаты Квых - посредством изменения размеров кувшина - параметров П. Т.е. получается, что координатное управление по определению - как оно изначально задумано - должно осуществляться непосредственно на самом объекте и, таким образом, в реальном масштабе времени. Это значит, что такое - непосредственно на самом объекте, управление, во-первых, нарушает режим нормальной эксплуатации объекта (необратимость возможных негативных последствий управления), а во-вторых, как реализуемое в реальном масштабе времени, является чрезвычайно медленным в осуществлении и, таким образом, непригодным не только для многократного варьирования параметров П, но и вообще для их варьирования.
Это означает, что подобное, - непосредственно на самом (физическом) объекте управления, манипулирование параметрами П, как управление является нереализуемым на практике.
О необходимости моделирования при параметрическом управлении
Выход - в использовании в контуре параметрического управления вместо самого объекта его модели (рис. 3).
В данном случае на полученной заранее и верифицированной по результатам нормальной эксплуатации объекта управления модели (из соображений максимальной близости к объекту, например - имитационной) в ускоренном, машинном, масштабе времени осуществляется многократное (с помощью компьютера и, например, по методу полного факторного планирования, или, более экономно, ротатабельно [5]) изменение параметров П модели.
Цель - определение таких значений П* параметров П, которые обеспечивали бы требуемую выходную координату Квых объекта управления. Здесь - требуемую выходную координаты объекта управления Квых в том смысле, что в максимальной степени приближенную, как это имеет место при всяком регулировании-управлении, к, - это имеет место уже только при управлении, произвольной (например, экстремальной) уставке К*вых этой координаты.
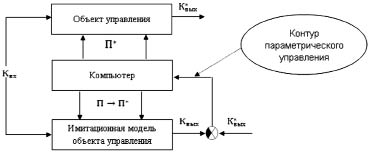
Рис. 3. Блок-схема системы параметрического управления
А далее осуществляется, в режиме советчика, перенос найденных таким образом значений П* параметров модели объекта управления на сам физический объект управления.
Аналогично для задач Ст. Бира, У. Эшби и др. может быть показана такая же необходимость моделирования в контуре структурного управления. А это значит, что такая же необходимость имеет место и при всех возможных сочетаниях параметрического и структурного управления с координатным - координатно-параметрическом, координатно-структурном и др.
Заключение
Возникновение кибернетики в 1948 году ознаменовалось переходом от операций регулирования и управления-адаптации в техносфере к управлению по Н. Винеру - таковому одномерному (координатному) ещё и отдельными объектами живой («био») природы, т.е. ознаменовалось переходом к так называемой «кибернетике 1-го порядка».
В 50-е годы, в связи с вовлечением в сферу кибернетики систем объектов живой (в т.ч., и «ноо») природы, т.е., социумов (Ст. Бир, У. Эшби, У. Мак-Каллох, Г. фон Фёрстер, и Г. Бейтсон), происходит переход от винеровского одномерного (координатно-параметрически-структурное) управления - «кибернетики 1-го порядка», к дву- и многомерному (координатно-параметрическому) управлению, или «кибернетике 2-го порядка».
Такое управление (в частности параметрическое) хотя и должно, но принципиально не может осуществляться на реальных объектах. Оно может осуществляться только на моделях объектов управления (прежде всего имитационных) посредством включения этих моделей в контур управления и использования режима советчика.
Список литературы
- Винер Н. Кибернетика, или управление и связь в животном и машине. - М.: Советское радио, 1958.
- Бир Ст. Кибернетика и управление производством. - М.: Наука, 1965.
- Бондаревский А.С., Лебедев А.В. О «кибернетике второго порядка»: научные основания и критерий применяемости координатно-параметрического управления // Международный журнал прикладных и фундаментальных исследований. - 2010. - №5.
- Петров Б.Н. Рутковский В.Ю. Земляков С.Д. Адаптивное координатно-параметрическое управление нестационарными объектами. - М: Наука, 1980.
- Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. - М.: Наука, 1965.
[1] А ещё, - и по параметрам-структуре. Но...только по параметрам-структуре средств управления (не объек-тов!) - см. ниже.
Библиографическая ссылка
Бондаревский А.С., Лебедев А.В. О НЕОБХОДИМОСТИ МОДЕЛИРОВАНИЯ ПРИ ПАРАМЕТРИЧЕСКОМ УПРАВЛЕНИИ // Современные наукоемкие технологии. 2011. № 2. С. 17-22;URL: https://top-technologies.ru/ru/article/view?id=26672 (дата обращения: 03.02.2026).



