Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Московкин В.М. Билаль Н.Е. Сулейман

Проделан качественный анализ динамической системы третьего порядка, описывающей взаимодействие спроса и предложения на рынке образовательных услуг, и предложенный Л.А. Серковым. Качественное исследование подтвердило ранее полученные теоретические результаты Л.А. Серкова по редуцированным моделям и его численным экспериментам по исходной трехмерной модели. Данная модель была усложнена с помощью замены простейшего релаксационного члена в третьем уравнении динамической системы (отвечающий за процесс качества подготовки специалистов) на логистический член. Это привело к увеличению числа особых точек с 2 до 3 и позволило получить некоторые новые качественные результаты, касающиеся устойчивости особых точек.

Статья в формате PDF

138 KB

математическое моделирование спрос и предложение на рынке образовательных услуг

динамические системы третьего порядка

устойчивость особых точек

В работах В. А. Буланичева и Л.А. Серкова [1, 2] на основе модели Лоренца [3] построена модель самоорганизующейся образовательной системы, описывающей взаимодействие спроса и предложения на рынке образовательных услуг. Для пространственно однородной образовательной системы уравнения имели вид

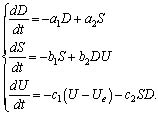
Здесь D - функция спроса на выпускников вуза, S - объем продукта предложения образовательной системы, U - управляющий параметр, связанный с качеством подготовки выпускников вуза (например, отношение числа выпускников вуза, работающих по специальности к среднему значению этого показателя для вузов данной категории).

Первые члены динамической системы являются релаксационными и связаны с затуханиями спроса, предложения и управляющего параметра по мере насыщения рынка труда специалистами соответствующего уровня. Второй член первого уравнения системы (1) связан с взаимодействием рынка труда с образовательной системой и ростом спроса (a₂ - коэффициент спроса). Второй член второго уравнения системы (1) отражает наличие положительной обратной связи между спросом специалистов D и уровнем их качества (b₂ - коэффициент связи). В третьем уравнении управляющий параметр релаксирует к стационарному значению U_e, обусловленному внешним воздействием среды и соответствующему требованиям рынка труда. Такая релаксация происходит, когда S или D (или обе переменные вместе) стремятся к нулю. Наконец, второй член третьего уравнения системы (1) отражает наличие отрицательной обратной связи (c₂ - коэффициент связи), обусловленной тем, что на изменение управляющего параметра отрицательно влияют S и D (ориентация на массовое предложение отрицательно влияет на качество и спрос выпускников).

Все величины, входящие в модель (1), характеризуют поведение системы как целого, то есть представляют значения, усредненные по объему системы (ансамблю всех подсистем и процессов).

Здесь основой синергетического подхода является то обстоятельство, что положительная обратная связь переменных D(t), U(t) с переменной S(t), зависящими от времени, приводит к самоорганизации системы.

Вид динамической системы (1) совпадает с уравнениями Лоренца [1-3], записанными в перенормированных переменных. Запись уравнений Лоренца в форме (1) обусловлена выделением в явном виде параметра U_e, отражающего связь системы с внешней средой и влияющего на самоорганизацию. Этот параметр задает образовательной системе определенные критерии качества учебного процесса.

В дальнейшем с помощью введения в систему (1) времен релаксации и с помощью принципа подчинения быстрых мод медленным [4], в зависимости от соотношения этих времен, были получены различные картины самоорганизации образовательных систем [1, 2].

Так как в работах [1, 2] теоретически рассматривались только редуцированные системы уравнений (динамические системы второго порядка), следующие из трёхмерной динамической системы (1), то рассмотрим подробно эту динамическую систему. Ее особые точки получим в виде:

Характеристическое уравнение для динамической системы (1) запишется в виде

Для первой особой точки это уравнение примет вид

1.

2.

где

Из кубического характеристического уравнения (3) получим:

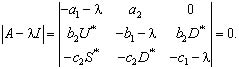 (2)

Если  

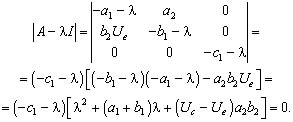 (3)

то λ₂ < 0, λ₃ <0, и приходим к устойчивому узлу (при U_c = U_e имеем λ₂ < 0, λ₃ =0 ).

Если U_c > U_e   , ,  то λ1,2 имеют комплексно-сопряженный вид с отрицательной действительной частью, и приходим к устойчивому фокусу.

Если U_c < U_e , то λ₂ > 0, λ₃ <0, и приходим к седлу.

Для второй особой точки характеристическое уравнение (2) примет вид

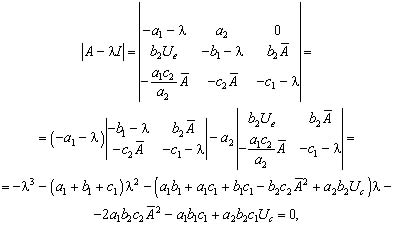 (4)

где  

В окончательном виде уравнение (4) запишем следующим образом

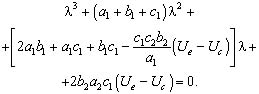(5)

В этом уравнении свободный член больше нуля (U_e > U_c) и изменять знак может только коэффициент при λ.

Применим к уравнению (5) условия Рауса-Гурвица.

Согласно этих условий, для того, чтобы все корни произвольного кубического уравнения

 (6)

с действительными коэффициентами имели отрицательные действительные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица для уравнения (6)

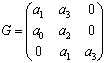 (7)

были положительны:

В нашем случае, эти условия для второй особой точки примут вид

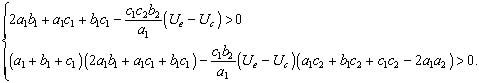
Рассмотрим два частных случая.

1.  откуда следует, что U_c = 1.

В этом случае система неравенств (9) приводится к виду:

2.   

В этом случае система неравенств (9) приводится к виду:

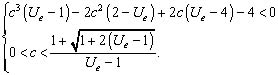 (10)

Посмотрим в какие неравенства перейдет первое неравенство этой системы на границах второго неравенства этой же системы. Легко видеть, что при c = 0 оно удовлетворяется. Подставляя первую границу второго неравенства системы (10) в первое неравенство этой системы, получим

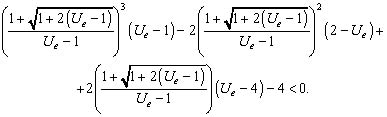(11)

В случае, когда U_e стремится к единицы левая часть неравенства (11) стремится к минус бесконечности, а при возрастании U_e она быстро возрастает. Например, при U_e = 2 оно уже не выполняется. Таким образом, в интервале 1 < U_e < 2 существует некоторое пороговое значение параметра U_e, разделяющее области устойчивости и неустойчивости второй особой точки во втором частном случае. Например, если взять значение , которое использовалось в численных экспериментах с моделью (1) в работах [1, 2], то неравенство (11) примет заведомо выполняющейся вид . Таким образом, в этом случае вторая особая точка является устойчивым узлом, что было показано в результате численных экспериментов в работах [1, 2].

Если вместо релаксационного члена в третьем уравнении динамической систе-мы (1) взять логистический член, то эту систему можно записать в виде

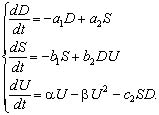(12)

Ее особые точки запишем в виде:

1.

2.

3.

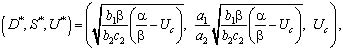
где    - аналог U_e предыдущей задачи.

Характеристическое уравнение для динамической системы (12) запишется в виде

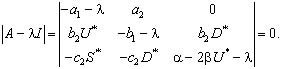(13)

Для первой тривиальной особой точки характеристическое уравнение (13) приводится к виду

и следовательно, приходим к неустойчивому узлу.

Для второй особой точки получим следующее характеристическое уравнение

(14)

которое имеет тот же вид, что и уравнение (3), если в нем положить , . Тогда, если , то приходим к устойчивой особой точке, которая в зависимости от знака неравенства  будет устойчивым узлом или фокусом. В случае, если , то приходим к седловой неустойчивой точке.

Таким образом, для второй особой точки результаты качественного анализа ее устойчивости те же, что и для первой особой точки предыдущей задачи. Характеристическое уравнение для третьей особой точки примет вид

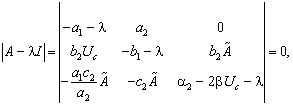(15)

где  

Здесь необходимо рассмотреть два случая:

1.  - совпадает с предыдущим анализом 

2. .

Во втором случае след матрицы A ( ) может равняться нулю, в отличие от первого случая, когда он отрицательный. Характеристическое уравнение (15) приводится к виду

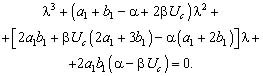(16)

Применяя к уравнению (16) условия Рауса-Гурвица (6-8), придем к следующим условиям на устойчивость третьей особой точки.

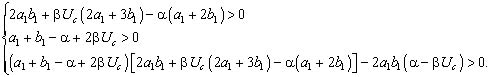(17)

Отметим, что в эту систему неравенств, в отличие от системы неравенств (9), не входит параметр с2 (он входит в координаты особой точки).

Рассмотрим частный случай, когда  . В этом случае система неравенств (17) запишется в виде

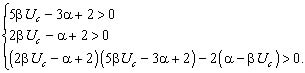(18)

К этой системе неравенств необходимо добавить еще неравенство  (второй случай при рассмотрении характеристического уравнения (15)), которое эквивалентно неравенству

   (19)

Делая замену βU_c = z, рассмотрим систему неравенств (18, 19). Третье неравенство системы неравенств (18) приведем к виду

 (20)

и рассмотрим его на границах интервала (19), который с учетом вышеуказанной замены, преобразуется к интервалу  .

При z = 0 неравенство (20) переходит в неравенство , которое имеет решения , , из которых только первое решение удовлетворяет двум остальным неравенствам системы неравенств (18): , . Этот случай справедлив при предельном переходе , когда

При  неравенство (20) переходит в неравенство α < 2, при этом второе неравенство системы неравенств (18) переходит в тождественное неравенство (2 > 0), а первое - в α < 4. Таким образом, на правой границе неравенства 19) система неравенств (18) удовлетворяется при α < 2, и следовательно, в этом случае третья особая точка динамической системы (12) при a₁ = b₁ = 1 является устойчивым узлом.

Таким образом, в развитие работ [1, 2] мы проделали качественное исследование исходной трёхмерной модели, что подтвердило раннее полученные теоретические результаты В.А. Буланичева и Л.А. Серкова по редуцированным моделям и их численные эксперименты по исходной трехмерной модели. Данная модель была усложнена с помощью замены простейшего релаксационного члена в третьем уравнении динамической системы (отвечающий за процесс качества подготовки специалистов) на логистический член. Это привело к увеличению числа особых точек с 2 до 3 и позволило получить некоторые новые качественные результаты, касающиеся устойчивости второй и третьей особой точки (первая тривиальная особая точка являлась неустойчивым узлом).

СПИСОК ЛИТЕРАТУРЫ

1. Буланичев В.А., Серков Л.А. Модельный подход к функционированию вузов как самоорганизующихся систем // Информационные технологии. - 2006. - № 3. - С. 68 - 73.
2. Серков Л.А. Синергетические аспекты моделирования социально-экономических процессов. - Екатеринбург: ИЭУрО РАН; Изд-во АМБ, 2008. - 216 с.
3. Lorenz E.N. Deterministic Non-periodic Flow // Journal of the Atmospheric Sciences. - 1963. - Vol. 20. - P. 130.
4. Хакен Г. Синергетика. - М.: Мир, 1980. - 404 с.

Библиографическая ссылка