Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Ширма А. А. Чулюков В. А.

Описывается метод улучшения качества изображений посредством попиксельной обработки с применением нейросетевого алгоритма. Представлены первые результаты экспериментов.

Статья в формате PDF

1271 KB

Введение.

Нейронные сети претендуют на то, чтобы стать универсальным аппаратом, решающим различные специфические за­дачи из разных областей в геоинформаци­онных системах. Такая универсальность обусловливается тем, что нейронные сети дают стандартный способ решения мно­гих нестандартных задач. К одной из та­ких задач относится преобразование рас­тровых изображений в векторные графи­ческие модели. Основными достоинства­ми такой модели является возможность масштабирования без потери качества и сравнительно небольшой размер файлов.

Процесс векторизации растровых изо­бражений включает три этапа: предобра­ботка изображения, классификация объ­ектов изображения, оконтуривание клас­сифицированных объектов. В свою оче­редь, одним из компонентов предобработ­ки изображения является улучшение контраста [5].

Методы.

Одним из подходов к улучшению изо­бражений является их обработка в про­странственной области, описываемая уравнением:

где f(x,y) - входное изображение, g(x,y) -обработанное изображение, а T - функция преобразования f определенная в некото­рой окрестности точки (x,y).

Решение этой задачи состоит в ап­проксимации подобной функции, осно­ванной на распределении некоторых статистических характеристик по окрестно­сти каждого элемента изображения.

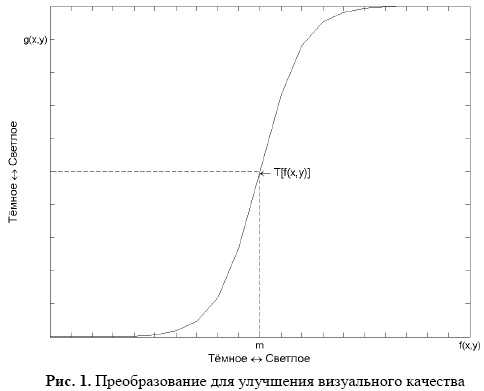
Если T{f(x,y)} имеет вид, показанный на рис.1, то эффект от такого преобразо­вания выразится в получении более высо­кого контраста по сравнению с оригина­лом, а также в затемнении пикселей со значениями меньшими m и повышении яркостей пикселей со значениями большими m на исходном изображении. Этот метод известен, как метод усиления кон­траста [1], а функция T, как «сжимающая» сигмоидная функция, представленная на рис.1 и выражаемая формулой

Обработка   изображения   происходит попиксельно.  Определение  окрестности вокруг точки (x,y) заключается в исполь­зовании квадратной или прямоугольной области S_xy ^Sху . Центр этой области пе­редвигается от точки к точке и для каждо­го нового положения окрестности подсчитывается гистограмма интенсивностей входящих в нее точек.

Для улучшения визуального качества изображения можно использовать некото­рые статистические параметры, получен­ные из гистограмм - математическое ожи­дание m_Sxy, как меру среднего уровня яркости, и дисперсию σ²_Sxy, как меру контраста.

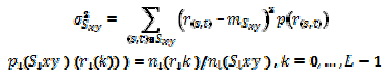
где r_k- значение яркости пикселя -го уров­ня яркости внутри окрестности; p_Sxy(r_k)-вероятность появления пикселя k-го уров­ня яркости внутри окрестности; n_rk - чис­ло пикселей яркости r_k внутри окрестно­сти; n_Sху- общее число пикселей внутри окрестности.

Таким образом, изменение яркости пикселя можно представить в общем виде следующим преобразованием [4]:

где g(x,y) - новое значение яркости пик­селя (x,y) , f(x,y) - старое значение ярко­сти пикселя и M - среднее значение ярко­сти пикселей входного изображения.

К нейронным сетям, решающим зада­чу аппроксимации функций, относятся сети обратного распространения ошибки. В качестве функции активации нейрона подходит вышеописанная передаточная логистическая функция.

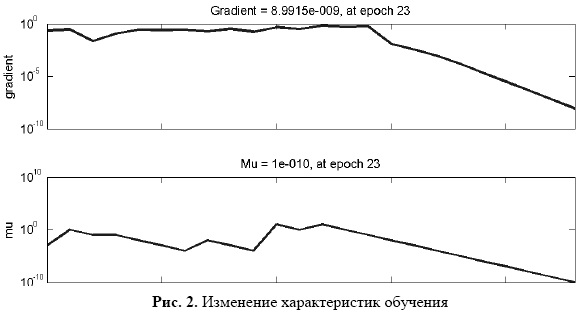
Среди методов, используемых при обучении нейронных сетей, стоит выде­лить алгоритм Левенберга-Марквардта [2, 3], относящийся к классу квазиньюто­новых методов, и, являющийся комбина­цией простейшего градиентного метода и метода Гаусса-Ньютона. Этот алгоритм использует матрицу Гессе приближенно вычисленную, как

а градиент по формуле

где  Е  -   функция ошибки   обучения;

- матрица Якоби производ­ных функционала ошибки по настраивае­мым параметрам, вычисляемая на основе стандартного метода распространения ошибки; e - вектор ошибок сети.

Алгоритм Левенберга - Марквардта использует аппроксимацию гессиана следую­щего вида:

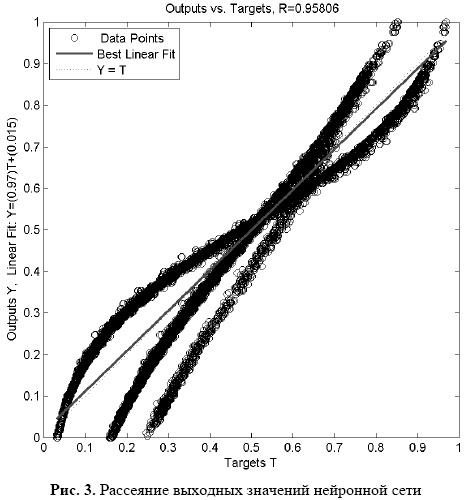
Для оценки отношения между целе­выми и выходными значениями работы нейронной сети используется регрессион­ный анализ (рис. 3). Выходы сети обозна­чены кружками, наилучшая подгонка -пунктирной, а точная - сплошной линией. Линия регрессии отражает распределение выходов нейронной сети, а крутизна её наклона характеризует зависимость меж­ду целевыми и выходными значениями. В данном случае наклон и смещение линии равны соответственно 0.971048 и 0.014768, а коэффициент корреляция 0.958063, что указывает на существенную корреляцию между выходами и целями. Таким образом, можно сказать, что ап­проксимация функции выполнена очень точно.

Для оценивания качества полученного изображения будет использоваться фор­мула Мунтеану-Роса [6]:

 

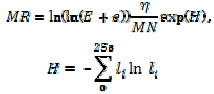
Результаты.

Для экспериментальной проверки предлагаемого метода будем использо­вать следующие алгоритмы и параметры для обработки и оценки изображений:

- однослойная нейронная сеть прямой передачи сигнала с одним нейроном;

-  детектор края Собеля [1];

-  размер области пикселей 3x3;

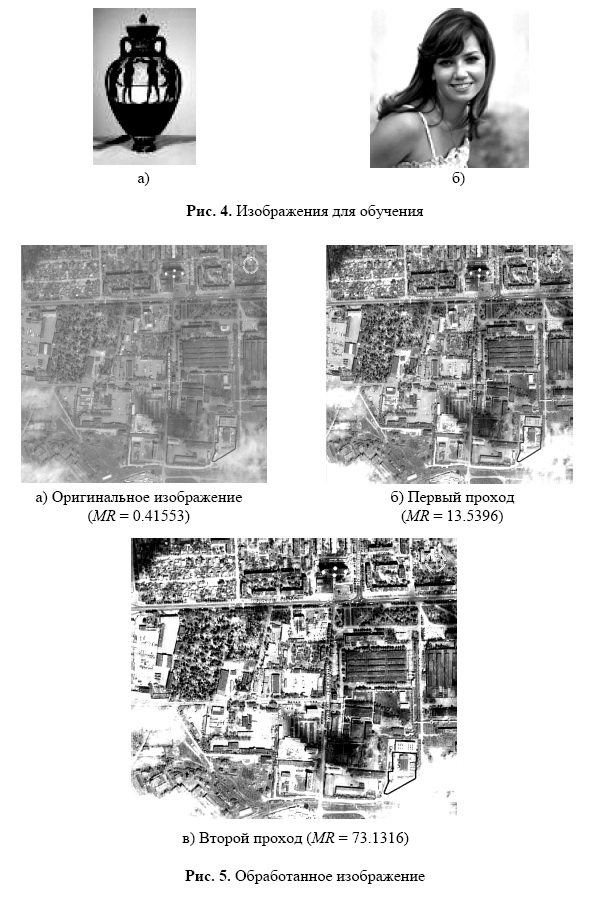
-   для обучения использовались два изображения, размером 65х100 пикселей (рис. 4а) и 120х120 пиксель (рис. 46).

Результат обработки низконтрастного изображения (рис. 5а) географической карты размером 843x981 пикселей с ис­пользованием обученной нейронной сети представлен на рис. 5б,в. Время обучения нейронной сети составило 2.5 секунд.

Время обработки изображения составило 90 секунд. Выводы.

Результаты исследований предложен­ного метода визуального улучшения каче­ства изображений показывают его приме­нимость для решения поставленной задачи.

Работа в данном направлении только начата. В дальнейшем планируются под­робные исследования предложенного ме­тода по следующим направлениям:

-   дальнейшая предобработка изобра­жения, в том числе усовершенствование предложенного метода и обработка изо­бражений с шумами и искажениями;

-   классификация объектов изобра­жения;

-   оконтуривание классифицированных объектов.

СПИСОК ЛИТЕРАТУРЫ:

1. Гонсалес, Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс; пер с англ. под ред. П.А. Чочиа.- М.: Техносфера, 2005. -1070 с.

2. Медведев, В.С. Нейронные сети. Mat-lab 6 / В.С. Медведев, В.Г. Потемкин: под общ. ред. к.т.н. В.Г. Потемкина. - М.: Диалог-МИФИ, 2002. - 496 с.

3. Тархов, Д. А. Нейронные сети. Модели и алгоритмы. / Д. А. Тархов. - М.: Радиотех­ника, 2005. - 256 с.

4. Цой, Ю.Р. Нейроэволюционное улуч­шение качества изображений / Ю.Р. Цой, В.Г. Спицын, А. В. Чернявский // Научная сессия МИФИ - 2006. VIII Всероссийская на­учно-техническая конференция "Нейро-информатика-2006": Сборник трудов. В 3-х частях. Ч.1. - М.:МИФИ, 2006. - с. 181-189.

5. Ширма А.А. Некоторые аспекты векто­ризации изображений. / А.А Ширма, А.А. Чулюков // Междунар. начн.-практ. конф. " Перспективные инновации в науке, образо­вании, производстве и транспорте ´2008": сб.научн.тр. - Одесса: Черноморье, 2008. -Том 2. Технические науки - с.29-31.

6. Munteanu C., Gray-scale image enhance­ment as an automatic process driven 202 by evo­lution / C. Munteanu, A. Rosa // IEEE Trans. on Systems, Man, and Cybernetics - part B: Cyber­netics. - 2004. - Vol. 34, no. 2

Библиографическая ссылка