Оптимальный расчёт технического устройства предполагает выбор варианта, обладающего наибольшими достоинствами, что требует установления критерия оптимальности - целевой функции. При оптимальном расчете устройств для переработки сыпучих сред (смесителей, грануляторов, уплотнителей и других) данная задача является многокритериальной, требующей учета таких важных характеристик как потребляемая мощность, производительность, металлоемкость и др. [1,2]. Из-за сложности формирования такого комплексного критерия на практике может быть использован упрощенный критерий, полностью или частично определяющий упомянутые характеристики. В качестве примера рассмотрим проектирование транспортирующего смесителя с изменяемой формой рабочей поверхности [3] минимальной массы и энергоемкости. Смеситель содержит рабочую ленту с гибкими бортами, огибающую приводные ролики и образующую ячейки смешивания. Смешивание компонентов происходит при их циркуляции в ячейках. Механизм процесса аналогичен, механизму смешивания в барабанном смесителе. В поперечном его сечении можно выделить область обрушения (активного смешивания) и транспортирующую область, прилегающую к рабочей поверхности.
Сформируем целевую функцию из соображений выбора формы ячейки, обеспечивающей наибольшую скорость протекания процесса смешивания. При математическом описании процесса на основе диффузионной модели, скорость его определяется среднестатистическим коэффициентом макродиффузии , известное представление которого в соответствии со статистической теорией взаимодействия дисперсных систем:
![]()
где u´ - хаотическая скорость частиц, τр- характерное время их взаимодействия, D0- постоянный коэффициент, устанавливаемый при идентификации теоретической зависимости коэффициента неоднородности Vc получаемой смеси от времени с результатами экспериментов.
Таким образом, искомый критерий является функцией Z=f(). Для установления структуры коэффициента , исследуемая система моделируется с помощью формализма "перемешивающего биллиарда", в соответствии с которым её динамические характеристики определяются отношением времен пребывания пробных частиц в "фокусирующих" и "рассеивающих" частях биллиарда. Для рассматриваемой системы "фокусирующая" часть моделирует зону активного смешения, а "рассеивающая" - транспортирующую.
Времена пребывания пробных частиц в областях характерного поведения компонентов пропорциональны площадям их поперечного сечения S1 и S2. Влияние геометрии ячейки на процесс определяется критерием, зависящим от амплитуды волны ленты A , образующей ячейку и объема загрузки:
![]()
где Smin- минимальное значение площади поперечного сечения S=S1+S2, при котором начинается циркуляция компонентов, l- длина линии обрушения, разделяющей области поведения материала.
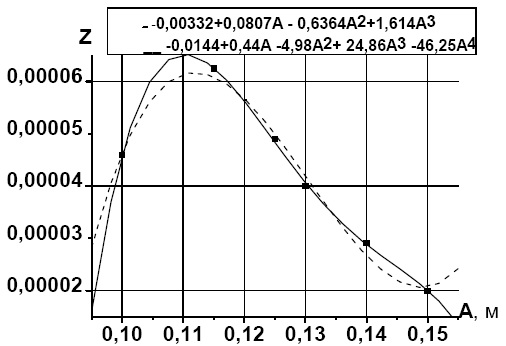
Функция Z, после численных расчетов, аппроксимировалась полиномами третьей и четвертой степени (рис. 1) и максимум её находился методами дифференциального исчисления:Аm=0,110 м.
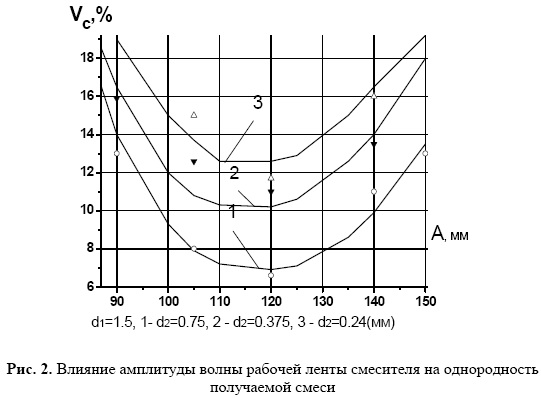
На рис. 2 показаны результаты экспериментальных исследований влияния амплитуды волны ленты (4) смесителя на коэффициент неоднородности Vc смеси.
Исследования проводились для трех смесей с различными средними диаметрами частиц смешиваемых фракций (d1,d2), при прочих фиксированных параметрах системы. Эксперименты устанавливают наличие экстремума в интервале Ат=[0,110/0,125]м, содержащем полученное значение Аm.
Следует отметить, что критерий Z косвенно учитывает параметры мощности, и металлоемкости, поскольку, при заданном значении Vc, позволяет минимизировать длину устройства.
СПИСОК ЛИТЕРАТУРЫ: 1.Таршис Ю.Д., Таршис М.Ю. Основы оптимального и вероятностного проектирования элементов конструкций. Ярославль, 2001. - 387 с.
2.Таршис М.Ю. и др. Новые аппараты с эластичными рабочими элементами для смешивания сыпучих сред. Теория и расчет. Ярославль, 2003. - 84с.
3. А.С.1491732 СССР. Смеситель сыпучих материалов. Опубл. 07.07.1989. Бюл. №25.
Библиографическая ссылка
Таршис Ю.Д., Таршис М.Ю. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ТРАНСПОРТИРУЮЩЕГО СМЕСИТЕЛЯ // Современные наукоемкие технологии. 2009. № 9. С. 40-42;URL: https://top-technologies.ru/ru/article/view?id=26540 (дата обращения: 13.02.2026).



