Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Меньшов Е.Н.

Статья в формате PDF

88 KB

В [1] показано, что математические операторы уравнений Максвелла не удовлетворяют требованиям, предъявляемым к динамическим математическим моделям типа «вход-выход». Поэтому уравнения приводят к противоречию с фундаментальными принципами естествознания: допускают бесконечную мощность энергии поля, нарушают причинно-следственные отношения. Для устранения отмеченных трудностей в [1] предложены скорректированные уравнения Максвелла. Математическая суть: логика математического моделирования привела к необходимости повышения порядка математических операторов левых частей тех уравнений системы Максвелла, которые содержат в себе источники поля. Уравнения для электромагнитных потенциалов имеют вид:

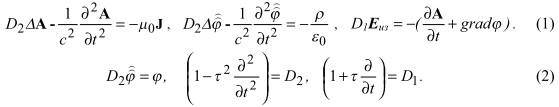
Функция Грина уравнений (1), найденная на основе преобразования Фурье по временной переменной, есть

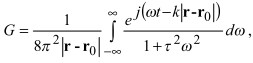 (3)

где R = |r - r₀| - расстояние от точечного источника с координатой r₀ до наблюдателя с координатой r. Интегрируем (3) приближенным методом, разбивая область интегрирования на три участка , в которых применяем следующие аппроксимации:

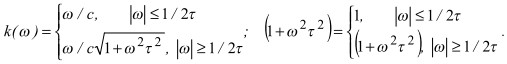(4)

С учетом (4) выражение (3) принимает вид :

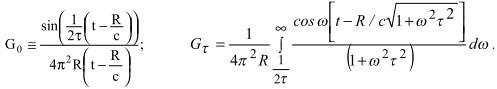(5)

Решения уравнений (1) при произвольных воздействиях будут представлять собой многомерные свертки. Так как G распадается на две составляющие G₀ и G_T, тогда и потенциалы (1) также будут состоять из двух составляющих: Анализ показывает, что G_T не дает излучающих составляющих потенциалов (эти величины пропорциональные R^-2, R^-3), поэтому далее работаем только с G₀.

Для точечного заряда, находящегося в точке r_o(t), с плотностью заряда и плотностью тока соответственно ρ=qδ(R), J=vδ(R) (где δ(R) - дельта функция Дирака, v-вектор скорости) потенциалы выражаются так:

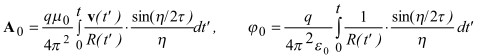(5)

Для определения излучающих составляющих E и H используем следующее допущение - заменяем импульсную функцию (sin(η/2τ))/η идеальным прямоугольным импульсом: если |η|>π τ и, интегрируя (5), получаем:

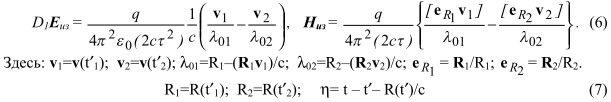
Значения интегралов (5) будут зависеть от степени перекрытия интервала интегрирования с интервалом существования импульсной функции, которую можно установить по третьему уравнению (7). По этой причине поле излучения (6) будет проявлять различные свойства в различных областях изменения R и t.

При малых

Для , поле пропорционально: -v(t)/R(t)≅- a(t)t/R(t), где a(t)-ускорение. Каждая точка этой области одновременно генерирует поле с весовым коэффициентом 1/R. Со временем интенсивность поля возрастает.

Для , поле пропорционально: v₁/R₁-v(t)/R(t). На этом этапе подключается точечный источник из запаздывающего центра, соответствующего прошлому местоположению заряда. Излучение этого источника переносится со скоростью света. Фаза этого источника противоположна фазе распределенного источника, поэтому при прибытии этого поля стремительное накопление интенсивности поля в каждой точке приостанавливается. На границе области распределенного источника интенсивность поля наибольшая, обусловленная максимальным временем запаздывания:

При больших Излучение в этой области изменяется только за счет переноса поля из области его генерации. Выделим три этапа.

Для 0≤ t ≤ t_мин = R(0)/c - πτ интегралы (5) равны нулю, поле отсутствует.

Для волна достигает зафиксированного рубежа и начинается формирование её пологого фронта, поле пропорционально величине -v₂/R₂.

Для Здесь интенсивность поля определяется разностью скоростей, обусловленных разностью запаздывающих моментов времени (t´₂-t´₁)≅ t´₂(t_мак). При R→∞, R(t´₁)≅R(t´₂)=R поле пропорционально: (v₁- v₂)/R ≅-2π τa(t)/R.

Вывод. Физическая суть новых уравнений Максвелла заключается в том, что в них заложено свойство инерционности возбуждения ЭМП при любом источнике возбуждения (полем, зарядом).

[1] Меньшов Е.Н. Новые уравнения Максвелла: преодоление внутреннего противоречия в классической электродинамике// Современные наукоемкие технологии. - 2005. - №1: материалы заочн. электрон. конф. Акад. Естествознания, 20-25 ноябр., 2004 г. - С.89-90.

Библиографическая ссылка