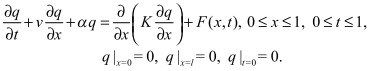
В рассматриваемой модели предполагается, что на границах области находятся поглотители примеси, например, водоемы и на начальный момент времени загрязняющая примесь в области отсутствует.
Прямая задача состоит в определении поля концентрации q( x, t) при заданных условиях. Обратная задача об источнике состоит в отыскании F (x, t) по заданному полю концентрации q(x, t) .
Пусть F (x, t) представима в виде F (x, t) = f (x) g (t), где f (x) - функция, характеризующая расположение источников и g (t) - интенсивность действия источников.
Рассмотрим обратную задачу об источнике с переопределением в точке. Будем искать g (t) при известной функции f (x) и дополнительном условии - переопределении в точке q |x=x* = φ (t). На практике это означает, что в некоторой точке установлен датчик, замеряющий концентрацию примеси.
Наложим ограничения на функцию f (x) : f (x*) ≠ 0, т.е. точка замера находится в зоне действия источника, f (x) ∈ C2 [0,1] и f (0) = f (1) = 0. Известно, что так поставленная обратная задача является корректной [3].
Для упрощения этой задачи был осуществлен переход к новой функции ![]() . Такая замена приводит к нагруженному уравнению:
. Такая замена приводит к нагруженному уравнению:
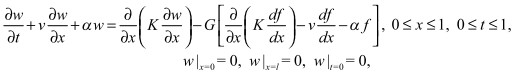
где ![]()
Проведены квазиреальные эксперименты: при известных f (x) и g (t) решается прямая задача и находится концентрация в точке замера, а затем решается обратная задача при известной функции f (x) и вычисленной функции φ (t) в точке замера. Для численного решения прямой и обратной задач в программе была использована явная схема по временной переменной и неявная схема по пространственной переменной. Квазиреальные эксперименты проводились для различных функций f (x) и g (t).
Для проверки устойчивости полученного численного решения g (t) в концентрацию в точке замера была внесена ошибка, случайно распределенная по нормальному закону. В среднем качественная картина поведения восстановленной функции g (t) осталась прежней.
Таким образом, в ходе квазиреальных численных экспериментов было показано, что сформулированная выше специальная обратная задача для источника имеет устойчивое численное решение.
Кроме того, был рассмотрен случай наличия нескольких точек замера концентрации загрязняющей примеси. В ходе численных экспериментов обнаружено, что при разумном расположении точек замера, результаты для нескольких датчиков всегда лучше, чем для одного.
Рассмотрим обратную задачу об источнике с финальным переопределением. Будем искать функцию f (х) по известной функции g(t) и дополнительному условию - финальному переопределению q |t=1= ψ (х) . Такую задачу можно трактовать как задачу точечного управления или как задачу типа "прогноз-управление" [3].
Для поставленной задачи проведены квазиреальные эксперименты: при известных f (х) и g (t) решается прямая задача и находится концентрация в финальный момент времени ψ (х) = q( х,1), а затем решается корректная обратная задача при известных функциях g (t) и ψ (х) [3].
Проведены численные эксперименты для различных конфигураций функции f (х) . Была промоделирована ситуация с добавлением в финальное измерение случайной ошибки. При этом уменьшение дисперсии ошибки влекло уменьшение погрешности при восстановлении функции f (х), что указывает на устойчивость численного решения сформулированной задачи.
Решение рассмотренных в работе обратных задач может быть использовано для минимизации вреда от загрязняющих источников путем их оптимального размещения.
Список литературы
- Марчук Г.И. Математическое моделирование в проблеме окружающей среды. М.: Наука, 1982
- Берлянд М.Е. Прогноз и регулирование загрязнения атмосферы. Ленинград: Гидрометеоиздат, 1985.
- Karmazin W., Lebedinzew W., Karmazin A. Die inverse Aufgabe fur die Gleichung der Turbulenz diffusion// Environmental Problems and Ecological Safety: Proceedings of a workshop held at the University of Applied Sciences Wiesbaden, Germany, September 29 - October 1, 2004. Wiesbaden: Fachhochschule Wiesbaden, 2004. с.116-121.
Библиографическая ссылка
Кармазин В.Н., Лебединцев В.Н., Кармазин А.В. ОБРАТНЫЕ ЗАДАЧИ ОБ ИСТОЧНИКЕ ЗАГРЯЗНЕНИЯ // Современные наукоемкие технологии. 2005. № 11. С. 47-48;URL: https://top-technologies.ru/ru/article/view?id=26433 (дата обращения: 09.03.2026).



