Игра №1: Пусть имеется три шкатулки, в одной из которых находится приз. Предлагается выбрать шкатулку с призом. После того, как игрок делает свой выбор, ему открывают одну из двух других шкатулок, которая заведомо оказывается пустой. После этого спрашивают, не хочет ли он изменить свой выбор?
На первый взгляд может показаться, что вероятность выигрыша в такой ситуации равна 0,5. Однако, вероятность выигрыша зависит от выбранной стратегии. В данной игре возможна одна из трех стратегий:
Стратегия №1: Выбор обязательно меняют.
Стратегия №2: Выбор оставляют неизменным.
Стратегия №3: Случайным образом либо оставляют выбранную шкатулку, либо меняют свой выбор (другими словами отсутствие стратегии).
Решить эту задачу можно аналитически, используя формулу полной вероятности, либо сделать математическое моделирование, т. е., применяя датчик равномерно распределенных случайных величин, разыграть различные стратегии поведения в игре и пронаблюдать частоту выигрыша. Решим задачу по формуле «полной вероятности», для чего введем гипотезы:
Н1- первоначально выбрана шкатулка с призом,
Н2 - первоначально выбрана шкатулка без приза
Вероятности этих гипотез: р(Н1) = 1/3, р(Н2) = 2/3
Событие А - окончательно выбрана шкатулка с призом.
Р(А/Нi) _ условная вероятность появления события А при условии, что произошла гипотеза Н. Как раз эти условные вероятности и меняются в зависимости от выбранных стратегий, что влечет за собой изменение полной вероятности события А, которая рассчитывается по формуле:
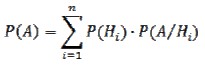
Вычислим вероятность события А при различных стратегиях ведения игры.
Стратегия №1: Выбор шкатулки обязательно меняют
|
Гипотезы Ні |
Р(Ні) |
Р(А/Ні) |
Р(Ні) * Р(А/Ні) |
|
Н1 - первоначально выбрана шкатулка с призом, |
Р(Н1) =1/3 |
Р(А/Н1) = 0 |
1/3*0 = 0 |
|
Н2 - первоначально выбрана шкатулка без приза |
Р(Н2) =2/3 |
Р(А/Н2) = 1 |
2/3*1 = 2/3 |
|
|
|
|
Р(А)=0+2/3 = 2/3 |
Стратегия №2: Выбор шкатулки оставляют неизменным.
|
Гипотезы Ні |
Р(Ні) |
Р(А/Ні) |
Р(Ні) * Р(А/Ні) |
|
Н1 - первоначально выбрана шкатулка с призом, |
Р(Н1) =1/3 |
Р(А/Н1) = 1 |
1/3*1 = 1/3 |
|
Н2 - первоначально выбрана шкатулка без приза |
Р(Н2) =2/3 |
Р(А/Н2) = 0 |
2/3*0 = 0 |
|
|
|
|
Р(А)=1/3+0=1/3 |
Как видим, правильный выбор стратегии, увеличивает вероятность выигрыша в два раза. Для расчета вероятности выигрыша, при отсутствии четкой стратегии, т. е. с вероятностью 0,5 выбор оставляют, и с вероятностью 0,5 меняют, гипотезы введем следующим образом:
Стратегия №3: Окончательный выбор осуществляется случайным образом.
|
Гипотезы Cj |
P(Ci) |
P(A/Cj) |
P(Ci)*P(A/Ci) |
|
C1 - выбор меняют |
P(C1) = 1/2 |
P(A/C1) = 2/3 |
1/2*2/3=2/6 |
|
C2 - выбор оставляют |
P(C2) = 1/2 |
P(A/C2) = 1/3 |
1/2*1/3 = 1/6 |
|
|
|
|
P(A) = 2/6+1/6 = 1 |
Таким образом, теоретическая вероятность выигрыша при отсутствии четкой стратегии равна 0,5. В реальной же ситуации, вероятность, с которой человек оставляет или меняет свой выбор, зависит от личных качеств и заключена в диапазоне
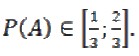
Игра №2: Добавлена четвертая пустая шкатулка, после выбора, открывается заведомо пустая шкатулка и из оставшихся трех предлагают выбрать шкатулку с призом.
Рассчитаем вероятности выигрыша в зависимости от выбранных стратегий:
Стратегия №1: Выбор шкатулки обязательно меняют.
|
Гипотезы Ні |
P(Hi) |
P(A/Hi) |
P(Hi) * P(A/Hi) |
|
Н1 - первоначально выбрана шкатулка с призом, |
P(H1) =1/4 |
P(A/H1) = 0 |
1/4*0 = 0 |
|
Н2 - первоначально выбрана шкатулка без приза |
P(H2) =3/4 |
P(A/H2) = 0,5 |
3/4*0,5 = 3/8 |
|
|
|
|
P(A)=0+3/8 = 3/8 |
Стратегия №2: Выбор шкатулки оставляют неизменным.
|
Гипотезы Ні |
P(Hi) |
P(A/Hi) |
P(Hi) * P(A/Hi) |
|
Н1 - первоначально выбрана шкатулка с призом, |
P(H1) =1/4 |
P(A/H1) = 1 |
1/4*1 = 1/4 |
|
Н2 - первоначально выбрана шкатулка без приза |
P(H2) =3/4 |
P(A/H2) = 0 |
2/3*0 = 0 |
|
|
|
|
P(A)=1/4+0=1/4 |
Как видим, и в этой ситуации изменение своего выбора увеличивает вероятность получения приза, хотя и не столь значительно, как в первой игре.
Следующую игру можно наблюдать в некоторых телевизионных викторинах: предлагается вопрос и к нему четыре варианта ответа, один из которых верный. Если игрок абсолютно некомпетентен в данном вопросе, он может выбрать подсказку «50 на 50», т.е. снять два неверных ответа и производить выбор из двух оставшихся вариантов ответов, один из которых верен. Рассмотрим, позволит ли в данной игре применение стратегии, увеличить вероятность угадать верный ответ? Игрок делает первоначальный случайный выбор одного из ответов, после чего просит снять два неверных ответа. После этого, если выбранный им ответ остался, игрок может придерживаться стратегии «настаивать на своем выборе», если же выбранный ответ снят, то игрок случайным образом выбирает из двух оставшихся. Вероятность угадать при применении стратегии «настаивания на своем» в этом случае составит 0,5, как и в случае, случайного выбора из двух оставшихся ответов. Таким образом, применение стратегий в данной игре не увеличивает вероятность выигрыша.
Библиографическая ссылка
Егоров Ю.В., Егорова Т.П. ИГРОВЫЕ СТРАТЕГИИ // Современные наукоемкие технологии. 2009. № 4. С. 60-61;URL: https://top-technologies.ru/ru/article/view?id=26316 (дата обращения: 17.11.2025).



