Распознавание подразумевает проработку широкого комплекса задач, начиная от оцифровки аналоговой информации и заканчивая ее семантической интерпретацией. В этот комплекс обязательно входит последовательное, параллельное или иерархическое решение классификационных задач.
Решение задач классификации имеет самостоятельное значение для корпоративных систем управления, экспертных систем в медицине и экономике при распознавании различных ситуаций, когда по набору заданных признаков (факторов) выявляется сущность некоторой ситуации, в зависимости от которой выбирается определенная последовательность действий. Для этих задач характерны следующие предметные области.
- Интерпретация данных - выбор решения из фиксированного множества альтернатив на базе введенной информации о текущей ситуации.
- Контроль - отклонение в данных о текущей ситуации от плановых целей и нормативов.
- Диагностика - выявление причин, приведших к возникновению ситуации.
- Коррекция - диагностика, дополненная возможностью оценки и рекомендаций действий по исправлению отклонений от нормального состояния рассматриваемых ситуаций.
- Проектирование - определение конфигурации объектов с точки зрения достижения заданных критериев эффективности и ограничений.
- Прогнозирование - предсказание последствий развития текущих ситуаций.
- Мониторинг - контроль с возможной последующей коррекцией. Для этого выполняется диагностика, прогнозирование.
- Управление - мониторинг, дополненный реализацией действий в автоматических системах.
Предлагается три типа верифицированных алгоритмов обучения на ограниченных бесконечных множествах. Первые два основаны на обучении с учителем третий может стать основой новой теории кластерного анализа без поиска центра кластера.
Rn- действительное n-мерное пространство элементов x=(x1,x2,...,xn), y=(y1,y2,...,yn);
- минимальное расстояние между двумя множествами A и B;
Исключение избыточного признак целесообразно, если δв новом пространстве связано с δ0 в предыдущем следующим соотношением:
для алгоритмов первого
типа
для алгоритмов второго
типа
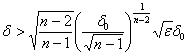для алгоритмов
третьего типа
Аналогично, добавление нового признака оправдано, если:
для алгоритмов первого
типа
для алгоритмов второго
типа
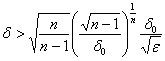для алгоритмов
третьего типа
Главный недостаток алгоритмов первого типа - результат классификации получается на последних шагах работы алгоритма. Мы его потеряем, если есть ограничения по памяти и времени работы.
Недостаток алгоритмов второго типа - равномерная сходимость. Чем больше шагов, тем меньше они отличаются друг от друга. Отработав 50% времени, мы получаем примерно 50% объема, не обработанного единичного гиперкуба. Достоинство - полиномиальная оценка объема памяти.
Достоинства алгоритмов третьего типа - хорошая сходимость, естественность ( не проанализированная область гиперкуба находится вблизи разделяющей два множества границы, распознавание может идти параллельно обучению в фоновом режиме,. Отработав 20% времени в двухмерном пространстве, остальные 80% алгоритм затратит на удвоение δ0. Недостаток - экспоненциальная оценка объема памяти. Поэтому необходимо использовать понятие чувствительности и применять алгоритмы первого и второго типа к непроанализированной части гиперкуба.
Для алгоритмов второго типа время распознавания 
Для алгоритмов первого типа время распознавания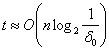 
Для алгоритмов третьего типа время распознавания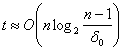 
Возникает вопрос, нужен ли 
?
В многомерных пространствах (100,1000...) чаще будет встречаться ситуация 
, и это нужно учитывать при проектировании алгоритмов.
Понятие проекции в алгоритмах первого и второго типа позволяет решать задачу минимизации числа признаков (сокращение неинформативных признаков, не изменяющих количество ячеек) без вычислений по формулам.
Алгоритмы второго и третьего типа могут быть модифицированы для решения задачи дообучения без пересмотра всего обучающего множества. В этом случае обучение и распознавание сливаются в один процесс, качество которого повышается с течением времени, а распознавание начинается с одного элемента обучающего множества. Для алгоритмов первого типа в этом случае задача обучения решается заново.
Полученные оценки для большого описания множеств
оправдывают следующий порядок использования алгоритмов. В качестве первого
необходимо использовать алгоритм второго типа, его результаты являются входными
данными для алгоритма первого и третьего типа. Их главное отличие друг от
друга: первый тип строит разделяющую границу между двумя множествами
(в некоторых случаях этого вполне достаточно), третий тип - оболочки
разделяемых множеств. Незначительное увеличение времени классификации является
небольшой платой за дальнейшую работу с множествами
как самостоятельными объектами с минимальным описанием. Для получения
такого описания потребуются результаты работы алгоритма первого типа.
Общее достоинство теории: для каждой ячейки может быть индивидуально выбран алгоритм и принято решение об изменении пространства признаков. Что в целом позволяет говорить не только о динамическом изменении пространства признаков, но и о динамическом изменении применяемых алгоритмов. Общим критерием изменения пространства признаков (алгоритмы первого и второго типа) можно считать излишнее дробление R1 или, другими словами, количество дочерних листьев (по R1) значительно превосходит количество классов.
СПИСОК ЛИТЕРАТУРЫ
1. Тетерин А.Н. Геометрический подход к классификации - новая модель работы нейрона.//ЖВМ и МФ. 1992. Т 31. № 12. С. 1972-1980.
Библиографическая ссылка
Тетерин А.Н. ОПТИМИЗАЦИЯ КОЛИЧЕСТВА ПРИЗНАКОВ И МИНИМИЗАЦИЯ ОПИСАНИЯ РЕШЕНИЯ В ЗАДАЧАХ КЛАССИФИКАЦИИ (РАСПОЗНАВАНИЯ ОБРАЗОВ) // Современные наукоемкие технологии. – 2009. – № 11. – С. 43-45;URL: https://top-technologies.ru/ru/article/view?id=25944 (дата обращения: 21.11.2024).