1. О С-точных парах переменных и сюръективности отображений ![]()
Пара (m, k) натуральных переменных m∈ A и k∈ B называется [1] С-точной парой, если для каждых соседних в Е ![]()
![]() ⊆N элементов m и k найдётся число С такое, что
⊆N элементов m и k найдётся число С такое, что
|m-k|<C. (1)
Пусть ξ ![]()
![]()
![]() ,
, ![]()
![]()
![]() и
и ![]() . Пусть далее, Ni
. Пусть далее, Ni ![]()
![]() и Di
и Di ![]() Ni |φ (Ni ). Функция φ: N→N и ξ определяют последовательности {δi } и {di },
Ni |φ (Ni ). Функция φ: N→N и ξ определяют последовательности {δi } и {di }, ![]() , где δi
, где δi ![]()
![]() {φ(n)- ni } ≥ 0 и di
{φ(n)- ni } ≥ 0 и di ![]() |Di | ≥ 0. Очевидно, что условие ∃ξ
|Di | ≥ 0. Очевидно, что условие ∃ξ ![]() di = 0 является достаточным для сюръективности отображения φ. Примеры показывают, что это условие не является необходимым. Функция
di = 0 является достаточным для сюръективности отображения φ. Примеры показывают, что это условие не является необходимым. Функция ![]() определяет последовательность {
определяет последовательность {![]() }, n∈N, целых чисел
}, n∈N, целых чисел ![]()
![]() φ(n)-n. Очевидно, что если
φ(n)-n. Очевидно, что если ![]() и
и 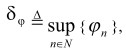 , то
, то ![]() Но существует пара (x, ) такая, что
Но существует пара (x, ) такая, что
δξ = δφ. (2)
Доказаны с использованием, в частности, (2) следующие предложения.
Утверждение 1. Для инъекции φ: N→N справедливо следующее условие:
![]() (3)
(3)
Утверждение 2. Если φ: N→N, то ∃ C, С ≥ 0:
![]() (4)
(4)
Утверждение 3. Если φ: N→N, то
![]() , или, что эквивалентно, Ni ⊂ φ ( Ni+j ). (5)
, или, что эквивалентно, Ni ⊂ φ ( Ni+j ). (5)
Теорема 1. Условия (4) и (5) являются независимыми необходимые условиями сюръективности инъективного отображения φ: N→N, а их совместное выполнение является достаточным условием сюръективности этого отображения.
Утверждение 4. Из условия (3) следует, что для любой последовательности ξ существует число ![]() такое, что
такое, что ![]()
![]()
Утверждение 5. Для всякой пары (m, k) переменных ![]() существует число С>0 такое, что пара (m, k) является С-точной парой (1).
существует число С>0 такое, что пара (m, k) является С-точной парой (1).
Следствием Теоремы 1 является [1, c. 89]
Теорема 2. Не существует биекции между множеством N и его собственным подмножеством.
2. Приложения понятия С-точной пары переменных
Определение 1. Числовая последовательность (а) называется (ср. [1, c. 98]) w-сходящейся последовательностью (widely convergent sequence - w-CS), если:
![]() (6)
(6)
С помощью понятия С-точной пары (1) и условия (6) доказано, что множество {w-CS} совпадает с множеством {FS} фундаментальных последовательностей (последовательностей Коши). Не ограниченная конечным числом последовательность Коши ![]() сходится, по определению [1, c. 100], к бесконечно большому числу (ILN) Ω(а). Например, последовательность
сходится, по определению [1, c. 100], к бесконечно большому числу (ILN) Ω(а). Например, последовательность ![]() для α>0 является w-CS, так как
для α>0 является w-CS, так как
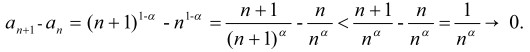
Переход от теории числовых последовательностей к анализу даёт [1, c. 101]
Теорема 3. Неограниченная дифференцируемая в ±∞ функция ![]() сходится к соответствующему ILN Ω (f) тогда и только тогда, когда
сходится к соответствующему ILN Ω (f) тогда и только тогда, когда ![]() .
.
Предельный переход в формуле Лагранжа, записанной для функции f:
![]() ,
,
составляет доказательство Теоремы 3.
Теорема 3 позволяет доказать, что последовательность {![]() }, определённая для всех
}, определённая для всех ![]() , например, формулой
, например, формулой ![]() , при
, при ![]() , сходится к соответствующему ILN
, сходится к соответствующему ILN ![]() .
.
Как известно, количество ![]() простых чисел p, p ≤ x, определяется асимптотической формулой
простых чисел p, p ≤ x, определяется асимптотической формулой ![]() . Так как функция g неограниченна и g´ (∞) = 0, то по Теореме 3
. Так как функция g неограниченна и g´ (∞) = 0, то по Теореме 3 ![]() . Следовательно, количество всех простых чисел равно некоторому ILN
. Следовательно, количество всех простых чисел равно некоторому ILN ![]() , что объясняет неограниченность последовательности
, что объясняет неограниченность последовательности ![]() , расстояний между последовательными простыми числами.
, расстояний между последовательными простыми числами.
Пусть для сходящегося числового ряда ![]() Следовательно, остаток rk ряда определяется равенством
Следовательно, остаток rk ряда определяется равенством ![]() . Тогда
. Тогда ![]() . Пара (k, m) переменных в последнем предельном равенстве является (Утверждение 5) C -точной парой натуральных переменных, то есть ∃ C, С > 0, такое что,
. Пара (k, m) переменных в последнем предельном равенстве является (Утверждение 5) C -точной парой натуральных переменных, то есть ∃ C, С > 0, такое что, ![]() Поэтому из
Поэтому из ![]() →0 следует [1, c. 105], что
→0 следует [1, c. 105], что
![]()
Доказана [1, c. 107] независимость сходимости числового знакопеременного ряда от перестановки его слагаемых, для чего, в частности, из понятия частичной суммы ряда ![]() и его остатка были выделены значения этих сумм (конечной и бесконечной, соответственно). Это утверждение иллюстрируется с помощью С-точной пары (1).
и его остатка были выделены значения этих сумм (конечной и бесконечной, соответственно). Это утверждение иллюстрируется с помощью С-точной пары (1).
СПИСОК ЛИТЕРАТУРЫ:
1. Cухотин А.М. Начало высшей математики: учеб. пособие . - 2-е изд., перераб. и доп. - Томск: Изд-во ТПУ, 2004. - 148 с.
Работа представлена на научную международную конференцию «Проблемы высшего и профессионального образования», 8-15 августа 2007 г., Коста Брава (Испания). Поступила в редакцию 05.06.2007.
Библиографическая ссылка
Сухотин А.М. С-ТОЧНЫЕ ПАРЫ НАТУРАЛЬНЫХ ПЕРЕМЕННЫХ И ИХ ПРИЛОЖЕНИЯ В АНАЛИЗЕ И В ТЕОРИИ ЧИСЕЛ // Современные наукоемкие технологии. 2007. № 12. С. 62-63;URL: https://top-technologies.ru/ru/article/view?id=25814 (дата обращения: 13.03.2026).



