C4H8 (CH3)2 → C4H8CH3C0H → C4H8 CH3C0OH → C4H8 COH C0OH → C3H6(COOH)3, (1)
где C4H8 (CH3)2 - параксилол, C4H8CH3C0H - паратолуиловый ангидрид, C4H8 CH3C0OH - паратолуиловая кислота , C4H8 COH C0OH - карбоксибензальдегид, C3H6(COOH)3 - терефталевая кислота. Предполагается, что будет использоваться двуярусная механическая мешалка. Для построения математической модели реактора построим физические модели микро - и макромасштабных процессов переноса. В дальнейшем процесс хемосорбции будем рассматривать в рамках модели турбулентного диффузионного пограничного слоя:
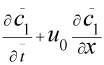 = D
= D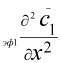 , (2)
, (2)
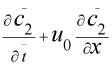 = Dэф2
= Dэф2 ![]() ,
,
где ![]() ,
, ![]() - средние концентрации веществ, переносимых вдоль химического реактора; u0 - скорость конвективного потока;
- средние концентрации веществ, переносимых вдоль химического реактора; u0 - скорость конвективного потока; ![]() , x - Эйлерова система координат; Dэф1 , Dэф2 - эффективные коэффициенты диффузии. Это система дифференциальных уравнений в частных производных с учетом химических реакций. Уравнения массопередачи , описывающие элементарный акт хемосорбции, принимались в соответствии с моделью:
, x - Эйлерова система координат; Dэф1 , Dэф2 - эффективные коэффициенты диффузии. Это система дифференциальных уравнений в частных производных с учетом химических реакций. Уравнения массопередачи , описывающие элементарный акт хемосорбции, принимались в соответствии с моделью:
![]() =
= 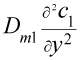 - k1
- k1 ![]() , (3)
, (3)
![]() =
= 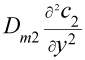 - k2
- k2 ![]() ,
,
где c1, c2 - концентрации п - ксилола и п - карбоксибензальдегида; ![]() - относительная скорость подъема пузыря; Dm1, Dm2 - коэффициенты молекулярной диффузии; k1 , k2 - кинетические константы соответствующих стадий процесса окисления; n1, n2 - порядки стадий. При этом предполагается, что лимитирующей стадией процесса является стадия расходования п - карбоксибензальдегида.
- относительная скорость подъема пузыря; Dm1, Dm2 - коэффициенты молекулярной диффузии; k1 , k2 - кинетические константы соответствующих стадий процесса окисления; n1, n2 - порядки стадий. При этом предполагается, что лимитирующей стадией процесса является стадия расходования п - карбоксибензальдегида.
Уравнения (3) использовались со следующими граничными условиями:
c1 = ![]() , c2 =
, c2 = ![]() │
│![]() , (4)
, (4)
c1 = 0, ![]() = 0 |
= 0 | ![]() ,
,
c2 = ![]() ,
, ![]() = 0 |
= 0 | ![]() ,
,
где t - время жизни пузыря, зависящее от частоты турбулентности на верхнем уровне иерархической системы. В дальнейшем уравнения (3) обезразмеривались в соответствии со следующими выражениями:
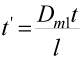 ;
; 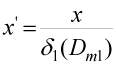 ;
; 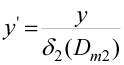 ; (5)
; (5)
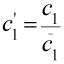 ;
; 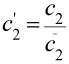 ;
;
где ![]() и
и ![]() - величины соответствующих диффузионно - реакционных пограничных слоев. Решение системы уравнений (3) с граничными условиями (4) позволяет определить молекулярные диффузионные потоки на поверхность дисперсионного включения ( пузыря ) в следующем виде:
- величины соответствующих диффузионно - реакционных пограничных слоев. Решение системы уравнений (3) с граничными условиями (4) позволяет определить молекулярные диффузионные потоки на поверхность дисперсионного включения ( пузыря ) в следующем виде:
![]() , (6)
, (6)
![]() .
.
Процессы в ядре потока сплошной фазы ректора могут описываться диффузионной моделью Данквертса для химических реакций, протекающих с существенно различными скоростями. Для решения уравнений (2) в случае прямотока газовой и жидкой фаз необходимо задать следующие граничные условия:
![]() =
= ![]() ,
, ![]() =
= ![]() |
| ![]() , (7)
, (7)
![]() = 0,
= 0, ![]() =
= ![]() ,
,
где L - длина реактора (12,5 м). Предполагая, что диффузионное сопротивление в межфазного переноса сосредоточено в ламинарном подслое, можно определить время пребывания реакционной смеси в реакторе ![]() 1 час. Система уравнений (1 -7) позволяет моделировать процессы переноса со сложными химическими реакциями в промышленных реакторах большой единичной мощности (150 тыс.т./год).
1 час. Система уравнений (1 -7) позволяет моделировать процессы переноса со сложными химическими реакциями в промышленных реакторах большой единичной мощности (150 тыс.т./год).
Библиографическая ссылка
Федоров А.Я., Мелентьева Т. А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЕАКТОРА ОКИСЛЕНИЯ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ // Современные наукоемкие технологии. 2007. № 11. С. 115-116;URL: https://top-technologies.ru/ru/article/view?id=25729 (дата обращения: 13.03.2026).



