Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Калмыков И.А. Кихтенко О.А. Барильская А.В.

Статья в формате PDF

143 KB

Процедура возведения символа (элемента) конечного поля GF(p) в степень трудоёмка и требует больших затрат на решение уравнения

α^x ≡ β(mod p),                  (1)

где α, β, x - элементы конечного поля Галуа с характеристикой p.

Для восстановления исходного значения α из получаемого значения β по модулю p используется уравнение:

.             (2)

Реализовать выражение (1) можно, используя умножитель по модулю p, однако время данной операции будет равно

T_оп = (х - 1) T_ум,

где T_ум - время выполнения модульного умножения.

Сократить время выполнения операции можно, используя индексы.

В работе [1] показана возможность использования теории индексов для эффективной реализации операций мультипликативного типа (умножение, деление, возведение в степень). Число i_A являющееся решением сравнения

,                    (3)

называется индексом числа A и обозначается . Первообразный корень g-основание индекса.

В работе [1] доказана теорема, по которой индекс J произведения простых целых чисел А₁ , А₂ ,..., А_k по модулю р равен сумме индексов сомножителей, взятой по модулю р-1, т.е.

,                     (4)

где i₁ ,i₂ ,..., i_k- индексы положительных чисел A₁ ,A₂ ,...,A_k по модулю р при первообразном коде g.

Т.о., очевидна возможность сведения операции умножения двух операндов А и В по модулю р к операции суммирования индексов i_A, i _B этих операндов при первообразном корне g по модулю р-1.

Аналогично можно доказать, что операцию возведения в степень (1) можно свести к операции индексов по модулю p-1.

Т.о., для нахождения индекса какого-либо числа A по модулю p надо найти первообразный корень числа p и решение сравнения (1) для данного первообразного корня. Эта операция сравнима по сложности с процедурой вычисления дискретного логарифма в конечном поле.

Аналогичная ситуация возникает и в расширенных полях Галуа . Т. к. все элементы этого поля получаются с помощью порождающего полинома р(z), то в качестве первообразного корня можно выбрать z. Тогда любой элемент A(z) поля  можно представить в виде

              (5)

Следовательно, справедливо

.                     (6)

При этом

            (7)

Т. к. значение показателя γ задано, то для реализации выражения (6) необходимо определить значение индекса i_A по модулю p(z) из выражения (5).

Рассмотрим расширенное поле Галуа GF(2³). В этом поле определен порождающий полином p(z)=z³+z+1, который задает следующие элементы поля (таблица 1).

Таблица 1

Видно, что показатели степеней элементов поля  крутятся по модулю 7 = 2^{3 -1}.

Из таблицы 1 видно, при векторном представлении элементов , соответствующих нулевому, 3-ему, 5-ому и 6-ому индексу, в нулевом разряде присутствует единица a₀ = 1, а в элементах поля с индексами 1, 2, 4 - в данном разряде записан нуль a₀ = 0.

Единица в 1-ом разряде a₁=1 векторного представления соответствует индексам - 1, 3, 4, 5, в противном случае, при a₁₌₀  индексам 0, 2, 6.

Единица во 2-ом разряде a₂=1 векторного представления соответствует индексам - 2, 4, 5, 6, в противном случае, при a₂=0 - индексам 0, 1, 3.

Используя логические функции, можно записать следующие соответствие, приведенные в таблице 2.

Следовательно, для реализации устройства вычисления индекса могут быть использованы базовые логические функции. Структура устройства для вычисления индекса элемента поля Галуа по модулю приведена на рисунке 1.

Таблица 2

Устройство состоит из регистра 1, предназначенного для хранения элементов поля Галуа GF(2³), представленного а двоичном коде, блока 2 элементов НЕ, блока 3, состоявшего из 7 трехвходовых элементов И, шифратора 4 и выхода устройства 5. Выходы регистра 1 подключены к входу соответствующего элемента НЕ, входящего в состав блока 2.

Входы 1-го элемента И блока 3 подключены к выходам 2-ого и 3-его элементов НЕ блока 2 и к 1-ому выходу регистра 1. Входы 2-ого элемента И блока 3 подключены к выходам 1-ого и 3-его элементов НЕ блока 2 и ко 2-ому выходу регистра 1. Входы 3 элемента И блока 3 подключены к выходам 1-ого и 2-ого элементов НЕ блока 2 и к 3-ему выходу регистра 1. Входы 4 элемента И блока 3 подключены к выходу 3-его элемента НЕ блока 2 и к 1-ому и 2-ому выходам регистра 1. Входы 5 элемента И блока 3 подключены к выходу 1-ого элемента НЕ блока 2 и ко 2-ому и 3-ему выходам регистра 1. Входы 6 элемента И блока 3 подключены к 1-ому, 2-ому и 3-ему выходам регистра 1. Входы 7 элемента И блока 3 подключены к выходу 2-ого элемента НЕ блока 2 и к 1-ому и 3-ему выходу регистра 1.

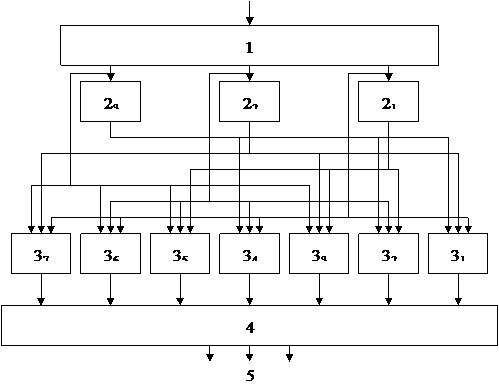
Рис. 1. Структура устройства

Выходы элементов И блока 3 подключены к входам шифратора 4, который преобразует семиразрядный унитарный код в двоичный трёхразрядный позиционный код. Выход шифратора 4 является выходом устройства 5.

СПИСОК ЛИТЕРАТУРЫ:

1. Акушский И.Я., Юдицкий Д.М. Машинная арифметика в остаточных классах. - М.: Сов. радио, 1968. - 440 с.

Библиографическая ссылка