Во многих задачах изменение одного гена не позволяет выйти решению из локального оптимума. Если принять во внимание, что в случае сходимости популяции в локальном оптимуме мутация остаётся единственным механизмом, способным вывести популяцию из него, то проблема становится весьма значимой. Альтернативой этому варианту является использование операторов мутации, затрагивающих несколько элементов или несколько строк сразу [6].
В ходе эксперимента был использовании простой ГА со следующими настройками: количество хромосом - 50, разрядность гена - 16 бит, вероятность кроссовера - 90%, вероятность инверсии - 5%. В качестве тестовой функции использовали функцию De Jong5:
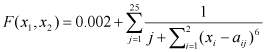 .
.
Оптимумом данной тестовой функции является максимум - 1,002. Был реализован модифицированный многострочный оператор мутации, работающий несколько иначе. В случае его использования вероятность мутации трактуется как вероятность мутации каждой хромосомы, а не единичной произвольно выбранной. В этом случае мутация может затронуть сразу несколько хромосом. Вероятность мутации менялась в интервале [0;0,12] с шагом 0,02. Результаты сведены в таблицу.
|
№ эксперимента |
Вероятность мутации |
Среднее количество поколений |
Оптимум |
|
1 |
0 |
80 |
0,359 |
|
2 |
0,02 |
156 |
0,521 |
|
3 |
0,04 |
196 |
0,532 |
|
4 |
0,06 |
150 |
0,881 |
|
5 |
0,08 |
97 |
0,941 |
|
6 |
0,1 |
104 |
0,762 |
|
7 |
0,12 |
74 |
0,682 |
Проведенный эксперимент показал, что эффективность работы однострочного оператора мутации при высокой вероятности самой мутации сравнима с эффективностью работы многострочного оператора мутации при традиционно низких вероятностях мутации порядка 0.06-0.8. Кроме того, высокие значения вероятности мутации в сочетании с многострочным оператором мутации наоборот сильно снижают эффективность работы алгоритма. Очевидно, что мутация оказывает значительное влияние на сходимость ГА. Следовательно, имеет смысл проводить ее дальнейшую модификацию, направленную на увеличение скорости сходимости ГА.
СПИСОК ЛИТЕРАТУРЫ:
- Курейчик В.М., Лебедев Б.К. Определения и основные понятия генетических алгоритмов. Интернет-лекция в рамках научной школы Третьей конференции молодых ученых.
- Цой Ю.Р., Спицин В.Г. Эволюционный подход к настройке и обучению искусственных нейронных сетей. Томский технический университет, Томск.
- Зайцева Е.Н., Станкевич Ю.А. Некоторые современные методы решения оптимизационных задач. Белорусский государственный университет информатики и радиоэлектроники, г. Минск.
- Емельянов В.В., Курейчик В.В., Курейчик В.М. Теория и практика эволюционного моделирования. М.: ФИЗМАТЛИТ, 2003.
- Снитюк В.Е.. Аспекты эволюционного моделирования в задачах оптимизиции. Киевский национальный университет им. Тараса Шевченко, г. Киев.
- Ершов А.Я., Сургутанов В.В. Моделирование, анализ сходимости и оптимизация мутаций простого генетического алгоритма. Инновационные технологии в обучении и производстве: Материалы III Всероссийская конференция, г. Камышин, 20-22 апреля 2005г.: В 3 т - Волгоград, 2005. Том 2 - 231 с.
Библиографическая ссылка
Чипига А.Ф., Колков Д.А., Конюшков В.А. ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВЕРОЯТНОСТИ ВОЗНИКНОВЕНИЯ ОПЕРАТОРА МУТАЦИИ НА СХОДИМОСТЬ ГЕНЕТИЧЕСКОГО АЛГОРИТМА // Современные наукоемкие технологии. 2007. № 10. С. 89-90;URL: https://top-technologies.ru/ru/article/view?id=25562 (дата обращения: 07.03.2026).



