Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Резеньков Д.Н.

Статья в формате PDF

135 KB

Сохранение работоспособного состояния вычислительного устройства ЦОС во многом определяется быстротой и точностью определения местоположения и глубины ошибки. При этом предпочтение отдается информационной, а не технологической надежности системы, которая может быть достигнута путем специального кодирования, обеспечивающего обнаружение ошибок, возникающих в результате сбоев, отказов элементов системы, и их исправление.

Одним из способов построения процедур поиска и локализации ошибок в модулярных кодах является методы и алгоритмы контроля и коррекции ошибок непозиционного кода ПСКВ, базирующиеся на вычисление позиционных характеристик во временной области [3].

В основу большинства алгоритмов поиска и коррекции ошибок в модулярных кодах положена процедура вычисления позиционной характеристики [1,2,4]. Реализация данного подхода предполагает использование некоторого функционально отношения, однозначно отражающего множество значений модульных характеристик в множество рассматриваемых ошибок Е. При этом необходимо, чтобы математическая модель, отражающая данное отношение, при реализации в нейробазисе обеспечивала бы параллельно-конвейерную организации вычислений.

Наличие одного избыточного основания в процедурах поиска и локализации ошибок модулярных кодов ПСКВ является недостаточным, так как корректирующие способности такого кода не позволяют исправить однократные ошибки по всем основаниям ПСКВ.

Для решения данной проблемы можно провести логическое упрочнение контрольного основания. Однако упрочнение контрольного основания требует значительного расширения диапазона обрабатываемых данных, поскольку специальным представлением вводится погрешность.

Альтернативным путем решения данной проблемы является метод определения правильности А(z)=a₁(z),...a₂(z),...a_k+1(z),...a_k+r(z)) на основе нулевизации, заключающейся в переходе от исходного полинома к полиному (0,0,...,γ_k+1(z),..., γ_k+r(z)), помощи преобразований, при которых не имеет место ни один выход за пределю рабочего диапазона системы.

Нулевизация заключается в последовательном вычитании из исходного полинома, представленного в модулярном коде, некоторых минимальных полиномов - констант нулевизации таких [1], что полином А(z) последовательно преобразуется в полином вида , затем в полином , и так далее. Продолжая данный процесс в течении k итераций, получается (0,0,...,γ_k+1(z),..., γ_k+r(z)).

Применение метода нулевизации позволяет последовательно получать наименьший полином, кратный сначала p₁(z), затем полином - кратный p₁(z) p₂(z), и в конечном итоге - кратный рабочему

.

Основным недостатком метода нулевизации [1] является последовательный характер вычислительного процесса, что и позволяет реализовать его на основе двухслойной нейронной сети. Это обусловлено тем, что константы нулевизации представляют собой наименьшие возможные числа

    (1)

где .

Решить данную проблему можно за счет отказа от констант нулевизации M_i(z) и перехода к использованию псевдоортоганальных полиномов. Если положить условие, что  где , то А(z)=a₁(z),a₂(z),...a_k(z)).

Тогда, согласно китайской теоремы об остатках, полином А(z) можно представить в виде

А(z)=(a₁(z),0,0,...,0)+(0, a₂(z),0,...,0)+(0,0,0,..., a_k(z)).                                             (2)

Каждое слагаемое выражения (2) представляет собой

(0,0,...,0, a_i(z),0,...,0)=           (3)

где - ортогональный базис, безизбыточной системы оснований.

Проведя расширение системы оснований p₁(z), p₂(z),..., p_k(z) на r контрольных p_k+1(z), p_k+2(z),..., p_k+r(z), представим  в виде

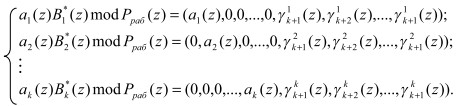   (4)

Подставим выражение (4) в равенство (2).

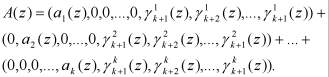                (5)

Следовательно,

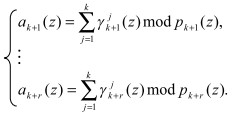  (6)

Значит, разность полинома А(z) псевдоортогональных форм, полученых согласно (4), задает величину нормированного следа полинома

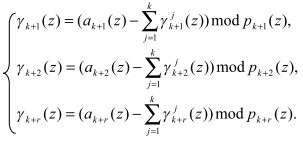 (7)

РассмотренныйПредставленный метод вычисления позиционной характеристики характеризуется довольно высокой надежностью работы при сравнительно малых затратах на реализацию процедур поиска и определения местонахождения ошибочных разрядов.

СПИСОК ЛИТЕРАТУРЫ:

1. Акушский И.Я., Юдицкий Д.М. Машинная арифметика в остаточных классах.-М.: Сов.радио, 1968. - 440 с.
2. Акушский И.Я., Бурцев В.М. Вычисление позиционной характеристики (ядро) непозиционного кода //Теория кодирования и оптимизации сложных систем. Алма-Ата:Наука, 1977. С.17-25.
3. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. нейросетевая реализация в ПСКВ операций ЦОС пвышенной разрядности/Нейрокомпьютеры: разработка и применение. №5-6, 2004, с. 94-101.
4. Червяков Н.И., Сахнюк П.А., Шапошников А.В., Ряднов С.А. Модулярные параллельные вычислительные структуры нейропроцессорных систем. - М.: ФИЗМАТЛИТ, 2003. - 288 с.
5. Долгов А.М. Диагностика устройств, функционирующих в системе остаточных классов. - М.: Радио и связь, 1982. - 64 с.

Библиографическая ссылка