Одним из способов охлаждения агломерата является его охлаждение на прямолинейном охладителе. Агломерат после агломерационной машины дробится, отсеивается от мелочи (<5-6 мм) и загружается с помощью устройства 1 (рис. 1) в короба, расположенные на бесконечном полотне охладителя. Охлаждение агломерата производится путем подачи воздуха с помощью дутьевых камер расположенных под коробами (рис. 1).
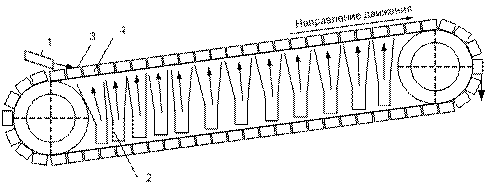
Рис. 1. Схема прямолинейного охладителя: 1 - загрузочное устройство; 2 - дутьевые камеры; 3 - короб;.4 - агломерат.
Одной из проблем производства агломерата являются большие потери энергии при охлаждении агломерата на прямолинейном охладителе. Для разработки предложений по сокращению потерь необходимо исследование процесса охлаждения агломерата. Для этого используют метод математического моделирования.
В известной математической модели [1] процесса охлаждения агломерата представлен только теплообмен между материалом и газом. В ней не учитывается влияние газодинамических процессов на теплообмен в слое.
В данной работе разработана математическая модель охлаждении агломерата, которая включает подмодель конвективного теплообмена и подмодель газодинамики.
На рис. 2 приведена схема расчетной области для моделирования теплообмена в слое.
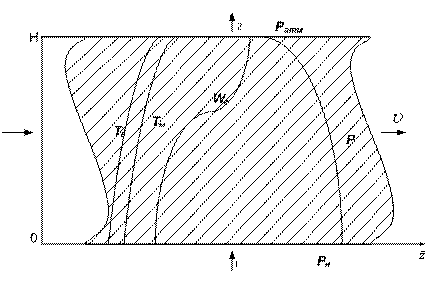
Рис. 2. Схема расчетной области: Tм(x, t), Tг(x, t), P(x,t),Wг(x,t) - типичные распределения температуры агломерата, газа, давления и вертикальной скорости движения газа по толщине слоя агломерата; Н - высота слоя, Ратм и Рк - атмосферное давление и давление в камере
Подмодель теплообмена в однородном по фракционному составу слое включает:
- уравнение баланса тепла газов:
и граничные условия: tz= tz0 при y=0;
- уравнение баланса тепла агломерата:
и начальные условия: tm = tm0 при t=0;.
В уравнениях (1) - (2) приняты обозначения: tг и tм -
температуры газа-теплоносителя и материала; t - время, с; у
- координата по глубине слоя, м; сm -теплоемкость материала, Дж/(К∙кг); Wг - скорость
газа на свободное сечение, м3/(м2с); ρм - кажущаяся плотность материала,
кг/м3; ρг
-плотность газа, кг/м3; m - порозность слоя; αV - объемный коэффициент теплоотдачи, ![]() .
.
Объемный коэффициент теплоотдачи αV определяется по формуле [2]:
где d - диаметр куска агломерата, м; M´ = 1,0 для идеальных условий, M´ = 0,5 при наличии мелочи 20% (M´ зависит в основном от равномерности распределения газов по поперечному сечению слоя).
Подмодель газодинамики включает:
- уравнение движения газа в слое дисперсного материала:
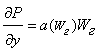 ; (3)
; (3)
- уравнение неразрывности газового потока:
где
Плотность газа и давление связаны зависимостью:
![]() , (5)
, (5)
где ![]() ; ρ0, Р0 и Т0
- плотность газа, давление и температура при нормальных условиях.
; ρ0, Р0 и Т0
- плотность газа, давление и температура при нормальных условиях.
Из уравнений (3) и (4) получено уравнение для определения давления в каждой точке по высоте слоя дисперсного материала:
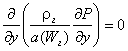 , (6)
, (6)
при
граничных условиях при у = 0: Р = Рн; при
у = H: Р = Ратм. (7)
где
Рн = Рк - ΔРкр; Pк - давление в камере, Па; ![]() - сопротивление колосниковой решетки, Па, ρгк -плотность газа на выходе
из слоя при нормальных условиях, кг/м3; Wгк - скорость газа на выходе из слоя при нормальных
условиях, м/с; xк - коэффициент сопротивления колосниковой решетки.
- сопротивление колосниковой решетки, Па, ρгк -плотность газа на выходе
из слоя при нормальных условиях, кг/м3; Wгк - скорость газа на выходе из слоя при нормальных
условиях, м/с; xк - коэффициент сопротивления колосниковой решетки.
После расчета давления в каждой точке слоя определяется скорость газа по формуле, полученной из уравнения (3):
Уравнения (1), (2) и (6) решаются для сечения
Представленное выше математическое описание процессов тепловых и газодинамических процессов при охлаждении агломерата приведено к дискретному виду с помощью численного метода Рунге-Кутта. Разработана компьютерная модель с использованием алгоритмического языка Turbo Pascal 7.0.
Тестирование алгоритма расчета процессов конвективного теплообмена в неподвижном плотном слое проведено путем сравнения результатов моделирования с решением задачи Шумана, полученным В.Н. Тимофеевым в интегральной форме. Интегрирование выполнено с помощью математического пакета MathCad. В результате тестирования установлено, что для того, чтобы относительная погрешность определения температуры не превышала 1 %, необходимо выбирать количество узлов в расчетной области не менее 65 для высоты слоя 200 мм.
Проведена проверка адекватности модели тепловых и газодинамических процессов при охлаждении агломерата путем сравнения результатов моделирования с экспериментальными данными по температуре на отметке соответствующей 45 м от начала прямолинейного охладителя для различных скоростей движения полотна. Экспериментальные данные, представленные на рис. 3, получены при проведении исследований ЧерМК ОАО «Северсталь».
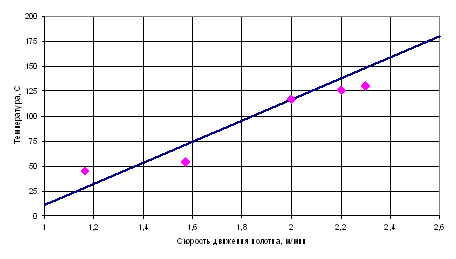
Рис. 3. Зависимость температуры отходящего газа на отметке 45 м от скорости движения полотна: *- экспериментальные данные; ‑ - моделирование.
Как следует из рис. 3, результаты моделирования удовлетворительно согласуются с экспериментальными данными.Таким образом, в настоящей работе представлена математическая модель тепловых и газодинамических процессов при охлаждении агломерата. Модель отличается от известных учетом газодинамических процессов, происходящих в слое агломерата. Модель планируется использовать:
- для исследования закономерностей охлаждения агломерата на прямолинейном охладителе;
- при обосновании различных способов совершенствования технологии охлаждении агломерата;
- при разработке системы управления процессом охлаждении агломерата на прямолинейном охладителе.
СПИСОК ЛИТЕРАТУРЫ:
1. Н.М. Бабушкин, С.Г. Братчиков, Г.Н. Намятов, В.С. Швыдкий, Ф.Р. Шкляр, Ю.Г. Ярошенко // Охлаждение агломерата и окатышей. - М.:Металлургия, 1975 г. 208с.
2. Б.И. Китаев, Б.Ф. Зобнин, В.Ф. Ратников, А.С. Телегин, В.Г. Лисиенко, С.Г. Братчиков, М.Д. Казяев, В.П. Маркин, Е.Л. Суханов, В.Д. Сучков // Теплообмен в доменной печи. Изд-во «Металлургия», 1966 г.
Библиографическая ссылка
Кабаков З.К., Елисеев А.А., Веселов Ю.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕПЛОВЫХ И ГАЗОДИНАМИЧЕСКИХ ПРОЦЕССОВ ПРИ ОХЛАЖДЕНИИ АГЛОМЕРАТА // Современные наукоемкие технологии. 2009. № 8. С. 27-30;URL: https://top-technologies.ru/ru/article/view?id=25537 (дата обращения: 01.03.2026).



