Успехи, достигнутые в области технологии изготовления наноматериалов и тонкопленочных наноструктур за последнее время, привлекают пристальное внимание исследователей к изучению различных свойств наноструктур. Тонкие пленки высокотемпературных сверхпроводников демонстрируют свойства, которые не могут проявиться в объемном сверхпроводнике. Возможность эффективного взаимодействия электромагнитной волны с решеткой вихрей Абрикосова в тонких пленках сверхпроводника второго рода показана в работах [1, 2].
Рассмотрим тонкую
пленку сверхпроводника второго рода, находящегося на подложке из полупроводникового
материала. Толщина слоя сверхпроводника t, причем t <<λ, где λ-лондоновская глубина проникновения магнитного поля в
сверхпроводник. Направим ось Oy перпендикулярно границам раздела слоев, ось Ox
параллельно границам раздела. Вся структура находится в магнитном поле By0, направленном противоположно оси Oy. Величина магнитного
поля находится в диапазоне
, где Bc1 - значение первого
критического поля для сверхпроводника, Bc2 второе критическое
поле. Под действием транспортного тока, направленного перпендикулярно полю By0 вдоль оси Oz, решетка
вихрей Абрикосова в слоях сверхпроводника приходит в движение вдоль оси Ox. Рассмотрим
распространение в данной структуре Н-волны в плоскости xOy под углом θ к оси Oy. Для простоты
будем предполагать, что в плоскости слоев поля зависят только от одной
координаты, и положим
=0. Как показано в работах [1, 2], наличие тонкой
сверхпроводящей пленки можно учесть введением специального граничного условия
, (1)
где 
- плотность
транспортного тока в сверхпроводнике, η - коэффициент вязкости
магнитного вихря, t - толщина сверхпроводящей
пленки,By0 - величина внешнего магнитного
поля, Ф0 - квант магнитного
потока. Пусть волна из полубезграничного диэлектрика падает на тонкий слой
сверхпроводника под углом q 1 и выходит
в слой полупроводника под углом q 2. Коэффициент
отражения от структуры сверхпроводник - полупроводник имеет вид
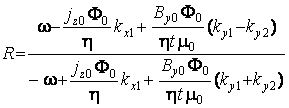, (2)
где 
, 
, ε1,2 и μ1,2 - диэлектрическая и
магнитная проницаемость сред, индексы 1 и 2 относятся к диэлектрику (воздуху в
рассматриваемом случае) и полупроводнику.
В качестве полупроводника рассмотрим полярный полупроводник (например, GaAs или AlGaAs). В рамках модели диэлектрического континуума диэлектрическая проницаемость полупроводника определяется выражением 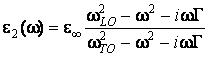[3]
, (3)
где, 
- решеточная часть
диэлектрической проницаемости,ωL,O и ωT,O - частоты продольного
и поперечного фононов, Г - столкновительная
частота.
На рисунке 1 а, б представлены результаты численного расчета коэффициента отражения от структуры сверхпроводник - полупроводник в зависимости от величины угла падения для разных значений величины внешнего магнитного поля By0.
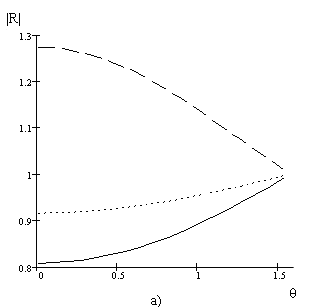
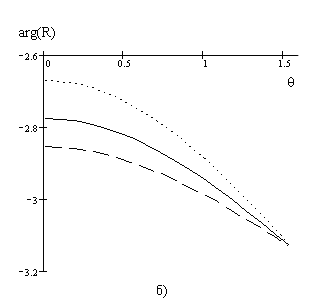
Рис. 1, а), б). Зависимость модуля (а) и фазы (б) коэффициента отражения от угла
падения. Сплошная линия: 
, короткий пунктир: 
, длинный пунктир: 
. Параметры структуры 
, 
, 
.
Таким образом, рассмотренная в работе структура, содержащая тонкий слой сверхпроводника второго рода и слой полупроводника, может применяться при создании различного рода устройств, например усилителей или фильтров, параметры которых зависят от частоты падающей электромагнитной волны и от величины внешнего магнитного поля. Управление полосой пропускания - усиления в таких устройствах может осуществляться путем изменения внешнего магнитного поля.
СПИСОК ЛИТЕРАТУРЫ
1. Глущенко А.Г., Головкина М.В. // Письма в ЖТФ. -1998. - Т. 24. - Вып. 1. -С. 9.
2. Попков А.Ф. // Письма в ЖТФ. - 1989. - Т. 15. -Вып. 5. - С. 9.
3. Ю П., Кардона М. Основы физики полупроводников. - М.: Физматлит. -2002. - 560 с.
4. Glushchenko A.G., Golovkina M.V. // International Symposium on Electromagnetic Compatibility "EMC´98 ROMA" Rome, Italy. -1998. -V 2. -P. 483.
Библиографическая ссылка
Головкина М.В. ОТРАЖЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ОТ СИСТЕМЫ СВЕРХПРОВОДНИК-ПОЛУПРОВОДНИК // Современные наукоемкие технологии. 2009. № 8. С. 8-10;URL: https://top-technologies.ru/ru/article/view?id=25530 (дата обращения: 20.05.2025).