Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

П.Г. Яковенко

Статья в формате PDF

149 KB

Моделирование переходных процессов в инерционных системах набором обыкновенных дифференциальных уравнений не вызывает затруднений. Оно дает возможность воспроизводить  с высокой точностью переходные процессы с учетом специфики функционирования системы при различных управляющих воздействиях, контролировать изменение координат, учитывать изменение заданий, параметров и ограничений. Для совершенствования алгоритмического обеспечения микропроцессорных систем управления переходными процессами следует использовать новые средства прикладной математики.

Предложена методика последовательного многошагового синтеза оптимальных по быстродействию управлений линейными и нелинейными системами с ограничением координат, основанная на многократном численном решении обыкновенных дифференциальных уравнений. Оптимальный закон составляется из управлений, найденных во время переходного процесса для малых интервалов времени. Поиск управлений ведется последовательно по шагам с учетом нелинейностей, ограничений и координат системы, полученных при оптимальном управлении  на предыдущих шагах. Методика предполагает использование методов динамического программирования и имитационного моделирования, принципов «перемены цели» и «ведущего слабого звена». На модели выполняется целенаправленный поиск оптимального управления для очередного шага с  учетом прогноза будущего состояния системы.

Рассмотрим пример синтеза оптимального по быстродействию управления инерционной системой, состоящей из двух последовательно включенных элементов, в которой во время переходного процесса возможно изменение заданий, ограничений и параметров.

Управляющее воздействие U действует на вход первого элемента, описываемого дифференциальным уравнением

,

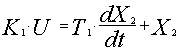где K₁ и T₁ - коэффициент передачи и постоянная времени первого элемента; X₂ - выходная координата первого элемента; t  - время.

Выходная координата первого элемента является входной координатой для второго элемента, описываемого дифференциальным уравнением

,

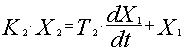где K₂ и T₂ - коэффициент передачи и постоянная времени второго элемента; X₁ - выходная координата второго элемента.

Максимальные значения управляющего воздействия U и выходной координаты первого элемента X₂ не должны превышать соответственно значений U_M и X_2M. Эти ограничения, задание по координате X_z1, параметры инерционной системы K₁ и T₁, K₂ и T₂ могут изменяться в момент времени T_З в течение переходного процесса.

Определим оптимальное управление U(t), обеспечивающее минимальное время перевода системы из исходного состояния с реальными координатами X1i и  X2i в заданное состояние с координатами X₁ = X_z1 и X₂ = X_z1 / K₂  с учетом ограничений U_M и X_2M. Решение задачи с помощью предложенной методики предполагает, что речь идет о системе с квантованием координат по уровню и по времени. При этом  инерционная система описывается разностными уравнениями

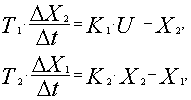
где ΔX₁ и ΔX₂ -  приращения координат системы за шаг интегрирования Δt. Управление U(t) инерционной системой вычисляется по шагам в виде значений U₀, ,...,U_c .

Синтез закона управления начинается с расчета времени

T = T + Δt

на очередном шаге и сравнении его с T_З. Ограничения U_M и X_2M, задание по координате X₁, параметры инерционной системы K₁ и T₁, K₂ и T₂ могут принимать новые значения когда T превысит T_З.

Определение управления на очередном шаге предполагает расчет требуемого приращения выходной координаты второго элемента

.

По разностному уравнению определяется значение выходной координаты первого элемента X_2p1, способное обеспечить такое приращение ΔX_1p1

.

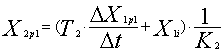Полученное значение выходной координаты первого элемента X_2p1 при необходимости ограничивается значением X_2M с соответствующим знаком. Затем вычисляется требуемое приращение выходной координаты первого элемента ΔX_2p1 на шаге

.

По разностному уравнению определяется управление на первом пробном шаге U_p1, способное обеспечить такое приращение ΔX_2p1 на шаге

.

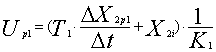Полученное значение управления Up1 при необходимости ограничивается значением UM с соответствующим знаком. Чтобы обеспечить соблюдение ограничения по координате X₁ выполняется расчет первого пробного шага. Последовательно вычисляются с найденным управлением U_p1 новые приращение выходной координаты первого элемента ΔX_2p1, значение выходной координаты первого элемента X_2p1, приращение выходной координаты второго элемента ΔX_1p1 и значение выходной координаты второго элемента X_1p1

,

,

,

.

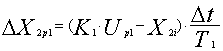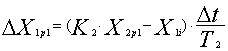Полученные значения координат позволяют задать начальные условия для второго пробного шага при переводе системы в равновесное состояние

,

.

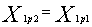Расчет управления для второго пробного шага начинается с определения по разностному уравнению требуемого приращения выходной координаты первого элемента ΔX_2p2

.

Если модуль суммы значений X_2p2 и ΔX_2p2 не превышает X_2M, то значение ΔX_2p2 остается неизменным. В противном случае определяется величина ΔΔ превышения этой суммой значения X_2M

.

Если сумма значений X_2p2 и ΔX_2p2 окажется больше нуля, то значение ΔX_2p2 определяется по выражению

.

В противном случае значение ΔX_2p2 определяется по выражению

.

По разностному уравнению определяется управление U_p2 на втором пробном шаге, способное обеспечить такое приращение ΔX_2p2 на шаге

.

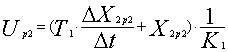Полученное значение управления U_p2 при необходимости ограничивается значением U_M с соответствующим знаком. С найденным управлением U_p2 выполняется расчет второго пробного шага. Последовательно вычисляются  новое приращение выходной координаты первого элемента ΔX_2p2, значение выходной координаты первого элемента X_2p2, приращение выходной координаты второго элемента ΔX_1p2 и значение выходной координаты второго элемента X_1p2 

,

,

,

.

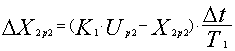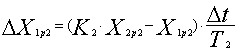Проводится проверка, находится система в равновесном состоянии или нет. Для этого оценивается значение ΔX_1p2. Если модуль ΔX_1p2 окажется больше нуля, то выполняется расчет по ранее описанной методике следующего второго пробного шага. Расчеты вторых пробных шагов по такому циклу каждый раз с новыми начальными условиями, полученными в результате выполнения предыдущего второго пробного шага, продолжаются до тех пор, пока модуль ΔX_1p2 не станет равным нулю и система не будет переведена в равновесное состояние.

После этого контролируется выполнение ограничения по координате X1. Если значение X1p2 превышает значение Xz1, то найденное на первом пробном шаге управление Up1 не является оптимальным для очередного шага. Следует вычислить приращение ΔX₂ по координате X2 за шаг, исходя из условия нахождения системы в состоянии равновесия, и определить обеспечивающее его управление U, которое при необходимости ограничивается значением UM с соответствующим знаком

,

.

Управление U считается оптимальным и используется в дальнейшем в качестве управляющего воздействия U_i при расчете реальных координат системы X_1i и  X_2i на шаге.

Если после контроля выполнения ограничения по выходной координате X₁ значение X_1p2 не превышает значение X_z1, то ранее найденное на первом пробном шаге управление U_p1 считается оптимальным для очередного шага и используется в дальнейшем в качестве управляющего воздействия U_i при расчете реальных координат системы X_1i и  X_2i на очередном шаге.

Выполняется расчет координат системы после выполнения реального шага. Последовательно вычисляются по разностным уравнениям от входа к выходу системы с найденным управлением U_i новое приращение выходной координаты первого элемента ΔX_2i, значение выходной координаты первого элемента X_2i, приращение выходной координаты второго элемента ΔX_1i, значение выходной координаты второго элемента X_1i

,

,

,

.

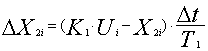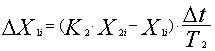Затем происходит возврат в начало алгоритма для расчета оптимального управления на следующем шаге с начальными условиями, полученными в результате выполнения предыдущего реального шага. Таким способом последовательно составляется оптимальный по быстродействию закон с учетом принятых ограничений из управлений U_i, найденных во время переходного процесса для малых интервалов времени.

Испытания алгоритма показали его высокую эффективность при изменениях во время переходного процесса задания X_z1, ограничений  U_M и X_2M, параметров системы K₁ и T₁, K₂ и T₂. Во всех случаях синтезировался закон управления инерционной системой при строгом выполнении принятых ограничений. Нарушение ограничений по предложенному алгоритму возможно только в случае, если для выполнения нового задания во время переходного процесса не хватает динамических возможностей системы.

Разработанный алгоритм позволяет оптимизировать управление переходными процессами при наличии математического описания системы в виде обыкновенных дифференциальных уравнений. Возможен синтез микропроцессорными средствами в реальном масштабе времени оптимальных управлений и нелинейными системами с ограничениями координат.

Библиографическая ссылка