Из сказанного выше следует, что сила, с которой источник магнитного поля действует на парамагнетик или наоборот сила, с которой парамагнетик действует на источник магнитного поля, определяется квадратом индукции магнитного поля. Это действительно так, поскольку намагниченность вещества J (магнитный момент единицы объема) пропорциональна индукции магнитного поля, сила же, с которой неоднородное магнитное поле действует на магнитный момент, определяется изменением того же магнитного поля с координатой. Если теперь магнитное поле создается не одним магнитным моментом, а несколькими, то появляющиеся после возведения в квадрат двух или более слагаемых перекрестные слагаемые не обязаны обнулиться даже при усреднении по всему пространству, занимаемому магнетиком. В любом случае, это должно быть проверено.
Пусть ориентация двух источников магнитного поля (магнитных моментов m1 и m2) относительно неподвижной системы координат XYZ задана соотношениями
, (1)
, (2)
а положение магнитного момента m2 в пространстве задано вектором:
. (3)
То есть предполагается, что оба магнитных момента находятся в одной плоскости XOY, положение же магнитного момента m2 задано смещенной вдоль оси Y на расстояние y0 полярной системой координат с азимутальным углом φ и радиус-вектором R; φ+α - угол между магнитным моментом m2 и осью OX. Положение точки поля определяется вектором
(4)
с компонентами
,(5)
,(6)
, (7)
s,ψ,υ - координаты сферической системы координат, связанной с магнитным моментом m2 (рис. 1). Одной из целей настоящей работы является изучение распределения поля в окрестностях магнитного момента m2. В этих переменных индукции магнитного поля, создаваемого в точке с радиус-вектором r магнитными моментами m1 и m2, соответственно, равны
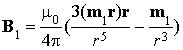, (8)
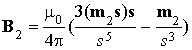(9)
и их компоненты
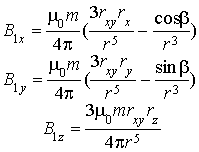, (10)
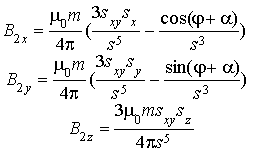, (11)
где
, (12)
, (13)
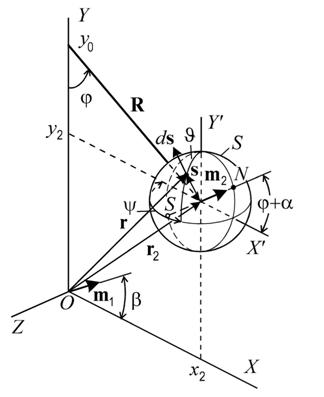
Рис. 1. Геометрия расчета магнитного поля, создаваемого двумя магнитными моментами m1 и m2.
. (14)
Первое, что представляет несомненный интерес, это распределение индукции магнитного поля вблизи магнитного момента m2, способного совершать вращательное движение вокруг точки, расположенной на оси Y на расстоянии y0 от начала системы координат XYZ. Имеет смысл рассмотреть две симметрично расположенные относительно магнитного момента m2 точки N и S, для которых
,
.
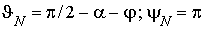Расчет индукции магнитного поля
(15)
чрезвычайно прост, тем не менее, обнаруживает достаточно перспективный результат. Зависимость модуля индукции магнитного поля BN в точке N перед магнитным моментом от угла поворота φ существенно отличается от такой же величины BS позади него (рис. 2). Но самое важное в другом. Разница между величинами индукций магнитного поля исчезает при малых расстояниях от магнитного момента m2. Вообще говоря, это означает, что суперпозиция источников магнитного поля с практически нулевыми размерами ни к каким неожиданным эффектам, в том числе и вращению, не приводит.
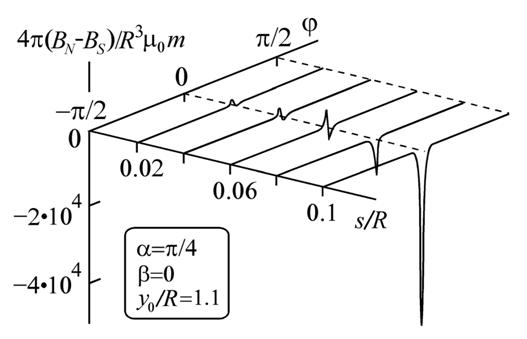
Рис. 2. Асимметрия магнитного поля вблизи полюсов магнитного момента m2.
Асимметрия магнитного поля еще мало, что означает. Важным является расчет сил, с которыми тот и другой магнитные моменты действуют на парамагнитную среду. Соответствующее выражение для плотности силы можно переписать не задумываясь [4]. Однако, в дальнейшем обязательно возникнет вопрос о сохранении энергии для такой системы. Поэтому безопаснее при рассмотрении сил исходить из энергии, которой обладает магнетик в магнитном поле.
В свободном пространстве магнитное поле, индукция которого B0=μ0H, обладает энергией
. (16)
В пространстве, заполненном однородным магнетиком с относительной магнитной проницаемостью m напряженность магнитного поля не изменяется, но B=μ0μH, поэтому при наличии магнетика энергия поля становится равной:
. (17)
Это означает, что при заполнении всего пространства магнетиком энергия поля увеличивается. Другими словами, внося намагниченное тело в магнитную среду или намагничивая тело в магнитной среде, совершается работа, отличающаяся от работы, которая затрачивается на намагничивание в свободном пространстве. Теперь можно считать, что энергией магнетика во внешнем магнитном поле является величина
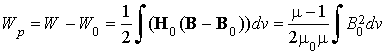, (18)
что со ссылкой на закон сохранения энергии позволяет записать полную силу, действующую на магнетик:
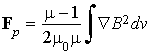. (19)
На самом деле нас больше всего интересует не эта сила, а лишь та ее часть, которая создается магнитным моментом m2; это слагаемое полной силы, взятое с обратным знаком, представляет собой силу, с которой парамагнетик действует на магнитный момент m2 и, возможно, вызывает его вращение. Представим
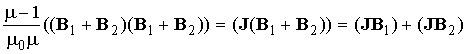. (20)
Слагаемое (JB1) ответственно за силу, с которой первый магнитный момент действует на парамагнетик, такая же величина силы действует то тот же магнитный момент m1, на состояние второго магнитного момента это слагаемое не влияет. Поэтому интерес представляет собой только сила
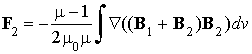, (21)
с которой среда действует на способный перемещаться магнитный момент m2. При этом интеграл от градиента B22 по всей бесконечной области, разумеется, равен нулю. Более того, определенное значение имеет не полная сила, направление которой не определено, а ее проекция F2t , скажем, на направление касательной к окружности радиуса R.
При вычислении интеграла (21) необходимо интегрирование провести, вообще говоря, по всему бесконечному объему, занимаемому парамагнетиком. Если источники магнитного поля точечные этот интеграл равен нулю. Будем считать, что магнитные моменты, или, по крайней мере, один из них - m2, находятся внутри сфер, вещество внутри которых механически не взаимодействует с внешней средой. В такой модели интегрирование в (21) следует провести по всему пространству за исключением объемов, занимаемых сферами. В свою очередь это означает, что сила, с которой среда действует на находящийся внутри сферы магнитный момент m2, отличается от (21) только знаком, если область, которую занимает первый магнитный момент, мала. Такой подход позволяет заменить интегрирование по объему интегрированием по поверхности:
,
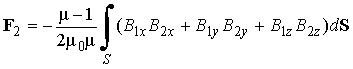где
,
,
поскольку элемент поверхности dS и вектор s коллинеарны (рис. 1). Результаты численного интегрирования, выполненного для различных радиусов s сферы, внутри которой находится способный вращаться магнитный момент, и для различных углов φ, показаны на рис. 3. То, что усредненное по всем углам j значение силы F2t практически равно нулю, не означает невозможность вращательного движения. В реальных технических устройствах любое движение, в том числе и вращательное, происходит при наличии трения или сопротивления среды. Асимметрия силы F2τ относительного нулевого значения делает вращательное движение возможным. Пример, демонстрирующий такой процесс, продемонстрирован на том же рисунке: движение становится возможным, если модуль силы F2τ превышает значение силы трения покоя Ff . Если же значение силы меньше модуля силы трения, магнитный момент m2 должен оставаться в состоянии покоя. Таким образом, трение выполняет роль храпового колеса. Но для того, чтобы храповое колесо привести в движение, нужно, чтобы оно от чего-то отталкивалось; роль этого «чего-то» выполняет парамагнитная среда. Получается, что взаимодействие суперпозиции магнитных моментов с парамагнитной средой действительно может привести к движению одного магнитного момента относительно среды и другого магнитного момента. Плохо то, что при этом существуют локальные положения устойчивости, в ряде случаев непозволяющее магнитному моменту m2 прийти в состояние движения из состояния покоя.
При намагниченности цилиндрических магнитов высотой 1 см радиусом 1 см, равной 107 А/м, значении R=3 см максимальное значение силы F2 составляет величину порядка 0.1 Н. Если же парамагнитной средой является такое необычное вещество, как жидкий кислород, для которого значение μ-1 в 2×105 раз больше, чем для воздуха, то такое вращение становится более, чем возможным даже при существенно меньших намагниченностях. При этом углы a и b имеют далеко не оптимальные с точки зрения максимума силы F2τ значения. Величина радиуса R в таких оценках имеет опосредованное значение: все линейные размеры и параметры системы представлены в величинах R. Это позволяет результаты, представленные в настоящей работе считать более или менее универсальными. Основной же результат работы заключается в следующем. Взаимодействие суперпозиции нескольких магнитных моментов с парамагнитной средой действительно должно оказывать влияние на движение одного из них относительно другого. Правда, приведенные выше оценки указывают на существование и других механизмов. Судя по всему лишенным внимания оказался особый характер рассеяния молекул воздуха намагниченной поверхностью твердого тела [5]. К сожалению, добавить тут нечего: это явление недостаточно изучено не только экспериментально, но и теоретически.
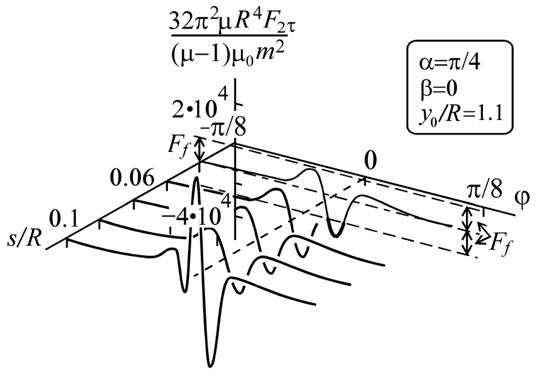
Рис. 3. Тангенсальная составляющая силы, действующей на магнитный момент m2, как функция угла поворота φ и размера сферической полости s
Список литературы
- Тамм И.Е. Основы теории электричества. - М.: ГИТТЛ, 1954. - 620 с.
- Герасимов С.А. Поверхностный молекулярный ток однородно намагниченного тела. // Вопр. приклад. физ. - 2006. - № 13. - С. 57-58.
- Brady M. Permanent Magnetic Motor. Patent WO 045333 A1. 2006.
- Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. - М.: Наука, 1982. - 624 с.
- Берд Г. Молекулярная газовая динамика. - М.: Мир, 1981. - 318 с.
Библиографическая ссылка
С.А. Герасимов ПАРАМАГНИТНОЕ ВРАЩЕНИЕ // Современные наукоемкие технологии. – 2010. – № 8. – С. 26-34;URL: https://top-technologies.ru/ru/article/view?id=25267 (дата обращения: 20.04.2024).