(1)
где 
, 
, 
безразмерные время и координата, t0, x0 - характерные время и масштаб, 
, Χ - коэффициент температуропроводности, 
- начальная температура. Входящие в (1) производные дробного порядка определены следующим образом
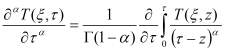- производная Римана-Лиувилля
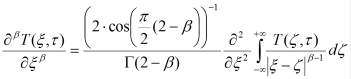- производная Рисса-Вейля
Здесь Г(z) - гамма-функция Эйлера. Производная Римана-Лиувилля учитывает память (нелокальность во времени), производная Рисса учитывает пространственные корреляции (пространственная нелокальность).
Для решения уравнения (1) применим преобразование Фурье по координатной переменной ξ. Получим
(2)
Здесь 
Фурье-образ функции 
. Совершая преобразование Лапласа по переменной 
уравнение (2) дает
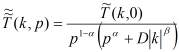(3)
где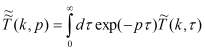 
образ Лапласа функции 
. Совершая преобразование Меллина получим следующее выражение для
, (4)
где 
Функция Миттаг-Леффлера. Совершая в (4) обратное преобразование Фурье окончательно получим решение уравнения (1) в виде
(5)
Решение (5) если α = 1 и β = 2 соответствует решению традиционного уравнения теплопроводности. Действительно, для случая α = 1 имеем 
и (5) принимает вид
(6)
Полагая в (6) β = 2 получим известное решение. Решение (6) для случая 1 < β < 2 учитывает пространственные корреляции. Если в (5) положить β = 2 а 0 < α < 1 то получим решение соответствующее учету эффектов памяти
(7)
В общем случае уравнение (1) имеет новый класс решений, занимающий промежуточное положение между релаксационным и волновым поведением. Эти решения имеют квазиволновой характер. Другая особенность полученных решений в том, что они приводят к степенной зависимости от аргументов. В частности для случая, когда 
для 
имеем
,
а для 
получим 
.
СПИСОК ЛИТЕРАТУРЫ:
- Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск. «Наука и техника», 1987.
- Нахушев А.М. Элементы дробного исчисления. М: Физматгиз, 2003.
- Мейланов Р.П. Обобщенное уравнение одномерной фильтрации с дифференцированиями дробной степени//ИФЖ. 2001. т.74. №2. с.1-4
- Мейланов П., Янполов М.С. Особенности фазовой траектории фронтального осциллятора.// «Письма в ЖЭТФ» 2002.т.28.Вып 1. С.67-71.
- Мейланов Р.П., Свешникова Д.А., Шабанов О.М. Метод дифференциальных уравнений в описании кинетики сорбций // ЖФХ. 2003. Т.77. С.260-264.
- Учайкин В.В. Автомодельная аномальная диффузия и устойчивые законы // УФН. 2003. Т.173, №8.С.846-876.
Библиографическая ссылка
Мейланов Р.П., Шабанова М.Р. УРАВНЕНИЕ ТЕПЛОПРОВДНОСТИ ДЛЯ СРЕД С ФРАКТАЛЬНОЙ СТРУКТУРОЙ // Современные наукоемкие технологии. – 2007. – № 8. – С. 84-85;URL: https://top-technologies.ru/ru/article/view?id=25252 (дата обращения: 21.11.2024).