Гальваностатический режим можно представить системой уравнений (1)-(5) [1]. Постоянство потока ионов на границе электролит-окисел определяется уравнением (1). Изменение концентрации подвижных ионов в окисле происходит в результате диффузионного и миграционного перемещения (2). На границе окисла и металла подвижные ионы вступают в химическую реакцию (3), которая определяет увеличение толщины слоя (4). Уравнение (5) учитывает поле в диэлектрике, образованное заряженными ионами.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() , (5)
, (5)
где c(x,t) - концентрация подвижных ионов в окисле, D, μ - соответственно коэффициент диффузии и подвижность ионов, Ε - напряженность электрического поля, к - химическая константа скорости роста окисла, MOX - молярная масса образующегося оксида, ρOX - плотность оксида, NA - число Авогадро, nox - валентность реакции образования окисла, Εвн - напряженность электрического поля подвижных ионов.
Граничное условие определяется постоянной плотностью потока. Потенциал поля подвижных ионов находится из уравнения Пуассона. Напряженность поля в окисле определяется выражением (6):
![]() . (6)
. (6)
На границе металл-окисел должны выполнятся условия непрерывности дрейфового, диффузионного потока и скорости реакции jдр = jдиф =jхр. Решение системы позволяет воспроизводить кинетические зависимости роста напряжения от времени U(t) для разной плотности тока j (рис 1). Подвижность имеет значение μ = 4∙10-13 м2/В∙с, коэффициент диффузии определяется соотношением Эйнштейна μp/Dp = e/kT.
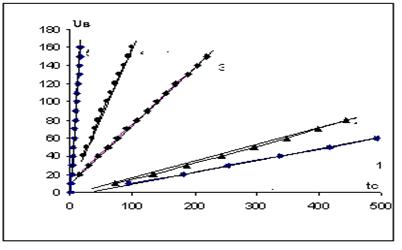
Рис. 1. Зависимость напряжения от времени для различных плотностей тока: 1) 0.5 mA/cm2, 2) 1 mA/cm2, 3) 3 mA/cm2, 4) 5 mA/cm2, 5) 10 mА/cm2
Численный расчет кинетических зависимостей роста напряжения в процессе окисления поверхности тантала проведен на основе системы уравнений (1) - (5). На рис.1 представлены теоретические и экспериментальные кинетические зависимости роста напряжения для различных значений плотности тока j. В процессе моделирования из условия наилучшего согласования экспериментальной и теоретической зависимости подбирались следующие параметры: величина и скорость роста окисла за счет химической реакции k, распределение и концентрация подвижного заряда c(x,t), изменение потенциала φ и напряженности поля Е в окисле.
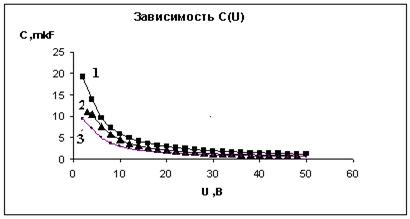
Рис. 2. Зависимость емкости структуры Та -Та2О5 - электролит от напряжения формовки. 1) 0.2 mА/см2, 2) 0.4 mА/cm2 3) 0.8 mА/cm2.
В результате расчетов при µ = 5.6∙10-13м2/В∙с получена постоянная скорости роста для химической реакции k = (2-5)∙10-5 м/с.
Для разных плотностей тока рассчитаны зависимости скорости реакции и распределение поля в окисле Ta2O5. Рассчитано изменение диффузионного поля и потенциала, возникающего за счет разности концентраций на границе окисел-металл. Величина поля в области диффузии ЕD = 1∙108В/м и составляет 10% от внешнего поля, потенциал φD имеет значение порядка 0.001В. Показано, что в веществах с подвижностью больше µ = 5.6∙10-15м2/В∙с проявляется внутреннее поле носителей заряда.
Показано, что емкость, измеренная в процессе анодного окисления, совпадает с рассчитанной емкостью диффузионного слоя на границе металл-окисел.
Представленная модель позволяет объяснить искривление Тафелевских зависимостей U от log j [2] полем диффузионного барьера на границе металл-окисел при увеличении плотности тока и толщины окисла. Зависимость подвижности и коэффициента диффузии согласно соотношению Эйнштейна определяет постоянство тока и напряженности поля, а, следовательно, и наклона зависимости Тафеля от температуры.
СПИСОК ЛИТЕРАТУРЫ:
- Н.А. Авдеев, Г.С. Сиговцев. "О математических моделях процессов анодного окисления"// Труды Петрозаводского государственного университета: сер. Прикладная математика и информатика. Вып.9./ Под.науч. ред. проф. В.И. Чернецкого // ПетрГУ. Петрозаводск, 2000, с 57.
- Л. Юнг "Анодные окисные пленки" //Л.:Энергия, 1967.
Библиографическая ссылка
Авдеев Н.А. Гуртов В.А. Федосеев А.А. ОПРЕДЕЛЕНИЕ КИНЕТИЧЕСКИХ ПАРАМЕТРОВ В ДИФФУЗИОННО-ДРЕЙФОВОЙ МОДЕЛИ АНОДНОГО ОКИСЛЕНИЯ // Современные наукоемкие технологии. 2007. № 8. С. 59-60;URL: https://top-technologies.ru/ru/article/view?id=25233 (дата обращения: 04.03.2026).



