Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Безнос О.С.

Статья в формате PDF

270 KB

В математическое описание предметной области включим следующие основные компоненты БД МИС: множество пользователей , множество пользовательских функции , множество задач обработки данных для подготовки документов , множество групп распределения прав доступа пользователей , множество информационных потоков предметной области , множество отношений между компонентами  - .

В качестве структурных элементов модели предметной области возьмём элементы множеств  и V. Полное множество структурных элементов обозначим через 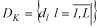, L=M+L_вх+L_вых.

Под матрицей семантической смежности B_k будем понимать квадратную бинарную матрицу, проиндексированную по обеим осям множеством структурных элементов D_k и содержащую запись , если на основании информации пользователей о семантической связности элементов k-го требования, между структурными элементами d_i и d_j существует отношение R такое, что элемент d_i составляет смысловое содержание элемента d_j и -в противном случае.

Для выявления взаимосвязей между структурными элементами, выделения групп информационных элементов и определения их состава с использованием матрицы B_k формируется матрица семантической достижимости A_k=(a_ij).

Под матрицей достижимости A_k будем понимать квадратную бинарную матрицу, проиндексированную одинаковым образом по обеим осям множества структурных элементов . Запись a_ij=1 матрицы A_k соответствует наличию или смыслового отношения достижимости R₀ элемента d_j из элемента d_i, d_iR_od_j. При этом считается, что элемент d_j семантически достижим из элемента d_i, если на графе G существует путь от вершины d_i к вершине d_j, имеющий определенное смысловое содержание.

Матрица A_k даёт возможность определения множеств предшествования C(d_i) и достижимости F(d_i)  d_i D_k . Множество C(d_i) формируется из элементов, соответствующих единичным записям в i-м столбце, а множество F(d_i) - из элементов, соответствующих единичным записям в i-й строке матрицы A_k. Анализ множеств C(d_i) позволяет выделить базовые типы структурных элементов, из которых конструируются информационные элементы и группы. Информационным элементам соответствуют те элементы, для которых C(d_i)=0. На графе G_k им соответствуют висячие вершины. Такой вершиной является вершина d₅ .Значит, множество информационных элементов состоит из одного элемента d₅, обозначим: .

Группа  ∈  принадлежит множеству групп верхнего уровня p₁, если F(d_i^г)∩C(d_i^г)=F(d_i^г).

Для БД МИС имеем: F( d_i^г)∩C(d_i^г)=F(d_i^г), для , p₁ = {d₁^г , d₆^г - d₆₄^г }.

Принадлежность остальных групп уровням иерархии p_m, m≥ 2 определяется итеративным образом из соотношения:p_m={d_i^г ∈ D_k^г p₁...p_m-1/F_m-1( d_i^г)∩C_m-1(d_i^г )=F_m-1(d_i^г )}, где F_m-1(d_i^г ) и C_m-1( d_i^г) соответственно множества достижимости и предшествования групп d_i^г ∈ D_k^г   на подмножестве D_k^г p₁...p_m-1. Исходя из этого, получим: p₂ = { d₂^г}, p₃ = {d₃^г }, p₄ = {d₄^г }.

Упорядочение групп позволяет выделить группы, являющиеся корневыми группами структуры и группы, занимающие промежуточное положение. Корневые группы определяют возможные точки входа в информационную структуру, а промежуточные расширяют сведения об информации, помещенной в корневых и вышележащих группах.

Таким образом, рассмотренная выше методика анализа информационных требований пользователей позволяет благодаря выделенным группам упростить исходную матрицу. Это упрощает дальнейший анализ предметной области.

СПИСОК ЛИТЕРАТУРЫ:

1. Кульба В.В., Ковалевский С.С., Косяченко С.А., Сиротюк В.О. Теоретические основы проектирования оптимальных структур распределённых баз данных. Серия «Информатизация России на пороге XXI века». - М.:СИНТЕГ, 1999, 660 с.

Библиографическая ссылка