Система состоит из резервуара, в котором в начальный момент времени τ =0 находится водомазутная эмульсия массой М0 и температурой tх и параллельно соединенных подогревателей. В ходе циркуляционного подогрева водомазутной эмульсии из резервуара выходит поток с расходом G0 и температурой t. Поток из резервуара направляется в узел разделения, где делится на части с соответствующими расходами, далее потоки направляются в соответствующие узлы смешения на входах в подогреватели. В подогревателях водомазутная эмульсия подогревается от температуры tвхпj до температуры tвыхпj. На выходе из j-го подогревателя поток вновь делится на части. Одна часть с расходом Gвыхj направляется к узлу смешения потоков и далее к резервуару, другая часть с расходом Gjj направляется с выхода подогревателя на его вход, а третья c расходом Gкj к узлу смешения и далее к котлам. Из резервуара выходит поток водомазутной эмульсии с заданным расходом Gдр, который направляется к другим видам оборудования. Кроме того, в резервуар могут подаваться потоки от другого оборудования (например, со сливной эстакады) с заданными расходами Gпост и с заданными температурами tпост.
Примем следующие основные допущения:
- Время тепловой релаксации вследствие быстрого перемешивания в резервуаре много меньше рассматриваемых промежутков времени, на которых происходит существенное изменение температуры водомазутной эмульсии, т.е. процесс подогрева квазистационарный и температура в резервуаре является функцией времени τ (не зависит от его объема);
- Теплофизические характеристики жидкости в рассматриваемом интервале температур подогрева меняются незначительно.
Масса водомазутной эмульсии в резервуаре является функцией времени τ и может быть представлена в виде:
. (1)
Уравнение теплового баланса для резервуара за период времени dτ имеет следующий вид:
,(2)
где 
- количество теплоты необходимое для подогрева жидкости в резервуаре до заданной температуры; 
- количество теплоты, отдаваемое или получаемое жидкостью в резервуаре от другого оборудования; срм - удельная теплоемкость водомазутой эмульсии; 
- количество теплоты, отводимое из резервуара к подогревательному блоку;
- потери теплоты в окружающую среду; k - коэффициент теплопередачи в окружающую среду; F - площадь поверхности резервуара;t o.c - температура окружающей среды.
В результате ряда преобразований уравнение (2) запишется в виде:
.
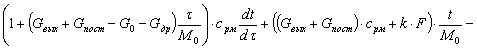(3)
К уравнению (3) необходимо добавить начальные условия:
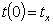(4)
Уравнение (3) совместно с начальным условием (4) является базовым уравнением для описания процесса подогрева водомазутной эмульсии в резервуаре.
В ходе решения поставленной задачи определяются температурно-временные зависимости t (τ) из решения задачи Коши для обыкновенных дифференциальных уравнений совместно с начальным условием (4).
Разработана математическая модель теплогидравлических процессов происходящих при подогреве водомазутной эмульсии в системах из резервуара и параллельно соединенных подогревателей.
В пределах разработанной математической модели, также были рассмотрены конкретные задачи о нахождении зависимостей температуры в резервуаре от времени подогрева при заданных расходах для различных режимов хранения и подготовки водомазутной эмульсии к сжиганию.
Библиографическая ссылка
М.Ф. Шагеев, С.А. Лившиц, Э.М. Хайриева МОДЕЛИРОВАНИЕ ПОДОГРЕВА ВОДОМАЗУТНОЙ ЭМУЛЬСИИ В ТЕХНОЛОГИЧЕСКИХ СХЕМАХ // Современные наукоемкие технологии. – 2010. – № 7. – С. 161-163;URL: https://top-technologies.ru/ru/article/view?id=25085 (дата обращения: 21.11.2024).