Предлагаемая математическая модель содержит три группы уравнений. Первую группу уравнений составляют дифференциальные уравнения равновесия, которым должны удовлетворять компоненты напряженного состояния. На границах рассматриваемых объектов напряжения должны удовлетворять статическим граничным условиям. Вторую группу уравнений образуют уравнения совместности деформаций. На границах перемещения должны удовлетворять кинематическим граничным условиям.
Уравнения равновесия и уравнения совместности деформаций не зависят от физико-механических свойств материала и условий нагрева. Для расчета рассматриваемых конструкций шаговым методом эти уравнения и граничные условия записываем в приращениях:
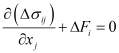 , (1)
, (1)
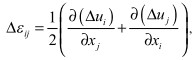 , (2)
, (2)
![]() , (3)
, (3)
![]() . (4)
. (4)
Третью группу уравнений составляют уравнения пластического течения, связывающие напряжения и деформации. Их конкретный вид определяется применяемой теорией пластичности и принятой для расчета математической моделью кинетики процесса упругопластического деформирования конструкционного материала. В данной работе уравнения пластического течения материала, связывающие приращения напряжений и деформаций в процессе нагружения конструкции, получены на основе соотношений теории неизотермического пластического течения с трансляционным и изотропным упрочнением [1]:
![]() (5)
(5)
Первое слагаемое в матричном уравнении (5) определяет приращения упругой и пластической деформаций, связанные с ростом напряжений, второе слагаемое - приращения деформаций, вызванных изменением температуры. ![]() - матрица коэффициентов упругости;
- матрица коэффициентов упругости; ![]() - матрица коэффициентов пластичности; вектор
- матрица коэффициентов пластичности; вектор ![]() характеризует скорость изменения деформаций, вызванных изменением температуры ΔT.
характеризует скорость изменения деформаций, вызванных изменением температуры ΔT.
При решении задачи в главных осях напряженно-деформированного состояния:
![]() ;
; ![]() ;
; ![]() - символ транспонирования;
- символ транспонирования;
![]() =
= ![]()
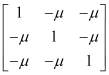 ;
; ![]() =
= 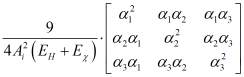 ;
;
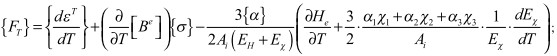 ;
;
![]() =
= ![]() ;
; 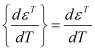 [1 1 1]T ;
[1 1 1]T ;
![]() ,
, ![]() - активные напряжения;
- активные напряжения;
![]() ,
, ![]() - компоненты девиатора напряжений;
- компоненты девиатора напряжений;
![]() ,
, ![]() - остаточные микронапряжения, характеризующие смещение центра упругой области на обобщенной диаграмме деформирования вследствие пластической деформации;
- остаточные микронапряжения, характеризующие смещение центра упругой области на обобщенной диаграмме деформирования вследствие пластической деформации;
![]() - интенсивность активных напряжений;
- интенсивность активных напряжений;
![]() ,
, ![]() ;
;
![]() - мгновенная ширина упругой области на обобщенной диаграмме деформирования;
- мгновенная ширина упругой области на обобщенной диаграмме деформирования; ![]() и
и ![]() - мгновенные пределы текучести при прямом и обратном деформировании;
- мгновенные пределы текучести при прямом и обратном деформировании;
![]() - остаточные микронапряжения при одноосном напряженном состоянии;
- остаточные микронапряжения при одноосном напряженном состоянии;
![]() - накопленная пластическая деформация (параметр Одквиста);
- накопленная пластическая деформация (параметр Одквиста);
Систему уравнений (1)-(5) можно рассматривать как математическую модель кинетики процесса упругопластического деформирования, отражающую с достаточной полнотой характерные особенности работы элементов конструкций в условиях нестационарного термомеханического нагружения.
СПИСОК ЛИТЕРАТУРЫ:
-
Термопрочность деталей машин. Под ред. И.А.Биргера и Б.Ф.Шорра. М., "Машиностроение". 1975. 455 с., ил.
Библиографическая ссылка
Дорофеева И.А., Луганцев Л.Д., Саитова Я.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЦИКЛИЧЕСКОГО УПРУГОПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ // Современные наукоемкие технологии. 2007. № 6. С. 100-102;URL: https://top-technologies.ru/ru/article/view?id=25070 (дата обращения: 13.03.2026).



