30 лет назад предполагалось, что в низкотемпературных химических и плазмохимических процессах выполняются метод Борна-Оппенгеймера и принцип Франка-Кондона, однако сегодня многие специалисты полагают, что соблюдение принципа Франка-Кондона является скорее исключением из правил. Знание фактора Франка-Кондона необходимо для определения такого важного параметра низкотемпературных процессов, какой является колебательная температура.
В работе [1] приведено описание аномалий во вращательной структуре радикала С2. В данной работе ставилась задача изучения изменений колебательной структуры электронных спектров радикала С2 при активном протекании химических реакций в плазме и возможности определения колебательной
температуры радикала С2 по эмиссионному спектру.
Экспериментальная установка состояла из коаксиального плазмотрона, состыкованного с медной охлаждаемой кюветой (длиной 0,3 м и диаметром 0,12 м) и теплообменником. В кювете имелись окна из плоского кварца, обдувались аргоном через 24 радиальных отверстия. Плазмотрон работал на газе CF .
В проведенных ранее в работе [2] экспериментах определение колебательной температуры производилось по секвенции Δv= - 1. Как и в работе [2], измерения были основаны на следующем предположении: общая интенсивность полос пропорциональна пикам интенсивности в кантах. Для дугового разряда в кварцевой трубке в атмосфере газа CF4 и для условий, реализующихся в медной камере с оптическими окнами и расположенной после плазмотрона, наблюдает ся хорошая линейная зависимость между lg(I/qv`v``) и колебательным термом G(v´), где qv`v`` - фактор Франка-Кондона. Эта зависимость рассматривалась в работе [3]. В ней уже упоминалось, что аномалии в колебательной структуре секвенции Δv= + 1 наблюдались при определенных условиях, например во фторуглеродной плазме при понижении поступательной температуры до 4000 К и ниже. В этом случае в плазме становилось возможным протекание химических реакций с образованием многоатомных молекул. Селективную убыль радикала С , имеющего аномалии в колебательной структуре электронного спектра, в данном случае можно объяснить химическими реакциями. При дуговом разряде между угольны
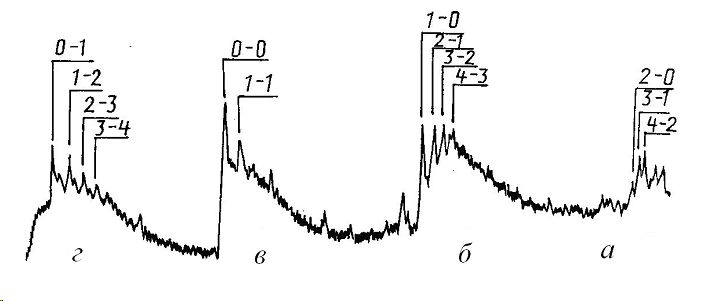
Рис.1 Колебательная структура спектра испускания радикала С2: Δv = - 1(а), 0 (б), 1 (в) и 2 (г)
ми электродами в среде аргона наблюдается экспоненциальное распределение частиц по энергетическим уровням. В работе [4] приводятся данные для радикала С2 , спектр которого фотографировался от кислородноацетиленовых пламен. Интенсивность перехода 0-0 секвенции Δv = 0 принимается за 10 отн. ед. и интенсивность максимальной
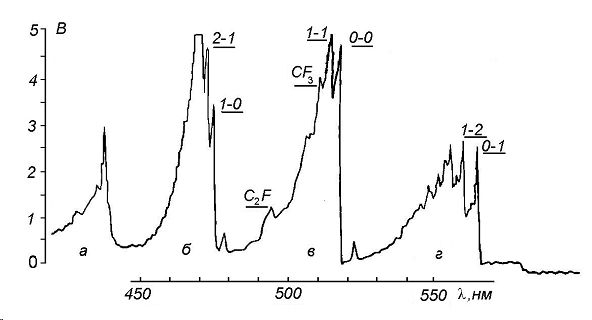
Рис. 2 Общий вид аномалий в колебательной структуре радикала С2 : Δv = 2 (а), 1 (б), 0 (в) и - 1 (г).
для всех переходов в системе полос Свана (переход d3Πg - a3Πu).
На рис.1 представлена система полос Свана, наблюдаемая в дуговом разряде а аргоне. Соотношение интенсивности полос в спектре близко к соотношению, описанному гейдоном для пламен [4]. Спектры регистрировались на комплексе КСВУ-23 с обратной линейной дисперсией 1,6 нм/ мм. Источником света служила кварцевая кювета, расположенная за плазмотроном. Предполагалось, что потеря системой световой энергии должна привести к своеобразной световой закалке плазмы и повлиять на химическую активность радикала С2 (под закалкой плазмы понимается резкое понижение температуры). Данные хромато- графического анализа показали на выходе теплообменника наличие продуктов C2F4 и C2F6 до 1% от общего количества газа, в то время как при обычной закалке эти продукты отсутствовали. Из этого следовало, что в кварцевой кювете идут процессы, отличные от тех, которые протекают при закалке в медных теплообменниках при охлаждении проточной водой. Изменения в спектре оказались значительнее, чем ожидалось, и требуют серьезного изучения. В данной работе предполагалось, помимо описания наблюдаемых аномалий, дать предварительный анализ наблюдаемого явления.
На рис.2 представлен характерный спектр радикала С2 с разрешенной колебательной структурой. Рассматриваются 4 секвенции (Δv = -1, 0, +1, +2). В данной работе рассмотрение будет проводиться в соответствии с систематизацией, проведенной Гейдоном.
В соответствии с этой систематизацией переход 0–0 секвенции Δv = 0 (рис.2) должен быть самым интенсивным. Его интенсивность принимается за 100 %. В действи- тельности переход 1 – 1, который дожжен составлять 60 % от интенсивности перехода 0–0, значительно превосходит его по интенсивности (сравни с рис.1). Интенсивность перехода 1–0 секвенции Δv = +1 должна составить 90% от интенсивности перехода 0–0. (рис. 2) и должна быть максимальной в указанной секвенции. В действительности это самая слабая полоса в секвенции Δv = + 1. Наблюдается четко выраженная инверсная заселенность уровней данной секвенции. Максимальная интенсивность полос переходов 4–3 и 3–2 секвенции Δv = +1 значительно превосходит интенсивность полос в секвенции Δv = 0. Интенсивность полос секвенции Δv = –1 совпадает с интенсивностью полос секвенции Δv = +2, хотя в действительности последняя должна быть слабее на 30%. Теперь рассмотрим наблюдаемую аномалию с другой стороны. Возьмем верхний уровень один и тот же для ряда переходов, допустим, первый. Верхний уровень для всех указанных актов испускания один и тот же. Следовательно, возмущение, оказываемое плазмой на данный уровень, без учета вероятности переходов должно быть одинаковым. Интенсивность переходов по отношению к перехо- ду 0-0 должна быть следующей: 1–0 90%, 1–1 60% и 1–2 80%. В действительности распределение интенсивности пиков: 1–0 60%, 1–1 100%, 1–2 55%. Возможны два объяснения. Первое – изменение обусловлено изменени- ем общей волновой функции, которая условно равна Ψ = ΨelΨvibΨrot, и изменяется ком- бинационное соотношение между уровнями. Второе — протекают химические реакции, которые инициируют переходы с различных уровней с неодинаковой вероятностью. На рис. 2 приводятся слабые пики радикалов C2F и CF3, что как раз свидетельствует о протекании химических реакций в этих условиях.
На рис. 3 представлена секвенция Δv = + 1 радикала С2. В этой секвенции наиболее ярко выражено различие между интенсивностями переходов, приведенных на рис. 3 и теми, которые приводятся Гейдоном (см. рис. 1).
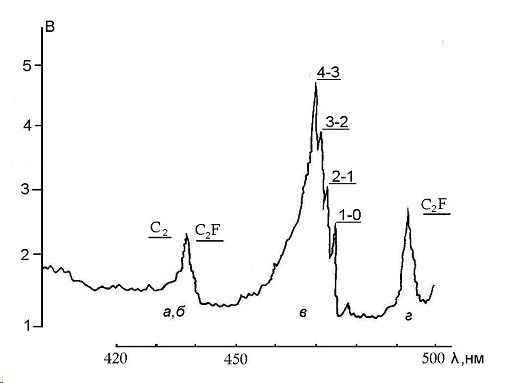
Рис.3. Эмиссионный спектр радикала С2 и аномалия в секвенции Δv = + 1 этого же радикала, Δv = 2(а,б), 1(в) и 0 (г)
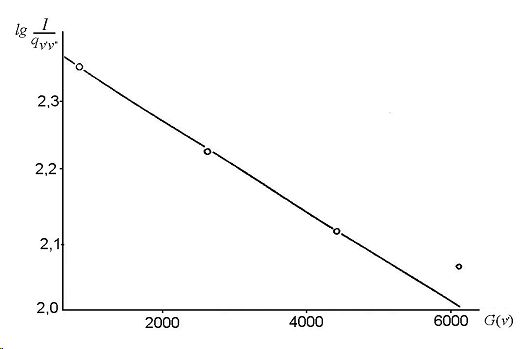
Рис.4. Определение колебательной температуры по радикалу С2. Аргоновая низкотемпературная плазма. Тvib = 4500 К. Секвенция Δv = –1
Помимо секвенции Δv = + 1 радикала С2, на рис. 3 пред ставлены две интенсивные секвенции радикала C2F (Δv = 0, +2). Сек венция Δv = + 2 радикала C2F накладывается на секвенцию Δv = +2 радикала С2. Полосы в секвенции имеют различные оттенения, что сказывается на контуре полосы. Секвенция Δv = 0 радикала C2F на рис. 3 обозначена буквой г.
Что касается полной волновой функции, ее можно представить в виде произведения отдельных волновых функций в соответствии с методом Борна-Оппенгеймера, а фактор Франка-Кондона представляет собой вероятность перехода соответствующих колебательных переходов и его можно представить формулой
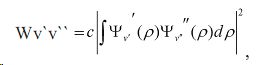 ,
,
где Wv`v`` — фактор Франка-Кондона, ρ – величина межъядерного расстояния и Ψv` — колебательная электронно-волновая функция верхнего колебательного состояния. В практических целях величина фактора Франка-Кондона рассчитывается теоретических для всех комбинирующих состояний. На рис. 4 представлена зависимость величины lg(I/qv`v``) от колебательного терма G(v`). Как видно из рисунка, хорошая линейная зависимость говорит не только о хорошем приближении выполненных расчетов, но и о выполнении принципа Франка-Кондона
Температура как термодинамическая величина, характеризующая энергетическое состояние макроскопической системы, применима к системам, находящимся в равновесных условиях либо близких к равновесным. В химически активной плазме, в частности, фторуглеродной, наблюдается неравновесное распределение энергии по степеням свободы. И поэтому температура как целостное понятие теряет свой физический смысл. Можно говорить о температуре вращательной, колебательной и т. д. и даже о температуре какой-либо группы уровней, принадлежащих одной молекуле [5]. Такие термодинамические величины как энтропия, энтальпия, теплоемкость, потенциал гиббса выражаются через температуру, а константа реакции определяется термодинамическими потенциалами.Так как единой температуры в химически активной плазме не существует, то нарушается связь температуры с термодинамическими потенциалами и, следовательно, вытекают дополнительные возможности влияния на протекание химических реакций. То есть в некоторых случаях становится целесообразным создание неравновесных условий, чтобы прошли те реакции, которые желательно провести.
В соответствии с термодинамическим расчетом, приведенным в работе [3], во фторуглеродной плазме при описанных условиях должны наблюдаться спектры радикалов CF, CF2 , CF3 . Система полос, отнесенная к радикалу CF3, зафиксирована также и в области 200 нм. Спектр имеет тот же вид, что и секвенция Δv = 0, и наблюдался ранее [5]. Спектры радикалов CF и CF3 были зарегистрированы в испускании. Спектр радикала CF2 в испускании зафиксировать не удалось. Таким образом, протекание интенсивных химических реакций в плазме сильно влияет на вид даже относительно простых и хорошо изученных спектров. Потеря световой энергии может усиливать неравновесные процессы.
Некоторое расхождение с термодинамическим расчетом определяется неравновесным распределением энергии по степеням свободы.
В заключение следует отметить так же, что инверсная заселенность электронно- колебательных уровней энергии, приводящая к нарушению принципа Франка-Кондона, отражает тот факт, что электронно-волновая функция системы не может быть представлена в приближении Борна-Оппенгеймера. Волновая функция такой системы не может быть представлена в виде произведения электронной и колебательной волновых функций отражая факт неразрывной связи квантово-механических процессов в электронной структуре свободного радикала С2.
Список литературы
- С.И. Бурдюгов, В.Г. Халтурин. Аномалии во вращательной структуре электронного спектра радикала С2//Химическая физика и мезоскопия. 2009. Т.11, №1. С.126–130.
- В.Г. Халтурин, В.С. Шайдуров. Диагностика фторуглеродной плазмы по эмиссионному спектру радикала С2 //ЖПС. — 1981. — T.XXXV. — №5. — С.770–774.
- В.Г. Халтурин. Спектроскопическое исследование химически активных сред при утилизации супертоксикантов. Пермь. — 2002. — 85с.
- Гейдон А. Энергия диссоциации и спектры двухатомных молекул. М. — 1949. — 467с.
- Masako Suto and Nobuaki Washida // J. Chem.Phys. 1983. V.78.№3. P.1007–1011.
Библиографическая ссылка
В. Г. Халтурин, В. В. Карманов, Н. Ш. Гыйбадуллин ИНВЕРСНАЯ ЗАСЕЛЕННОСТЬ УРОВНЕЙ ЭНЕРГИИ В КОЛЕБАТЕЛЬНОЙ СТРУКТУРЕ РАДИКАЛА С // Современные наукоемкие технологии. 2010. № 6. С. 89-94;URL: https://top-technologies.ru/ru/article/view?id=24966 (дата обращения: 05.03.2026).



