Процесс нанесения обрабатываемого материала на валки при аналогичном механизме течения имеет существенные отличия от наиболее близкого по схеме процесса каландрования полимерных материалов. Прежде всего, вязкость среды на 2-4 порядка ниже вязкости каландруемых полимеров, например, резиновых смесей. Поэтому, если для каландров из-за больших распорных усилий определяющими являются энергосиловые и механические расчеты, то при нанесении на валки составов типа паст или густых суспензий возникающие усилия сравнительно невелики и основным технологическим параметром процесса течения является толщина материала. При этом силы вязкого трения соизмеримы с силами собственного веса жидкости. Подробный обзор работ, посвященных течению ньютоновских жидкостей в валковом зазоре, дан в работах [1, 2].
Цель работы - постановка задачи течения ньютоновской среды в зазоре вращающихся валков с учетом сил собственного веса жидкости.
Схема течения и система координат представлены на рис.1. Начало декартовой системы координат помещено в середине сечения минимального зазора. Ось у направлена горизонтально, ось x - вертикально вниз. Уровень жидкости x = x0 постоянен. Объемный расход жидкости G. Окружная скорость
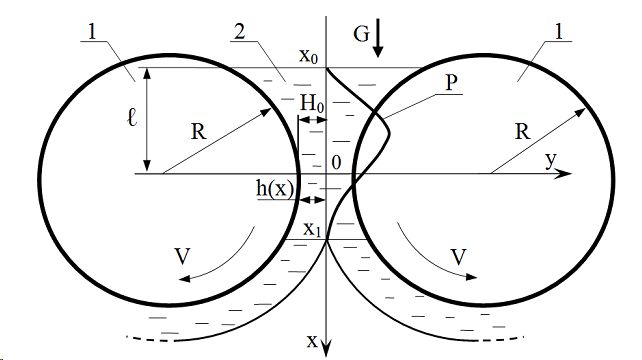
Рис.1. Схема течения вязкопластической среды в вертикальном зазоре между валками:1 - валки, 2 - жидкость, 3,4 - первая (противотока) и вторая (прямотока) зоны вязкопластического сдвигового течения, 5 - квазитвердое ядро.
валков V, их радиус R. Минимальный зазор между валками 2H0 , а текущий 2h. Полагаем, что валки имеют достаточную длину, пренебрегая тем самым течением материала вдоль валков (задача квазиплоская). Окружные скорости валков одинаковы (задача симметричная), но малы и силы инерции не учитываем. Физические свойства жидкости не зависят от температуры и давления. Величина минимального межвалкового зазора мала по сравнению с радиусом кривизны валков (2H0 << R). Давление изменяется по длине зоны течения (∂p/∂y = 0). Среда описывается ньютоновской реологической моделью (τ = η(∂υ /∂y)). Направление течения сверху-вниз.
В качестве модельного объекта, вследствие его доступности для исследований, выбрана валковая сушилка, работающая на ОАО «Волжский Оргсинтез» для сушки изобутилового ксантогената калия (R = 0,6 м,H0= 10-3 м). На сушку подается сравнительно малоконцентрированная суспензия (содержание твердой фазы 4 % об., 9 % масс.),поэтому возможен процесс гравитационного разделения (отстаивания) твердой фазы в зоне течения. Это может привести к неоднородной концентрации частиц по объему зоны течения и существенному изменению реологических свойств суспензии и картины ее течения в валковом зазоре.
Пусть: диаметр частиц dч = 10 -5 м, плотность частиц ρт = 1400 кг/м3, жидкости ρж = 965 кг/м3; при температуре 45 °С вязкость бутилового спирта ηсп = 1,7·10-3 Па·с, вязкость воды ηв = 0,7·10-3 Па·с, вязкость суспензии η ≈ 1,4·10-3 Па·с.
Найдем скорость свободного осаждения частицы по формуле Стокса:
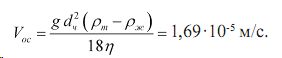
Высота зазора описывается параболой [3]: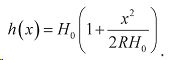
.
Для валка единичной ширины объем жидкости равен:
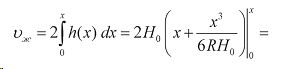4,41·10-5 ÷ 1,70·10-2 м2.
Объем жидкости за минимальным зазором не учитывался.
Уровень жидкости в зависимости от изменения частоты вращения валков в пределах n = 4 ÷ 12 мин-1, рассчитанный по модели, составляет ℓ = 0,02 ÷ 0,31 м.
Пусть скорость жидкости на выходе равна окружной скорости валка. Можем записать для граничных значений с учетом напорного эффекта формулу для расчета двухмерного расхода жидкости:
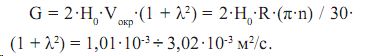
Следовательно, время пребывания жидкости в валковом зазоре:
tпр = υж / G = 0,03 ÷ 16,91 с.
Путь осаждения частицы (или ее вертикальное перемещение) ℓос за время пребывания составит:
ℓос = Vос / τпр = 1,00·10-6 ÷ 1,13·10-3 м.
Поскольку ℓос << ℓ, то изменением однородности реологических свойств жидкости в зазоре вследствие осаждения можно пренебречь.
Кроме того, однородности распределения частиц способствует циркуляция жидкости в рабочем зазоре, обусловленная противотоком на входе. Тепловая оценка процесса течения в валковом зазоре особенно важна для валковых сушилок. Материал на сушку подается при температуре ~ 45 °C. Температура поверхностей валков ~ 87 °С. Поэтому существует тепловой поток к материалу от поверхности валков. Предполагая, что течение у поверхности валка отсутствует, найдем глубину проникновения тепла в жидкость. Время теплового контакта жидкости с поверхностью валка в зоне течения (до выхода из зазора) составляет:
t ≈ ℓ / Vокр = (ℓ·30) / (R·π·n) = 0,05 ÷ 1,23 с.
Глубину проникновения тепла δ, предполагая жидкость полубесконечной толщины и пренебрегая кривизной поверхности валка, найдем по формуле (принимая для суспензии коэффициент теплопроводности μж = 0,4 Вт/(м·К), теплоемкость сp = 2,33 кДж/(кг·К)):
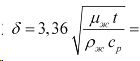3,17·10-4 ÷ 1,57·10-3 м.
Следовательно, только в окрестности минимального зазора толщина прогрева достигает величины порядка миллиметра. Таким образом, размер зоны термического воздействия поверхности валка значительно меньше размеров зоны течения жидкости в клинообразном зазоре, поэтому изменением однородности реологических свойств жидкости в зазоре вследствие ее нагревания можно пренебречь.
В направлении оси z течение отсутствует (квазиплоская задача), поэтому дифференциальные уравнения Навье–Стокса для описания движения вязкой жидкости имеют вид:
Полное описание движения получают путем анализа уравнений Навье–Стокса совместно с уравнением неразрывности потока:
.
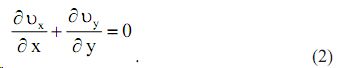Изменим форму уравнения неразрывности. Выделим в зоне течения криволинейную трапецию, ограниченную сечениями х и х1. Определим поток вектора скорости через замкнутый контур, проинтегрировав уравнение (2) по высоте зазора:
.
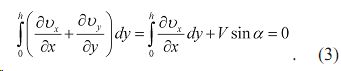В выражении (3) учитывались граничные условия для поперечной скорости. Далее, учитывая соотношения:
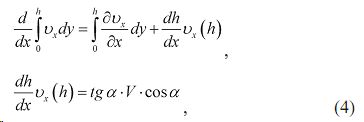
и подставляя соотношения (4) в (3), получим интегральное уравнение неразрывности
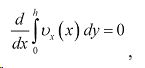
, или
где G — постоянная. Согласно полученному выражению объемный расход жидкости для валка единичной ширины G постоянен по длине зоны течения.
Выполним методом малого параметра оценку членов уравнений движения. Характерными размерами зоны течения (масштабами) являются: в направлении оси х — продольный размер ℓ, в направлении у – минимальный зазор H0. Введем параметры и безразмерные переменные:
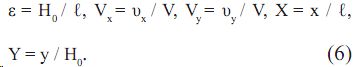
С учетом параметров (6) уравнения движения (1) примут вид:
Для поперечной скорости в конвективных слагаемых уравнений используем ее представление через осевую скорость из уравнения неразрывности (2). После деления всех членов уравнений (7) на ηV/H0 2 получим безразмерную форму уравнений движения: Ведем рассмотрение задачи в рамках стоксова приближения (Re << 1).
Число Рейнольдса составляет: Re = ε ρVH0 / η = 0,0155.
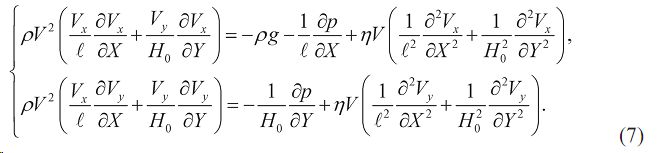
Оценка сил собственного веса жидкости: St = ρgH0 2 / (ηV) = 1,4506. Видно, что силы собственного веса жидкости следует учитывать, поскольку они на два порядка превосходят силы инерции.
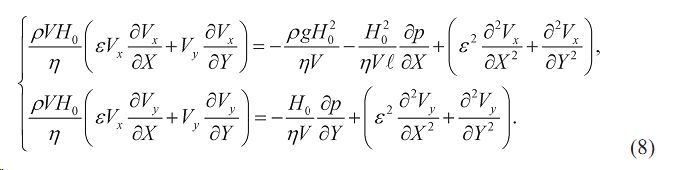
Кроме того, в рассматриваемом случае (H0 ≈ 10-3 м, ℓ ≈ 0,3 м) имеет место неравенство ε << 1. В уравнениях (8) слагаемыми, содержащими множитель ε2, пренебрегаем:
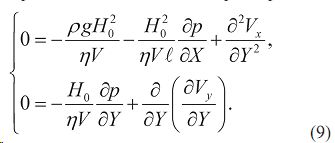
При этом из уравнения неразрывности (2) можем записать:
Обозначим комплекс в первом уравнении движения (9) P = H0 2 p / (ηVℓ) как безразмерное давление. При этом уравнения движения (9) с учетом выражения (10) примут вид:
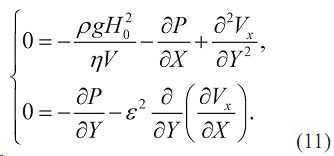
Из полученных уравнений (11) видно, что давление в поперечном направлении (по y) является величиной порядка ε2 и им можно пренебречь. Для описания течения, с учетом принятых допущений, следует использовать первое уравнение движения (1), учитывающее силы собственного веса, давления и вязкого трения. Поскольку давление изменяется только по длине канала, а поле скоростей двумерно это приближение можно назвать квазиплоским.
С учетом принятых допущений течение описывается системой дифференциальных уравнений движения (включая гравитационный член), неразрывности и реологического состояния:
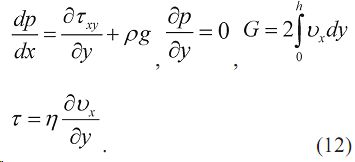
Во входном x = x0 и выходном x = x1 сечениях давление равно атмосферному и без снижения общности полагаем p = 0.
Таким образом, уравнения (12) следует дополнить следующими граничными условиями:
входное сечение
x = x0, p = 0, (13)
условие прилипания
y = h, υx = V, (14)
выходное сечение
x = x1, p = 0, υx = V, τxy(y = h)= 0, (15)
условие симметричности
x0 < x < x1, y = 0, γ = 0, τxy = 0. (16)
Список литературы
- Зубович С.О., Шаповалов В.М. // Известия ВолггТу (сер. реология, процессы и аппараты химической технологии): меж- вуз. сб. науч. ст. — №11(37). — Волгоград, 2007. — С. 33.
- Клинков А.С., Соколов М.В., Кочетов В.И. Автоматизированное проектирование валковых машин для переработки полимерных материалов. — М.: Издательство машиностроение — 1, 2005. — С. 5.
- Мак-Келви Д.М. Переработка полимеров. — М.: Химия, 1965. — С. 230.
Библиографическая ссылка
С. О. Зубович СИММЕТРИЧНОЕ ТЕЧЕНИЕ ТЯЖЕЛОЙ ЛИНЕЙНО-ВЯЗКОЙ СРЕДЫ В ЗАЗОРЕ ВРАЩАЮЩИХСЯ ВАЛКОВ (ПОСТАНОВКА ЗАДАЧИ) // Современные наукоемкие технологии. – 2010. – № 6. – С. 77-82;URL: https://top-technologies.ru/ru/article/view?id=24964 (дата обращения: 21.11.2024).