Поэтому необходим метод учета масштабного фактора при любой длине испытуемого образца, например из древесины ели, сечением 20 × 20 мм, но при длине вдоль волокон древесины менее 300 мм.
Цель статьи - выявить статистические закономерности масштабного фактора акустических показателей древесины вдоль волокон при прохождении ультразвуковых колебаний (УЗК) и показать методику испытания на короткомерных прямоугольных образцах.
Все измерения были выполнены на одном стандартном образце из древесины ели, что позволило исключить влияние свойств самой древесины. Стандартный образец озвучивался ультразвуковым прибором «Пульсар-1.0» при пяти повторах измерений, а затем отпиливался отрезок длиной около 50 мм. После этого остаток длиной 250 мм и отрезок длиной 50 мм снова озвучивали, а результаты измерений записывали. Так продолжали отпиливать от остатка стандартного образца отрезки убывающей длины и измерять время прохождения ультразвука с частотой 60 кгц на датчиках через остатки и отрезки.
Контакт датчиков (излучатель и приемник) прибора «Пульсар-1.0» при плоской поверхности требует высокого качества формы и чистоты обработанной поверхности торцов остатков и отрезков от стандартного образца. Поэтому, по нашему патенту [5], применяли конусные насадки № 2 [7], которые были выбраны в ходе тарировочных испытаний на эталонном образце из оргстекла заводского изготовления, а также на самом испытуемом стандартном образце из древесины ели.
Длина обоих конусных насадок была по 47,4 мм при угле конуса в 42 градуса, причем эти насадки были изготовлены, с посадочными местами (рис. 1) на датчики, из ленгированной стали с закалкой в масле. Насадки просты по конструкции.
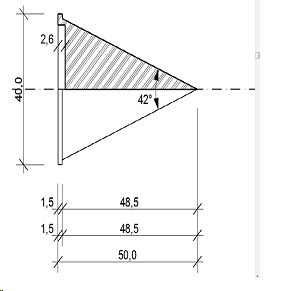
Рис. 1. Конусная насадка № 2 на датчик прибора «Пульсар-1.0»
Стандартный датчик от прибора«Пульсар1.0» в таблице 1 показан под № 0. Он имеет плоскую форму контактной поверхности и угол конуса в 180 град. Для неплоских поверхностей образца соприкосновение должно быть точечным (при пренебрежимо малом углублении в древесину). В насадке № 2, для снижения погрешности измерения по времени прохождения УЗК, цилиндрический участок был исключен с оставлением первоначального угла острия конусной насадки в 42 град. При этом уменьшается общая длина насадки до 47,4 мм.
При тарировке время t (микросекунды) прохождения УЗК через стандартный образец из древесины ели измерялось с тремя повторами.
Таблица 1. Время прохождения УЗК, мкс
|
Излучатель |
Приемник |
|
|
№0 |
№2 |
|
|
№ 0 |
62,7 |
69,8 |
|
62,7 |
69,7 |
|
|
62,8 |
69,8 |
|
|
№ 2 |
70,2 |
78,3 |
|
70,0 |
78,3 |
|
|
70,1 |
78,3 |
|
Сравнение показало, что длина консуной насадки более 35-40 мм удобнее в эксплуатации из-за того, что не мешает измереням на неровной поверхности бесформенных образцов деревсины. Для сертификации древесины в виде образцов неплоской формы, например, поленьев по патенту № 2334984 [5], оказалось удобным угол конуса в 42 град. удобнее применять два одинаковых насадка на датчиках (излучателе и приемнике).
Среднее время УЗК будет равно для датчика № 0 (62,7 + 62,7 + 62,8) / 3 = 62,73 мкс, а эти же датчики с насадками № 2 - (78,3 + 78,3 + 78,3) / 3 = 78,30 мкс. разница между ними составит 78,30 - 62,73 = 15,57 или округленно 15,6 мкс. Потери времени на две конусные насадки № 2, при испытании древесины вдоль волокон, будут равны 15,6 мкс.
Результаты основных испытаний по остаткам и отрезкам от стандартного образца из древесины ели 20 × 20 × 300 мм приведены в данных таблицы 2 и таблицы 3.
Таблица 2. Остатки после отпиливания от стандартного образца
|
№ п/п |
Длина отрезка, мм |
Время УЗК (по повторам), мкс |
|||||
|
теорет. |
фактич. |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
300 |
300,1 |
78,3 |
78,3 |
78,4 |
78,4 |
78,4 |
|
2 |
250 |
249,2 |
69,1 |
69,1 |
69,1 |
69,2 |
69,1 |
|
3 |
200 |
198,9 |
60,6 |
60,5 |
60,6 |
60,6 |
60,5 |
|
4 |
160 |
159,2 |
54,3 |
54,2 |
54,2 |
54,1 |
54,2 |
|
5 |
120 |
118,9 |
49,0 |
49,0 |
48,9 |
48,9 |
49,0 |
|
6 |
100 |
98,7 |
46,6 |
46,5 |
46,5 |
46,5 |
46,5 |
|
7 |
80 |
80,3 |
43,0 |
43,0 |
42,9 |
42,9 |
43,0 |
|
8 |
60 |
59,3 |
34,6 |
34,5 |
34,6 |
34,5 |
34,5 |
|
9 |
40 |
40,4 |
30,6 |
30,6 |
30,6 |
30,6 |
60,5 |
|
10 |
30 |
30,0 |
28,8 |
28,8 |
28,9 |
28,9 |
28,9 |
|
11 |
20 |
20,2 |
27,4 |
27,3 |
27,3 |
27,3 |
27,3 |
|
12 |
10 |
10,9 |
25,8 |
25,9 |
25,8 |
25,8 |
25,8 |
|
13 |
5 |
4,3 |
24,5 |
24,5 |
24,5 |
24,6 |
24,5 |
Общая длина всех отрезков равна 281,7 мм и на все пропилы приходится 18,3 мм.
Вначале статистическое моделирование было выполнено по двум выборкам из 65 и 60 пар значений длины остатков и от
Таблица 3. Отрезки после отпиливания от стандартного образца
|
№ п/п |
Длина отрезка, мм |
Время УЗК (по повторам), мкс |
|||||
|
теорет. |
фактич. |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0 |
0 |
- |
- |
- |
- |
- |
|
2 |
50 |
49,8 |
33,3 |
33,3 |
33,4 |
33,2 |
33,3 |
|
3 |
50 |
49,2 |
33,0 |
33,1 |
33,2 |
33,1 |
33,1 |
|
4 |
40 |
39,1 |
30,8 |
30,9 |
30,8 |
30,9 |
30,8 |
|
5 |
40 |
39,5 |
31,0 |
30,9 |
31,0 |
30,9 |
31,0 |
|
6 |
20 |
19,0 |
27,2 |
27,2 |
27,3 |
27,1 |
27,2 |
|
7 |
20 |
19,2 |
28,0 |
28,1 |
28,0 |
28,1 |
28,0 |
|
8 |
20 |
20,3 |
27,6 |
27,6 |
27,6 |
27,5 |
27,7 |
|
9 |
20 |
18,5 |
27,2 |
27,2 |
27,3 |
27,2 |
27,3 |
|
10 |
10 |
9,6 |
25,9 |
25,9 |
25,8 |
25,8 |
25,9 |
|
11 |
10 |
9,1 |
25,6 |
25,7 |
25,6 |
25,7 |
25,8 |
|
12 |
10 |
8,4 |
25,4 |
25,5 |
25,5 |
25,5 |
25,5 |
|
13 |
5 |
6,0 |
24,0 |
24,0 |
24,0 |
24,0 |
24,0 |
резков по отношению к времени УЗК. Затем обе выборки были объединены в одну с общим количеством 125 наблюдений. Оказалось, что погрешности измерения длины в ±0,05 мм (цена деления по [1] в 0,1 мм) и отсчета времени УЗК на приборе «Пульсар-1.0» в ±0,05 мкс (цена деления 0,1 микросекунды) вполне позволяют уловить новый физический эффект.
Это - биотехническое возбуждение омертвевших клеток древесины при акустическом резонансе и росте потерь времени на малых длинах образцов. Иначе говоря, мицеллы, как гирлянды из клеток древесины, начинают поглощать внешнюю энергию ультразвука, увеличивая время прохождения УЗК.
Этот новый физико-акустический эффект можно будет применять при изучении клеточных структур древесины, например, по годичным слоям.
Такая высокая точность при выявлении статистических закономерностей изменения акустических показателей в зависимости от длины озвучиваемого образца от 5 до 300 мм (см. данные табл. 2 и табл. 3) достигается, прежде всего, отказом от классической статистики и от параметра «среднее арифметическое значение». Все наблюдения, без их группировки и последующего усреднения, учитываются при моделировании в программной среде CurveExpert-1.38 или же другой более новой версии CurveExpert-1.40.
Табличная модель, состоящая из двух статистических выборок, затем объединенных вместе для статистического моделирования идентификацией биотехнического закона
Таблица 4. Табличная модель с вычетом времени на конусные насадки 15,6 мкс, акустическая константа, кг/м3
|
№ п/п |
Остатки после отрезания от стандартного образца |
Отрезки после отрезания от стандартного образца |
||||||
|
Длина остатка L, мм |
Время УЗК, t, мкс |
Скорость УЗК, м/с |
Акустич. константа, м4/(кг с) |
Длина отрезка, мм |
Время УЗК, мкс |
Скорость УЗК, м/с |
Акустич. константа, м4/(кг с) |
|
|
1 |
300.1 |
62.7 |
4786.28 |
11.43 |
49.8 |
17.7 |
2813.56 |
6.72 |
|
2 |
249.2 |
53.5 |
4657.94 |
11.12 |
49.2 |
17.4 |
2827.59 |
6.75 |
|
3 |
198.9 |
45.0 |
4420.00 |
10.55 |
39.1 |
15.2 |
2572.37 |
6.14 |
|
4 |
159.2 |
38.7 |
4113.70 |
9.82 |
39.5 |
15.4 |
2564.94 |
6.12 |
|
5 |
118.9 |
33.4 |
3559.88 |
8.50 |
19.0 |
11.6 |
1637.93 |
3.91 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
56 |
159.2 |
38.6 |
4124.35 |
9.85 |
18.5 |
11.7 |
1581.20 |
3.78 |
|
57 |
118.9 |
33.4 |
3559.88 |
8.50 |
9.6 |
10.3 |
932.04 |
2.23 |
|
58 |
98.7 |
30.9 |
3194.18 |
7.63 |
9.1 |
10.2 |
892.16 |
2.13 |
|
59 |
80.3 |
27.4 |
2930.66 |
7.00 |
8.4 |
9.9 |
848.49 |
2.03 |
|
60 |
59.3 |
18.9 |
3137.57 |
7.49 |
6.0 |
8.4 |
714.29 |
1.71 |
|
61 |
40.4 |
14.9 |
2711.41 |
6.47 |
|
|
|
|
|
62 |
30.0 |
13.3 |
2255.64 |
5.39 |
|
|
|
|
|
63 |
20.2 |
11.7 |
1726.50 |
4.12 |
|
|
|
|
|
64 |
10.9 |
10.2 |
1068.63 |
2.55 |
|
|
|
|
|
65 |
4.3 |
8.9 |
483.15 |
1.15 |
|
|
|
|
проф. П.М. Мазуркина, фрагментарно приведена в данных таблицы 4.
Объясняющей переменной становится длина L остатка или отрезка от стандартного образца по его длине, то есть вдоль волокон. Показателями были приняты следующий ряд зависимых факторов:
- время прохождения УЗК t´ без учета затрат на преодоление конусных насадок;
- время прохождения УЗК t через конусные
- насадки на датчиках с вычетом на преодоление конусных насадок в 15,6 мкс, то есть при t=t´-15,6 мкс;
- скорость ультразвука Ň как отношение пути L ко времени УЗК t на прохождение образца древесины вдоль волокон (без конусных насадок) при C=L/t;
- акустическая константа K как отношение скорости УЗК C к постоянной для всего
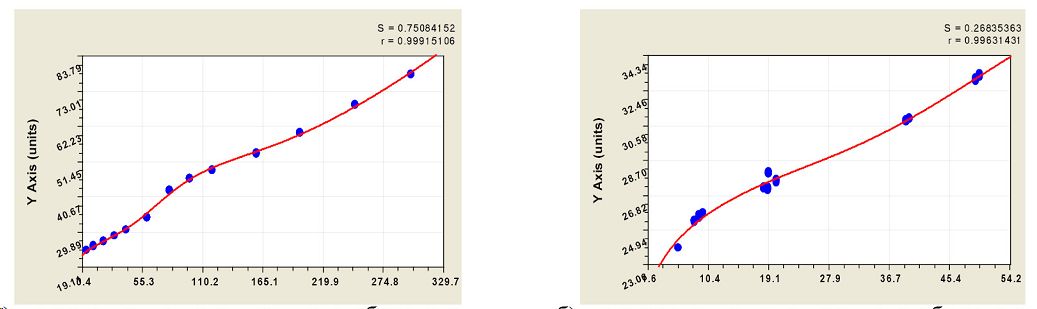
Рис 2. Графики изменения времени УЗК от длины остатков (а) или отрезков (б) от стандартного образца
стандартного образца плотности ř древесины ели, то есть K=C/ř.
Время УЗК без учета насадок. Вначале для остатков от стандартного образца ели после отпиливания была получена статистическая модель, содержащая две составляющие: во-первых, закон экспоненциального роста показателя (классический общеизвестный в различных отраслях наук закон); во-вторых, закон стрессового возбуждения показателя по биотехническому закону П.М. Мазуркина по формуле
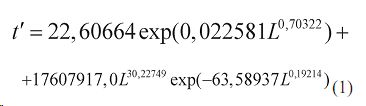
(1) Аналогичная двухчленная модель получилась и по отрезкам от стандартного образца в виде уравнения (рис. 2)
![]()
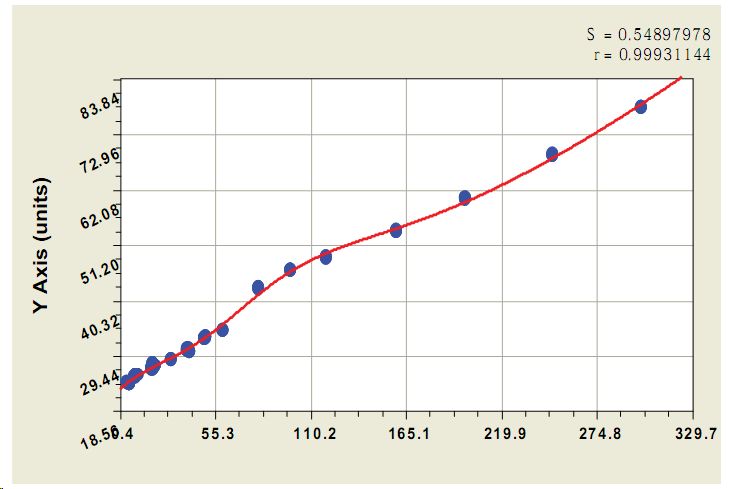
Рис. 3. График изменения времени УЗК от длины остатков и отрезков от стандартного образца
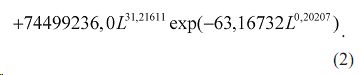 .
.
Из графика на рисунке 2б четко видно, что физико-акустический эффект наблюдается на длинах образцов до 30 мм. Второй эффект заметен на рис. 2а на участке 50-160 мм. Если объединить эти две выборки, то указанные эффекты суммируются (рис. 3), и была получена закономерность вида
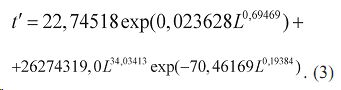
Совместное моделирование двух выборок дает больший коэффициент корреляции 0,9993. Высокая адекватность модели (3) позволяет рекомендовать способ производству.
Данный способ измерения без учета потерь времени на конусные насадки удобен для производственных испытаний, так как не требует сложной тарировки и учитывает любую насадку к датчикам заводского из
Таблица 5. Амплитудно-частотная характеристика времени УЗК без учета насадок по модели (4)
|
№ i |
Амплитуда колебания, |
Полупериод и сдвиг колебания, сутки |
Коэфф. коррел. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
22.82538 |
0 |
-0.023788 |
0.69333 |
0 |
0 |
0 |
0 |
0.9997 |
|
2 |
19768845 |
34.035814 |
70.47594 |
0.19358 |
0 |
0 |
0 |
0 |
|
|
3 |
3.73412е-5 |
2.58880 |
0.0074282 |
1.13226 |
52.31587 |
-8.20398е-5 |
2.020736 |
-0.87328 |
|
|
4 |
1.034288е14 |
8.77951 |
0.0022430 |
1.78691 |
4.71272 |
0.0030985 |
1.52993 |
-4.17294 |
0.7015 |
|
5 |
-1.87766 |
1.41605 |
0.67466 |
0.90159 |
4.59244 |
-0.082387 |
1.020982 |
-1.40870 |
0.7211 |
|
6 |
-5.94248e47 |
46.13404 |
1.59928 |
0 |
12.29466 |
-0.047133 |
0 |
0.83717 |
0.4777 |
|
7 |
1.28753e-9 |
8.58090 |
0.065134 |
1.53320 |
0.60342 |
0.011219 |
0.99630 |
5.86392 |
0.4934 |
|
8 |
-0.00073169 |
1.88613 |
0.059389 |
0.99948 |
4.66364 |
-0.020632 |
1.000041 |
-1.14217 |
0.2573 |
|
9 |
-1.19691e22 |
20.64130 |
0.67395 |
1.004236 |
0.88453 |
0.0014326 |
1.073223 |
1.37285 |
0.3033 |
|
10 |
4.010086e-6 |
3.74373 |
0.16422 |
0.84697 |
2.31313 |
-0.0074084 |
0.99351 |
-3.75828 |
0.2276 |
|
11 |
-8.21272e24 |
24.51166 |
0.86489 |
1.059427 |
0.56528 |
0.00076800 |
0.58586 |
-2.96700 |
0.8938 |
|
12 |
2.049647e15 |
7.25842 |
0.037522 |
1.001051 |
118.6568 |
-0.094623 |
1.0022255 |
1.62841 |
0.2344 |
|
13 |
0.00020650 |
2.34557 |
0.087700 |
1.027862 |
1.084533 |
-0.00069537 |
0.91315 |
-1.78349 |
0.2033 |
|
14 |
-3.11587e-8 |
6.54707 |
0.29700 |
0.99424 |
17.64968 |
-0.053551 |
1.085005 |
-4.061085 |
0.09653 |
|
15 |
-4.90158e20 |
14.52519 |
0.26842 |
1.053654 |
0 |
0 |
0 |
6.15580 |
0.1097 |
готовления как общую систематическую ошибку.
Общая закономерность. К двум составляющим уравнения три удалось дополнить еще 14 волновых уравнения, которые имеют устойчивая закономерность вида
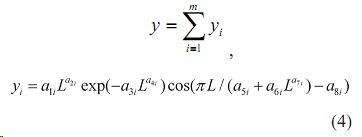
где y - изучаемый показатель, в данном случае время t´, мкс; i - номер составляющей (табл. 5); m - общее количество членов модели, в данном случае m=15; a1 ...a8- параметры обобщенной модели типа (4), характеризующие амплитудно-частотную характеристику физико-акустических эффектов клеточной структуры древесины ели.
Три составляющие по данным таблицы 5 дают адекватность модели (4) в виде коэффициента корреляции 0,9997. Это значение мало отличается от графика на рисунке 3, равное 0,9993. Однако тот факт, что четвертая составляющая к остаткам от предыдущих уравнений дает коэффициент корреляции 0,7015, заставляет задуматься над микроскопическими эффектами, кото
Таблица 6. Амплитудно-частотная характеристика времени УЗК с учетом насадок по модели (4)
|
№ i |
Амплитуда колебания, |
Полупериод и сдвиг колебания, сутки |
Коэфф. коррел. |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
6.53421 |
0 |
-0.14082 |
0.48666 |
0 |
0 |
0 |
0 |
0.9997 |
|
2 |
22295797 |
30.58921 |
64.83384 |
0.19070 |
0 |
0 |
0 |
0 |
|
|
3 |
1.57733e-5 |
2.79340 |
0.0061413 |
1.17348 |
56.057812 |
-0.00022864 |
1.92455 |
-1.21729 |
|
|
4 |
2.92142e-13 |
7.97237 |
0.0027537 |
1.73494 |
5.25385 |
0.0013336 |
1.69990 |
-11.83650 |
0.7385 |
|
5 |
-2.38479 |
0.97323 |
0.70238 |
0.79380 |
4.37320 |
-0.069438 |
1.044073 |
-1.17709 |
0.7063 |
|
6 |
1.029661e-41 |
39.17801 |
1.058775 |
1.046353 |
9.33099 |
0.85633 |
0 |
0 |
0.4058 |
|
7 |
3.64565e-24 |
30.028112 |
2.05200 |
0.95970 |
0.39063 |
0.0044756 |
1.032066 |
5.85337 |
0.8524 |
|
8 |
1.16129e-75 |
52.080141 |
0.24294 |
1.25255 |
0 |
0 |
0 |
0 |
0.3876 |
|
9 |
1.0255e12 |
10.0059 |
0.27650 |
1 |
0.14037 |
-1.88861e-8 |
0.99999 |
-2.44301 |
0.5247 |
|
10 |
0.011600 |
0 |
-0.017841 |
0.80076 |
224.066 |
-0.66052 |
0.83740 |
-2.15814 |
0.2560 |
|
11 |
-0.0087243 |
1.57638 |
0.39164 |
0.71933 |
1.012932 |
0.0066021 |
0.95836 |
-0.67983 |
0.2908 |
|
12 |
-2.91504e-9 |
15.73953 |
1.93126 |
1.008407 |
0 |
0 |
0 |
0 |
0.2274 |
|
13 |
-2.083647e11 |
13.31683 |
0.90614 |
1.0000002 |
0.24516 |
-4.20375e-8 |
0 |
3.0032368 |
0.2743 |
|
14 |
-3.56927e-14 |
16.85901 |
1.11588 |
1.015623 |
12.037233 |
-0.0022258 |
1.92291 |
-1.095352 |
0.1122 |
|
15 |
-6.35976e-9 |
7.18120 |
0.30971 |
1.00000 |
0.53547 |
5.27676e-9 |
0 |
-2.17117 |
0.1438 |
|
16 |
1.85304e-10 |
5.47115 |
0.071391 |
0.96795 |
29.23144 |
0.057384 |
1.057384 |
6.043205 |
0.1786 |
рые относятся к изучению свойств клеток древесины.
Время с учетом конусных насадок.
По формуле (4) была получена матрица параметров модели (табл. 6) для времени t без учета затрат на конусные насадки.
Сравнение показывает, что по сравнение с предыдущим анализом, количество составляющих модели типа (4) выросло на одно волновое возмущение и стало m=16. исключение систематической ошибки улучшило идентификацию микроэффектов.
Таблица 7. Амплитудно-частотная характеристика скорости УЗК с учетом насадок по модели (4)
|
№ i |
Амплитуда колебания |
Полупериод и сдвиг колебания, сутки |
Коэфф. коррел. |
||||||
|
a 1i |
a 2i |
a 3i |
a 4i |
a 5i |
a 6i |
a 7i |
a 8i |
||
|
1* |
5445.1958 |
0 |
0.040585 |
0.69796 |
0 |
0 |
0 |
0 |
0.9992 |
|
2 |
-96.85926 |
0.39638 |
7.40969e-6 |
2.51259 |
59.83265 |
1.79820e-5 |
2.41915 |
-0.99012 |
|
|
3 |
-6.57157e-32 |
24.39622 |
0.38061 |
1.0014617 |
14.80385 |
6.040138e-5 |
2.13334 |
3.21154 |
0.7561 |
|
4 |
4.54489e-8 |
8.87410 |
0.28669 |
1.011090 |
0.94838 |
0.00023576 |
1.30817 |
4.10071 |
0.6511 |
|
5 |
-0.44594 |
0.82021 |
0 |
0 |
66.12885 |
8.038424e-5 |
2.0019898 |
0.35090 |
0.5255 |
|
6 |
57110.018 |
0 |
4.31982 |
0.28031 |
3.83790 |
-0.44176 |
0.29359 |
-0.013770 |
0.6109 |
|
7 |
0.00077651 |
6.014481 |
0.39135 |
0 |
0.25160 |
-1.023268 |
0 |
0 |
0.4533 |
|
8 |
-0.28322 |
35.01571 |
37.19131 |
0.33070 |
0.51378 |
0.40188 |
0 |
0 |
0.5585 |
|
9 |
67.32605 |
11.35348 |
13.65159 |
0.31705 |
1.78119 |
-0.41751 |
0.13649 |
-8.036395 |
0.5915 |
|
10 |
-6.71917e-10 |
5.99998 |
0.0025782 |
1.5140 |
2.014035 |
1.35871 |
0 |
0 |
0.4534 |
|
11 |
-2.51050e-19 |
25.85620 |
1.59860 |
1.000001 |
0.29642 |
1.88173e-7 |
0 |
2.56746 |
0.5592 |
|
12 |
2.52703e-5 |
3.83886 |
0.048079 |
0 |
6.69438 |
-0.011641 |
1.0095905 |
-4.67595 |
0.2961 |
Примечание. * По структуре формулы (5).
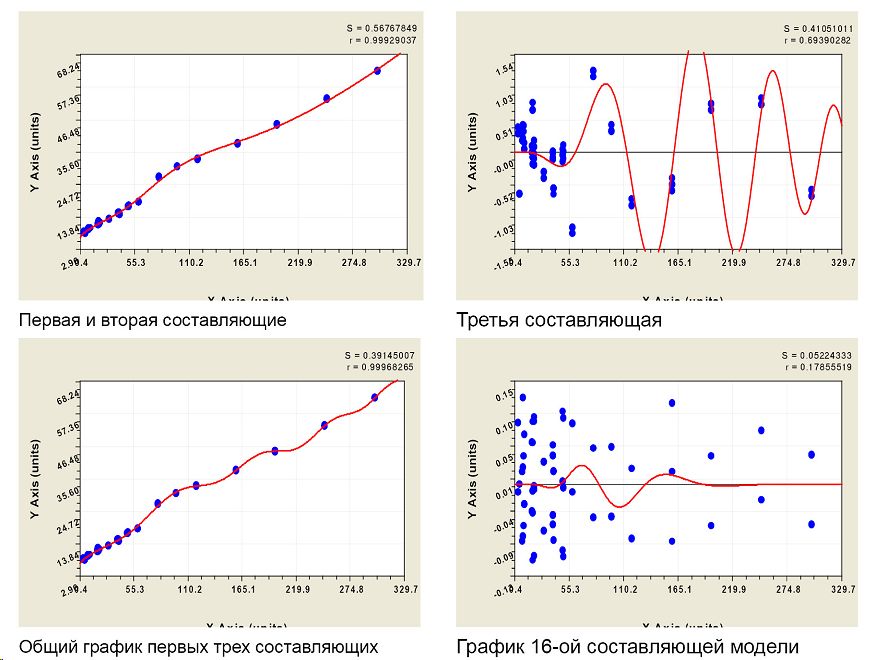
На рисунке 4 приведены графики нескольких составляющих всей модели.
Скорость ультразвука. Погрешности измерений равны ± 0,05 мм по длине и ± 0,05 мкс по времени. Поэтому скорость УЗК приводится с двумя знаками после запятой.
Первая составляющая имеет другую конструкцию (рис. 5) в виде формулы
C = 4991,333(1 - exp(-0,048136L 0,71131 ) (5)
Параметры модели (5) таковы, что значение 4991,3 м/с показывает предельную скорость на бесконечно длинном образце из древесины ели. Матрица дана в таблице 7.
Заметно снизилось количество составляющих, потому что показатель скорости УЗК становится инвариантным по отношению к различным длинам образцов. Тогда можно определить условия применимости того или иного показателя: время учитывается при постоянной длине пути прохождения ультразвука, а скорость ультразвука применятся при разных расстояниях озвучивания (рис. 5).
Из данных таблицы 7 видно, что каждая волновая составляющая имеет тесноту связи выше слабой, то больше по коэффициенту корреляции 0,3 (кроме 12-ой).
Плотность древесины [3] переменная физическая величина вдоль ствола у растущего дерева. Поэтому можно вычислять акустическую константу и/или акустическое сопротивление [2, с.16] по разным участкам и точкам ствола растущего лесного дерева. В статье приводим только анализ показателя «акустическая константа».
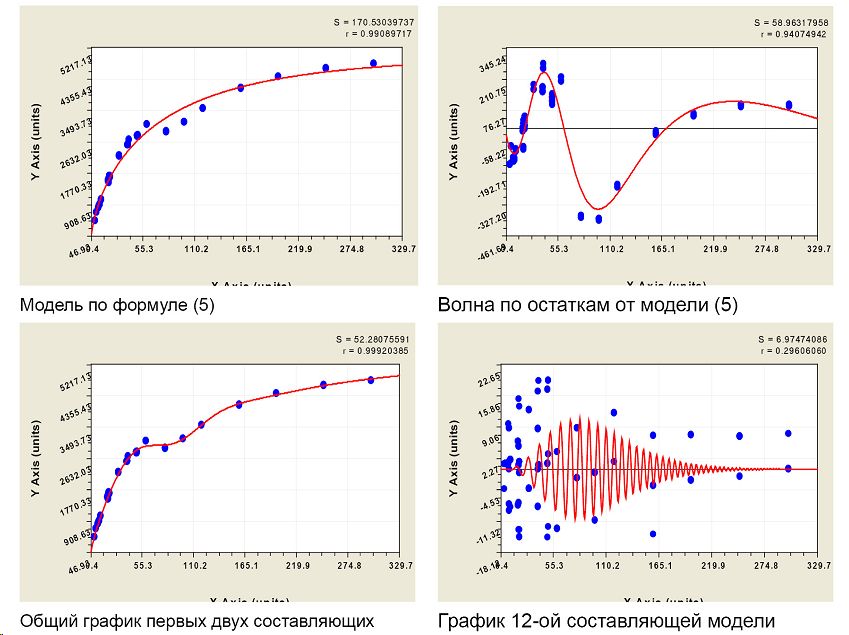
Таблица 8. Плотность древесины по отрезкам от стандартного образца
|
№ п/п |
Длина, мм |
Ширина, мм |
Толщина, мм |
Объем, мм3 |
Масса, г |
Плотность, кг/м3 |
|
1 |
49,6 |
20,1 |
20,2 |
20138,59 |
8,463 |
420,2 |
|
2 |
49,3 |
20,3 |
20,2 |
20215,96 |
8,324 |
411,8 |
|
3 |
39,1 |
20,1 |
20,0 |
15718,20 |
6,610 |
420,5 |
|
4 |
39,4 |
20,3 |
20,0 |
15996,40 |
6,666 |
416,7 |
|
5 |
18,9 |
20,4 |
20,1 |
7749,76 |
3,224 |
416,0 |
|
6 |
19,0 |
20,6 |
19,9 |
7788,86 |
3,312 |
425,2 |
|
7 |
19,5 |
20,1 |
20,0 |
7839,00 |
3,362 |
428,9 |
|
8 |
18,2 |
20,0 |
20,1 |
7316,40 |
3,022 |
413,0 |
|
9 |
9,9 |
19,9 |
20,1 |
3959,90 |
1,544 |
389,9 |
|
10 |
10,3 |
20,0 |
19,9 |
4099,40 |
1,385 |
337,9 |
|
11 |
8,4 |
19,8 |
19,8 |
3293,14 |
1,318 |
400,2 |
|
12 |
5,1 |
20,0 |
19,7 |
2009,40 |
0,876 |
436,0 |
|
13 |
4,4 |
19,9 |
19,3 |
1689,91 |
0,706 |
417,8 |
|
|
|
|
|
|
Ʃ |
4606,3 |
|
|
|
|
|
|
среднее |
418,8 |
Этот производный показатель вычисляется как отношение скорости ультразвука к плотности древесины, которая ля стандартного образца нами принимается постоянной величиной, равной 418,8 кг/м3 (табл. 8).
Заметно, что некоторые отрезки имеют малую плотность, и эти данные мы исключили из расчета среднеарифметической плотности. В будущем можно учитывать денсиметрическое распределение по древесине на разных местах ствола лесного дерева.
Различие показателя плотности в разных точках даже у стандартного образца определяется наличием пустот и смоляных кармашков в древесине. Поэтому даже на микро уровне измерений в будущем нужно учитывать различие в плотности, а это означает различие и в показателях акустической
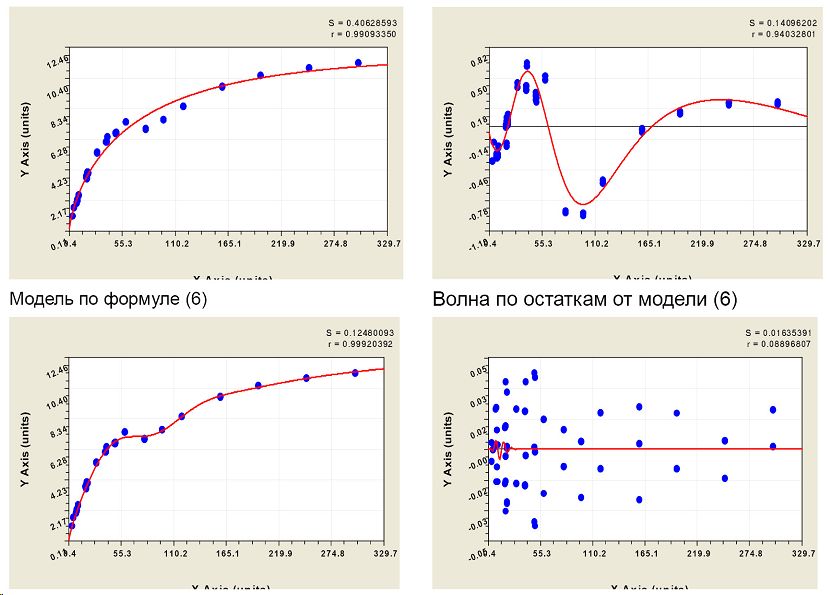
Рис. 5. Графики скорости УЗК С от длины образца ,с вычетом времени на конусные насадки
константы и акустического сопротивления древесины. Известно также, что плотность резко разнится в каждом годичном слое по поздней и ранней древесине (почти в два раза).
Акустическая константа. Из-за принятого постоянства плотности первая составляющая имеет конструкцию (рис. 6), как и у скорости ультразвука, в виде формулы
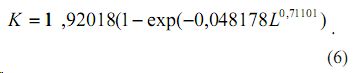
Параметры модели (6) таковы, что значение 11,92 < [K] = 13 м4/(кг с) и показывает предельную акустическую константу на бесконечно длинном образце из древесины ели, которая меньше нормативного значения для отнесения образца к резонансной древесине. При этом получилось 16 составляющих и этот факт указывает на то, что, при точном измерении плотности древесины в точках озвучивания, можно в будущем проводить тонкие физико-акустические исследования древесины.
С учетом волновой составляющей, то есть по формуле первых двух составляющих,
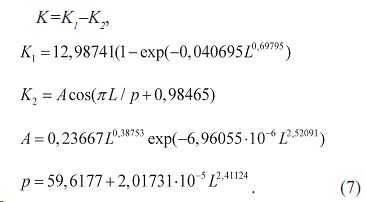
расчетное значение акустической константы достигло 12,99. А это уже близко к резонансной древесине, поэтому нужно испытывать детали музыкальных инструментов для установления нормативного значения допустимой акустической константы. Приведенные результаты исследования масштабного фактора позволяют расширить функциональные возможности комплексного исследования древесины [4], причем неразрушающими методами непосредственно на растущем дереве в условиях леса.
Список литературы
- ГОСТ 16483.31-74. Резонансный метод определения модулей упругости и сдвига и декремента колебаний. - М.: Изд-во Стандартов, 1974. - 8 с.
- Колесникова, А.А. Исследование свойств древесины по кернам / А.А. Колесникова. - Йошкар-Ола: МаргТУ, 2002. -178 с.
- Мазуркин, П.М. Изменение плотности древесины по высоте дерева / П.М. Мазуркин, р.И. Винокурова, Е.В. Тарасенко, В.Ю. Осипова // Лесной журнал. - 2000. -№3. - С. 102-108.
- Мазуркин, П.М. Перспективы комплексного исследования древесины / П.М. Мазуркин // Деревообрабатывающая промышленность. - 1997. - №4. - С. 27-29.
- Пат. 2334984 российская Федерация, МПК G01N33/46 (2006.01). Способ ультразвукового испытания поленьев резонансной древесины / Мазуркин П.М., Темнова Е.Б. (РФ); заявитель и патентообладатель Марийск. гос. тех. ун-т. - №2006126506/12; заявл. 20.07.2006; опубл. 27.09.2008.
- Темнова, Е.Б. Применение ультразвука в определении резонансных свойств древесины поленьев / Е.Б. Темнова // Успехи современного естествознания. - 2009. -№ 8. - С. 8-15.
- Темнова, Е.Б. Время распространения ультразвуковых колебаний через конусные насадки в эталонном образце из оргстекла / Е.Б. Темнова, П.М. Мазуркин // Казанская наука. - № 1. - 2010. - Казань: Изд-во Казанский Издательский Дом, 2010. - С.23-28.
Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603МОН РФ/
Библиографическая ссылка
П.М. Мазуркин, Е. Б. Темнова МАСШТАБНЫЙ ФАКТОР УЛЬТРАЗВУКОВЫХ ИСПЫТАНИЙ ДРЕВЕСИНЫ ЕЛИ ВДОЛЬ ВОЛОКОН НА СТАНДАРТНОМ ОБРАЗЦЕ // Современные наукоемкие технологии. 2010. № 6. С. 57-68;URL: https://top-technologies.ru/ru/article/view?id=24962 (дата обращения: 05.03.2026).



