Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

П.М. Мазуркин

Классическое лесоведение зиждется на индивидуальном подходе к каждому растущему в лесу дереву и поэтому в европе получила широкое распространение дендрометрия. исходя из дендрометрических представлений о древесном стволе нам удалось сформировать теоретические представления о возрастной структуре любого типа древостоя. За объект был принят разновозрастный сосняк из Сибири на пробной площади № 1963–4. Первичный материал по всем модельным деревьям из этого древостоя был предоставлен проф. П.М. Верхуновым. По таксационным описаниям в древостое сосны обыкновенной находились 202 модельных дерева. Тщательные измерения и анализ каждого ствола сосны по всему разновозрастному сосняку позволили провести эвристико-статистическое моделирование идентификацией устойчивых законов.

Статья в формате PDF

2827 KB

Классическое лесоведение зиждется на индивидуальном подходе к каждому растущему в лесу дереву [1, 10] и поэтому в Европе получила широкое распространение дендрометрия [7, 8]. Исходя из дендрометрических представлений о древесном стволе [6] нам удалось сформировать теоретические представления о возрастной структуре любого типа древостоя.

Пришлось отказаться от группировки деревьев по классу возраста. Как известно [4,5], одновозрастными считаются древостои, содержащие в своем составе деревья в одном классе возраста, то есть для сосняка возраст всех деревьев различима в пределах 20 лет.

Но такого 20-летнего цикла в природе не существует, поэтому естественным измерителем является только цикл вращения Земли вокруг Солнца, то есть один год. Одновозрастным следует считать древостой с деревьями, различающимися по возрасту с погрешностью ±0,5 лет.

За объект исследования был принят разновозрастный сосняк из Сибири [2, 3] на пробной площади № 1963-4. Первичный материал по всем модельным деревьям из этого древостоя был предоставлен нам проф. П.М. Верхуновым около 10 лет назад, но сам он не успел прочитать эту статью. По таксационным описаниям из монографий [2, 3] в древостое сосны обыкновенной находились 202 модельных дерева. Тщательные измерения и анализ каждого ствола сосны, выполненные экспедицией П.М. Верхунова в 1963 году по всему разновозрастному сосняку, позволили нам провести эвристикостатистическое моделирование данных экспериментов с применением идентификации устойчивых законов [9].

Рис. 1. Распределение модельных деревьев сосны (показаны точками) и график тренда (1) с коэффициентом корреляции 0,7927 (за метны кластеры по поколениям модельных деревьев сосны))

Как пример, на рис. 1 показан график изменения диаметра в коре Dк _1,3  в зависимости  от возраста А (в момент проведения измерений) по формуле

Далее в статье рассмотрим только фактор возраста А, который был определен одномоментными измерениями после валки и раскряжевки ствола модельных деревьев, как это было выполнено в 1963 году. В будущем измерения возраста можно будет проводить с использованием наших изобретений, причем в динамике развития и роста учетных деревьев. В частности, испытания растущих деревьев выполняются с применением частично разрушающих (методы керна) и не разрушающих (методы ультразвуковой диагностики) способов.

Тогда в дендроэкологическом мониторинге территории свойствами растущих деревьев первым фактором становится возраст дерева (рис. 2).

Для составления схемы возрастной структуры всех деревьев в одном древостое [2, 3]

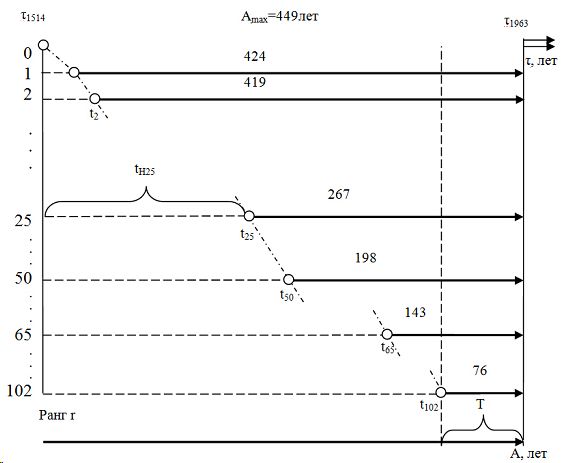
Рис. 2. Дендрохронологические шкалы разновозрастного сосняка № 1963-4

необходимы следующие шкалы времени:  t - хронологическое время (с рождества Христово), лет; t₁₉₆₃ — время проведения дендрометрических измерений в 1963 году и начало шкалы времени последующих преобразований срезанного дерева; A - возраст 202 деревьев сосны в момент проведения измерений, лет; A_max — возраст самого старого в древостое дерева сосны, в нашем примере A_max=449 лет для разновозрастного сосняка Сибири; A_min — возраст самого молодого дерева в популяции, в примере 76 лет; t₁₅₁₄ — начало возникновения, развития и роста самого старого дерева в 1963 — 449 = 1514 г., лет; t₁₈₈₇ — начало возникновения, развития и роста самой молодой особи сосны в 1963 — 76 = 1887 г., лет; T — период жизни древостоя в полном составе с 1887 по 1963 гг., лет; t — биологическое время каждого дерева сосны, причем 0≤t≤A, лет; t_i — время начала жизни деревьев в сравнении со старым деревом сосны, поэтому для нашего примера t_i =A_max – A, лет; T_c=A_max– A_min — период сукцессии разновозрастного сосняка, лет.

Для статистического анализа вводятся параметры древостоя: N — общее количество деревьев в древостое, шт.; N_A — количество деревьев одного возраста в древостое, шт.

Таблица 1. Фрагмент табличной модели разновозрастного сосняка по возрастной структуре

Схема на рисунке 2 позволяет составить не только возрастную структуру, но и рассмотреть ход роста каждого дерева в древостое в процессе его становления (сукцессии) сменой деревьев (но неизвестны заменяемые особи). При этом очевидно, что древостой с деревьями одного возраста, то есть лесное насаждение, по всем своим особям древесных растений получает простое математическое условие A_max=A_min=A=_const.

Фрагмент табличной модели возрастной структуры приведен в таблице 1.

Для удобства шкалы возраст A всех N=202 деревьев был вначале ранжирован по убыва

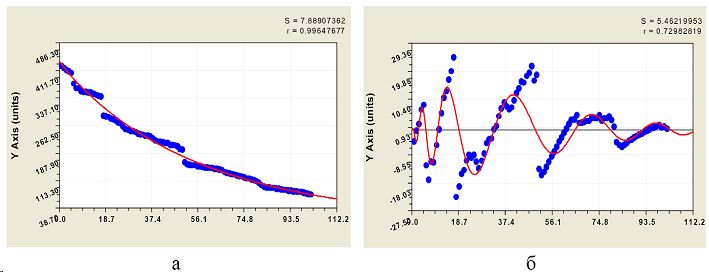
Рис. 2. Графики структурной динамики разновозрастного сосняка (здесь и далее абсцисса — ранг возраста, ордината — возраст сосен): а — тренд возрастной структуры; б — волновая кризисная составляющая модели

нию значений. Одновозрастные деревья сосны получили один и тот же ранг r возраста. Затем по формуле t _i=A_max–A вычисляли время начала жизни каждого модельного дерева. А в последнем столбце табл. 1 определяли количество одновозрастных деревьев NA сосны.

Возрасты деревьев. Тренд распределения возраста деревьев изменяется по закону экспоненциальной гибели (спада) в виде уравнения (рис. 2а)

A = 437,1551exp(−0,021735r ^0,94944 ) . (1)

Ранг возраста — это группировка с интервалом в единицу хронологического времени (год). При этом ранг повторяет распределение возраста A деревьев в древостое, но без промежутков времени для «нулевых» деревьев. Таким образом, можно представить теоретически древостой численностью N особей, у которого каждое дерево взрастало в очередном году хронологического времени t. Тогда теоретический образ разновозрастного сосняка включает 202 сосны на шкале в 202 ранга. Фактически, из-за низовых пожаров и других причин, сосняк пополнялся новыми деревьями не каждый год.

Поэтому график тренда с корреляцией 0,9965 и линия в виде точек на рисунке 1а около него показывают наличие волнового возмущения популяции.

По остаткам от тренда (1) была получена волновая функция, показанная на рис. 2б и имеющая коэффициент корреляции 0,7298.

После объединения в программной среде CurveExpert-1.3 обеих составляющих (частей модели) была получена (рис. 3а) закономерность вида

A = 433,8273exp(−0,020298r ^0,96307 ) + Αcos(pr /Ρ − 0,96307) (2)

Α = −2,59236r ^0,88008 exp(−0,042115r) ,

Ρ =1,81492 + 0,088307r ^1,22836 exp(−0,011167r)

где A — половина амплитуды кризисного возмущения древостоя, лет, P — половина периода колебательной адаптации древостоя, ранг.

На рисунке 3б видны импульсные функции влияния, по крайней мере, двух лесных пожаров. После моделирования до погрешности измерений ±0,5 года получили всего 40 составляющих, из которых 39 показывают

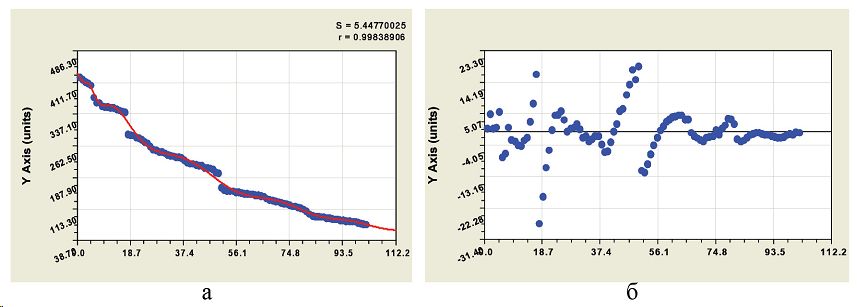
Рис. 3. Графики структурной динамики возраста сосняка по двухчастной модели: а — график модели (2) из двух составляющих; б — остатки после статистической модели (2)

волновую динамику адаптации разновозрастного сосняка по возрастной структуре.

Возраст древостоя. Этот параметр популяции лесных деревьев может иметь различные значения. От среднеарифметического значения, по возможности, нужно отказываться, так как различные распределения возраста и других параметров деревьев,

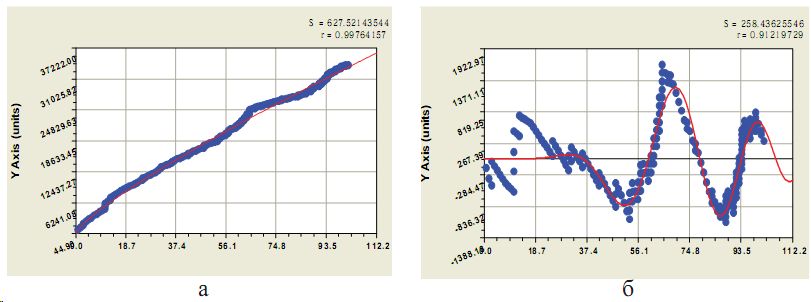
Рис. 4. Кумулятивный возраст деревьев разновозрастного сосняка Сибири: а — график тренда (3); б — график первой волновой составляющей модели

как правило, могут иметь одну и то же среднюю арифметическую, в нашем случае A=33879/202=167,7 лет.

 Сосняк Сибири характеризуется следующими параметрами возраста:

• минимальный возраст дерева A_min=76 лет; — максимальный возраст дерева в сосняке A_max=449, лет;
• размах возраста деревьев T_c=A_max– Amin=373 года;
• кумулятивный возраст древостоя равен Ʃ=33879 лет в 1963 г.

В структурной динамике кумулятивный возраст деревьев ƩA изменяется в разново-

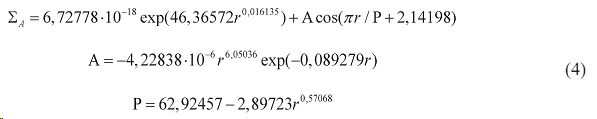
зрастном сосняке (рис. 4а) по биотехнической закономерности (3)

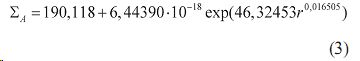
После совместной параметрической идентификации по методике [9] была получена статистическая модель в виде двухчастного уравнения

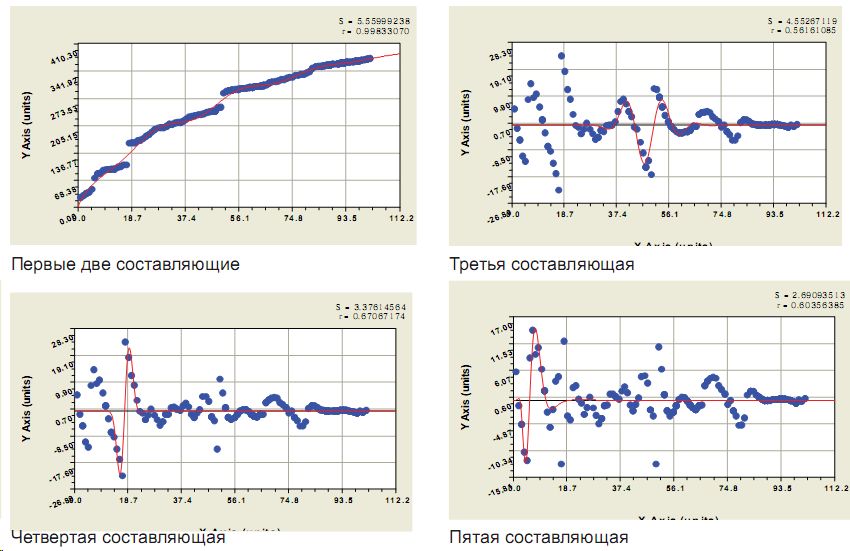
Рис. 6. Амплитудно-частотные характеристики (АЧХ) влияния трех лесных пожаров

Таким образом, амплитудно-частотная характеристика (АЧх) поведения деревьев в популяции разновозрастного сосняка сложная, причем, как и в формуле (2), волновое возмущение деревьев в древостое кризисное.

Время начала жизни деревьев. В сравнении с самым старым деревом сосны время t _i определилось (рис. 5а) биотехническим законом [6–9] вида

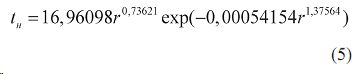(5)

Двухчастная статистическая модель имеет вид

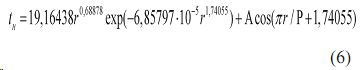(6)

Таблица 2 Параметры первых восьми составляющих ранговой модели возрастной структуры по появлению проростков сосен в разновозрастном сосняке после старой сосны

Шкала времени t _i с начала зарождения старой сосны оказалась эффективней предыдущих двух шкал времени из-за меньшего количества составляющих в готовой статистической модели.

Четче обозначились и моменты появления лесных пожаров (рис. 6).

Параметры АЧх по составляющим модели в компактной записи приведены в табл. 2 по конструкции формулы биотехнической функции [6-9]

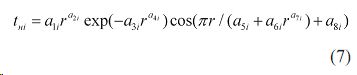(7)

где i — номер составляющей по ходу процесса идентификации, a1...a8 — параметры вейвлет-функции (7) колебательного возмущения.

Показатель времени t _i с начала жизни самой первой сосны 1514 года рождения до моментов проростков остальных сосен популяции точнее отражает сукцессию, хотя нам неизвестны заменяемые молодыми соснами виды деревьев. Через 383 года (возраст старой особи) древостой в 1887 году «наполнился» и дальше до 1963 года он жил по закону так называемого стационарного случайного процесса. Причем стационарность приближенно определяется формулой первой не волновой составляющей формулы (6) и табл. 2.

Одновозрастные деревья. Ими являются одногодки сосен. разновозрастный древостой, как это видно в последнем столбце табл. 1, имеет количество NA одновозрастных деревьев. По данным табл. 1 были выявлены биотехнические закономерности динамики численности одновозрастных сосен в зависимости от четырех влияющих переменных — ранга r, возраста A, начала проростков ti и кумуляты ƩA с коэффициентами корреляции R.

В зависимости от ранга возраста показатель N_A изменяется так:

N_A =1,11878exp(0,0010296r ^1,53303 ) ,

R = 0,4891. (8)

От возраста численность однолеток сосны распределяется по формуле

N_A =- 7339590,7exp( 1 ,44652A ^0,055009 ),

R = 0,4933 . (9)

От начала проростков показатель N_A изменялся по выражению ,

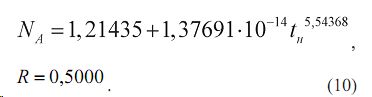
А от кумулятивного возраста деревьев A N менялась по зависимости ,

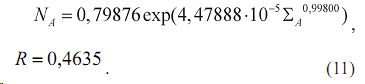
Вместо среднестатистических трендов информативными оказались закономерности максимальной продуктивности генерирования деревьев разновозрастным сосняком.

 Моделированием были получены формулы изменения (воспроизводства) одновозрастных сосен в зависимости от шкал:

 - ранга возраста (рис. 7а)

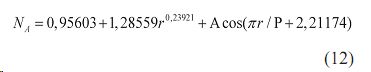
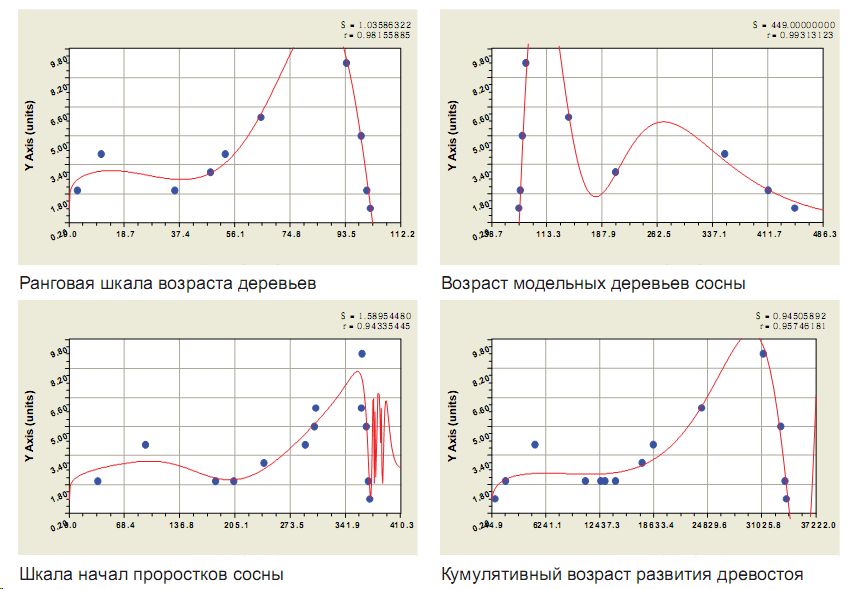
Рис. 7. АЧХ влияния дендрохронологических шкал в разновозрастном сосняке Сибири

A=0,0031651r ^1,74080,

P=78,51144– 0,00025202r ^2,49111;

 - возраста в момент рубки модельных деревьев (рис. 7б)

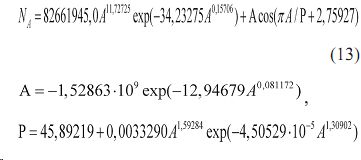(13) ,

- времени начал проростков новых сосен (рис. 7в)

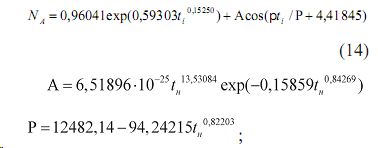
 - кумулятивного возраста нарастающего по числу деревьев сосняка

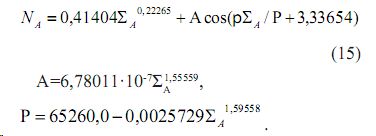
Шкала кумулятивного возраста древостоя, созданная на базе ранжированного по убыванию возраста у отдельных деревьев, оказывается наиболее действенной из рассмотренных выше четырех шкал времени. Она позволяет провести идентификацию множества вейлет-функций типа (7) до точности измерений возраста модельных деревьев на спилах-кружках, то есть до погрешности в ±0,5 года. Поэтому этот показатель есть системный параметр возрастной структуры развивающегося с 1514 по 1963 гг. сосняка. Он косвенно характеризует в каждый момент про-

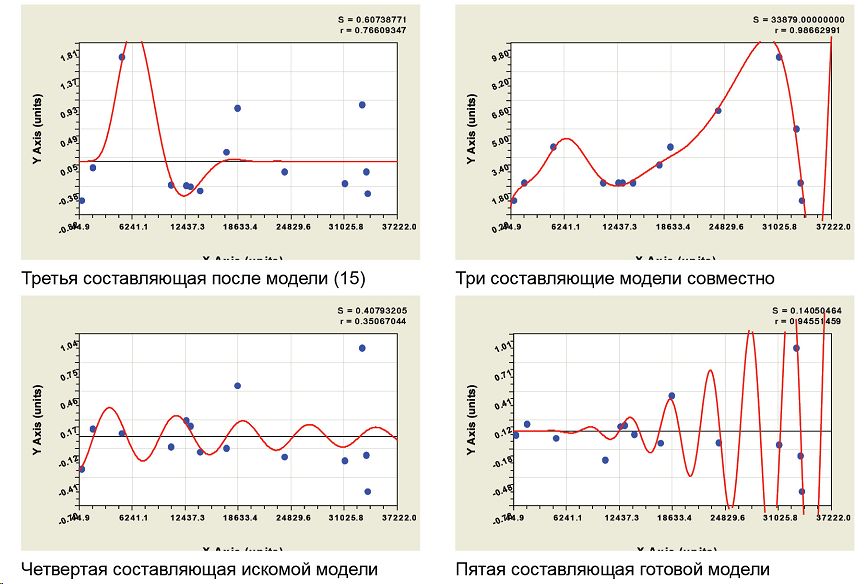
 Рис 8. АЧХ влияния кумулятивного возраста сосняка на число одновозрастных сосен

шлого времени синергетическое состояние популяции из взрослеющих сосен. Популяция в динамике биоэнергетического воздействия на среду «вытягивает» из находящихся в почве семян новые проростки. Здесь больше симбиотического содружества, чем конкуренции. Поэтому подтверждается теория лесной экологии [10] нашими моделями.

Все выявленные части модели N_A=f(Ʃ_A) приведены графически на рисунке 8, а их параметры записаны в данных таблице 3. Высокие измерительные перспективы и практические возможности поиска принципиально новых (патентоспособных) технических решений видны из высокой идентификационной адекватности пятой составляющей на рис. 8. Здесь даже на долях года (по-видимому, влияние сезонов года)

Таблица 3. Параметры составляющих модели кумулятивной возрастной структуры по появлению одновозрастных проростков сосен в разновозрастном сосняке

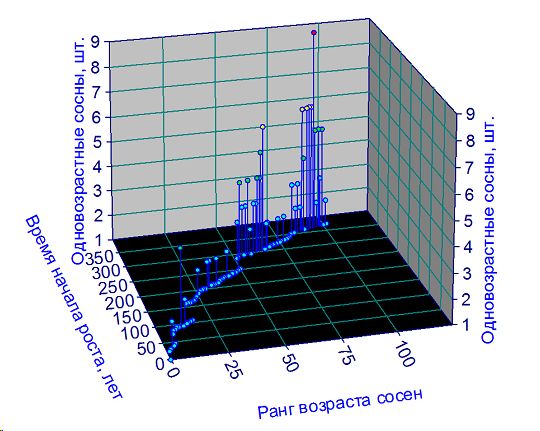
Рис. 9. Изменение численности одновозрастных сосен

коэффициент корреляции очень высокий и равен 0,9455.

Сравнение с графиками на рис. 6 показывает, что на появление импульса проростков новых сосен по третьей составляющей на рис. 8 повлияли два крупных лесных пожара по четвертой и пятой составляющим на рис. 6.

Из данных таблицы 3 по знакам параметра a8 видно, что первые четыре составляющие общей модели кумулятивной возрастной структуры древостоя начались позже 1514 года, то есть в процессе жизни самой старой в 1963 г. сосны, срубленной таксаторами в возрасте 449 лет. Хорошими познавательными возможностями обладают и предыдущие дендрохронологические шкалы. Например, совместное влияние двух шкал — ранга r возраста и времени t _i начала роста сосен — показано на рисунке 9.

До пожаров появляется в год по одному или два проростка, а после них появлялись три или четыре сосенки. Но наибольшее количество одновозрастных деревьев появилось после завершения сукцессии древостоя и его взросления. К этому моменту накопилась достаточная биоэнергетика у популяции сосен. Поэтому увеличилось число проростков, вытягиваемых биоэнергетикой всей популяции из семян.

Устойчивость разновозрастного сосняка была в течение 100 лет, до одномоментной смерти от его сводки таксаторами на модельные деревья.

Заключение. Моделирование возрастной структуры различными дендрохронологическими шкалами показало, что про динамику поведения древостоя можно узнать относительно возраста самого старого дерева. Изученный таксаторами [2, 3] разновозрастный сосняк жил два этапа: а) сукцессия с неизвестными замещенными растениями по мере наращивания популяции сосен с 1514 по 1887 гг.; б) по численности популяции сосен относительно стабильная пора жизнедеятельности деревьев с 1887 по 1963 гг.

Поколения деревьев возникли из-за лесных низовых пожаров, однако биоэнергетическая связь не прерывалась: наоборот, после пожаров возрастало количество проростков новых сосен. Поэтому к «срезу» хронологического времени в 1963 г. каждым деревом был достигнут свой биологический возраст A. распределение значений A у членов популяции определяет, как показано на рис. 1, любой известный [2, 3] таксационный показатель без разделения деревьев по поколениям.

Предложены четыре дендрохронологические шкалы, из которых в будущем наиболее информативным окажется кумулятивный возраст сообщества деревьев. Этот динамичный параметр определяет синергетические свойства сосняка, косвенно даже показывает общую биоэнергетику популяции, симбиотическим образом позволяющую как бы «вытягивать» из семян, находящихся в лесной почве внутри древостоя, новые проростки. Тем самым разновозрастный древостой гасит внутривидовую конкуренцию, обеспечивая коэволюцию как старых и средних, так и молодых лесных деревьев сосны.

Список литературы

1. Бюсген, М. Строение и жизнь наших лесных деревьев / Пер. с нем. / М. Бюсген - М.-Л.: Гослесбумиздат, 1961. - 424 с.
2. Верхунов, П.М. Закономерности строения разновозрастных сосняков / П.М. Верхунов. - Новосибирск: Наука, 1976. - 255 с.
3. Верхунов, П.М. Прирост запаса разновозрастных сосняков / П.М. Верхунов. - Новосибирск: Наука, 1979. - 254 с.
4. Верхунов, П.М. Таксация отдельных деревьев и их разнородных совокупностей: Учеб. пос. / П.М. Верхунов, М.Л. Дворецкий. - Горький: ггу, 1979. - 100 с.
5. Верхунов, П.М. Таксация прироста древесного ствола: Учеб. пос. / П.М. Верхунов, М.л. Дворецкий. - Горький: ГГУ, 1979. - 51 с.
6. Верхунов, П.М. Таксация древесного ствола лесных насаждений: учеб. пос. / П.М. Верхунов, П.М. Мазуркин. - йошкарОла: МаргТу, 1999. - 72с.
7. Мазуркин, П.М. Дендрометрия. Статистическое древоведение / П.М. Мазуркин. - учеб. пос. - Часть 1. - Йошкар-Ола: МаргТу, 2003. - 308с.
8. Мазуркин, П.М. Дендрометрия. Статистическое древоведение. / П.М. Мазуркин. - учеб. пос. - Часть 2. - Йошкар-Ола: МаргТу, 2003. - 205с.
9. Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: учеб. пос. / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МаргТу, 2006. - 292 с.
10. Спурр, С.Г. Лесная экология: Пер. с 3-го англ изд. / С.г. Спурр, Б.В. Барнес - М.: Лесн. пром-сть, 1984. - 480 с.

Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603 МОН РФ.

Библиографическая ссылка