Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Резеньков Д.Н.

Статья в формате PDF

115 KB

Для реализации вычислительного процесса с использованием ПСКВ необходимо осуществить преобразование из позиционного кода в модулярный и обратно.

Обратное преобразование из ПСКВ в позиционную систему счисления (ПСС) базируется на применении обобщенной полиадической системы (ОПС) счисления. Введение промежуточной системы счисления [1,3,4], позволяет изображать число А в виде

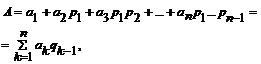(1)

где a_k - цифры в полиадической системе счисления; q_k = p_kq_k-1 - вес цифры в ОПС (смешанный базис).

Если обеспечить соответствие между основаниями ОПС и основаниями системы классов вычетов, то справедливо равенство

A = (a₁(z), a₂(z),...,a_n(z)) = [ a₁(z), a₂(z),...,a_n(z)]

На основании этого можно сделать вывод о возможности перевода кода класса вычетов в кодовую последовательность ОПС. При этом все процедуры должны осуществляться в модулярной арифметике.

Проведенный анализ основных реализаций вычислений коэффициента обобщенной полиадической системы счисления позволил выделить три основных подхода к построению нейросетевых устройств, предназначенных для выполнения этой немодульной операции.

Основу первого подхода составляют методы, базирующиеся на рекуррентном алгоритме вычисления коэффициентов [3,6], согласно которому

a_k = rest A_k(mod p_k)                      (2)

где A_k определяется по рекуррентной формуле

A_k = (A_k-1 - a_k-1) w_k-1            (3)

где A₁ = A; W_k = p_k^j - формальная обратная величина k-ого основания по j-ому основанию (j ≠ k); a^*_k-1 - набор остатков по всем модулям, номера которых выше номера   k-1; k=1...n.

При этом все операции по вычислению коэффициента a_k производятся в системе классов вычетов [2,6].

Наряду с достоинствами, такими как параллельно-конвейерная организация вычислений и достаточно высокое быстродействие, очевидны и недостатки данной реализации. Основной недостаток - значительные аппаратные затраты, что затрудняет широкое применение данного метода перевода из непозиционной системы классов вычетов в обобщенную полиадическую систему, определяемую в расширенных полях Галуа.

Сократить аппаратные затраты позволяют методы, обеспечивающие основу второго подхода к построению устройства для преобразования ПСКВ в ОПС [4,6]. Алгоритм вычисления коэффициента ОПС по данному методу позволяет минимизировать аппаратные затраты, необходимые для выполнения этой немодульной операции [5,6]. Последовательное получение коэффициентов  ОПС для заданного полинома  А (z)  по составным основаниям можно осуществить согласно выражения

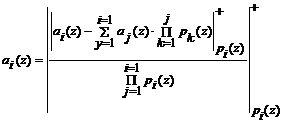               (4)

Принимая во внимание парную простоту модулей p_i(z), где , можно заключить, что схемная реализация обладает пирамидальной структурой.

Обеспечивая равную производительность с устройством функционирующем на основе (2) и (3), алгоритм определяемый выражением (4) требует в 1,5 раза меньше схемных затрат.

Основу третьего подхода к реализации процедуры вычисления коэффициентов ОПС в расширенных полях Галуа составляют методы, при которых наиболее трудоемкий этап перевода остаток - коэффициенты осуществляется путем параллельно-конвейерного вычисления коэффициентов [2,5,6]. Существование данного метода обеспечивается в условиях выполнения  КТО, согласно которой

A =  a_i (z) B_i (z) mod P(z)        (5)

где B_i  - ортогональный базис i -го основания.

Реализовав ортогональные базисы модулей ПСКВ, в виде коэффициента ОПС, получаем выражение

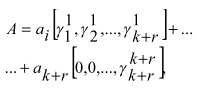       (6)

где γ_i^j - коэффициенты ОПС  j -го ортогонального базиса. Тогда, проведя умножение вычетов  на соответствующие коэффициенты  ОПС помодульно и поразрядно, при этом, учитывая превышение модуля  p_i как перенос единицы при суммировании результата, коэффициенты ОПС могут быть найдены непосредственно из выражения

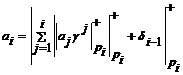,      (7)

где δ_i-1 - переполнение, полученное при суммировании по модулю p_i-1.

Одним из важнейших свойств ПСКВ, определенных в расширенных полях Галуа GF(p^v) , является отсутствие межразрядных переносов при вычислении результата по модулю p_i(z). Это позволяет свести операцию итеративного получения коэффициентов обобщенной полиадической системы однотактовой процедуре, определяемой выражением

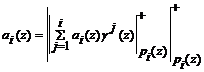,    (8)

где  i=1,2...,n количество оснований кода ПСКВ.

Обладая параллельно-конвейерной организации вычисления, данный алгоритм наиболее удачно реализуется на основе нейронных сетей.

Особенностью данного алгоритма является возможность вычисления коэффициентов ОПС на основе двухслойной нейронной сети за одну итерацию.

Для реализации алгоритма, базирующего на  выражении (8) потребуется в 1,15 раз меньше схемных затрат по сравнению с алгоритмом, представленным выражением (4) и более чем в 1,8 раза меньше по сравнению с методом рекурсивного перевода, определяемого выражением (3). При этом перевод из одной системы в другую производиться за одну итерацию, в то время как остальные алгоритмы затрачивают по n - итераций на каждую процедуру.

Можно отметить, применение коэффициентов обобщенной полиадической системы служит идеальной основой для построения отказоустойчивых вычислительных структур, функционирующих в системе классов вычетов [2,6].

Таким образом, применение разработанного метода перевода кодов из ПСКВ в ПСС позволяет повысить эффективность функционирования вычислительных устройств ЦОС, поднимая данные аппаратные средства на качественно более высокую ступень.

СПИСОК ЛИТЕРАТУРЫ

1. Акушский И.Я., Юдицкий Д.М. Машинная арифметика в остаточных классах. - М.: Сов. Радио, 1968. - 440 с.
2. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов /Нейрокомпьютеры: разработка, применение.№12, 2004, с.51-60.
3. Червяков Н.И. Преобразование цифровых позиционных и непозиционных кодов в системах управления и связи.- Ставрополь, СВВИУС.1985. - 63 с.
4. Червяков Н.И., Сахнюк П.А., Шапошников А.В., Ряднов С.А.Модулярные параллельные вычислительные структуры нейропроцессорных систем. М.: ФИЗМАТЛИТ,2003. - 288 с.
5. Элементы применения компьютерной математики и нейроинформатики/ Н.И. Червяков, И.А. Калмыков, В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; под редакцией Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216 с.
6. Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе класса вычетов. - М.: ФИЗМАТЛИТ, 2005. - 274.

Библиографическая ссылка