Существуют два основных направления повышения достоверности телеизмерений в задачах оперативного управления [1]:
- индивидуальная фильтрация каждого телеизмерения (ТИ) независимо от их остальной совокупности;
- использование связей между параметрами режима.
Первый случай применяется на начальном этапе обработки информации в ОИУК, и при этом могут быть ослаблены только определенные виды помех (наводимые помехи, линейные или нелинейные искажения сигнала).
Вторая часть методов базируется на статистических ( в частности, корреляционных) взаимосвязях между параметрами. В этом случае наиболее эффективным и мощным средством повышения достоверности ТИ является метод оценивания состояния ЭЭС.
Задача оценивания состояния заклюю-чается в определении установившегося (или переходного) режима по данным измерений и псевдоизмерений, содержащих погрешности и шумы, которые неизбежно присутствуют при передаче информации.
Для расчета режима необходимо иметь базисный набор параметров или вектор состояния, знание которого позволяет дорасчитать все остальные параметры режима.
Режим ЭЭС может быть описан уравнениями баланса активной и реактивной мощности в каждом из узлов сети:
![]() ;
;
![]() , (1)
, (1)
где Pнk, Pгk, Pk - активные мощности нагрузки, генерации и мощность, отдаваемая в сетьj-м узлом; Qнk, Qгk, Qk - то же для реактивных мощностей.
При этом уравнения балансов мощностей для k-го узла [2]:
![]() ;2
;2
![]() .3
.3
где U- модули напряжений в узлах;![]() ;
;![]() - активная и реактивная проводимости в узле k и ветви kj.
- активная и реактивная проводимости в узле k и ветви kj.
Для расчета установившегося режима в классической постановке вопроса необходимо иметь информацию о всех переменных Pi и Qi, кроме активной и реактивной мощностей балансирующего узла, а также одну фазу и один модуль напряжения.
Количество режимных параметров, входящих в уравнения1, 2 и 3, может значительно превышать число уравнений.
Остальные параметры режима обозначаются как вектор X =X(Y). Обозначив вектор телеизмерений как V¯ и действительные параметры как V , можно записать:
![]() ,
,
где nV - вектор ошибок измерений.
Задача оценивания состояния сводится к отысканию таких значений Y*, для которых вычисленные значения V(Y*) наиболее близки к измеренным значениям V¯.
При решении задачи потокораспределения возможны три варианта:
- вектор исходных данных образует базис;
- вектор исходных данных избыточен;
- исходных данных недостаточно для расчета режима.
При решении вопроса по оцениванию состояния с вероятностной постановкой задачи для ненаблюдаемых узлов рассматривается пример с вектором измеренных избыточных данных и производится расчет параметров трехузловой схемы, приведенной на рис. 1.
Рис.1 Расчетная схема
U1, δ P2,Q2
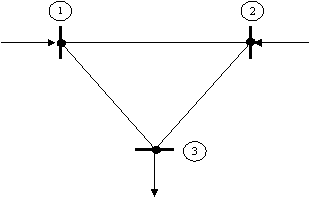
P3,Q3
В качестве вектора состояния используется полный набор измеренных параметров:
![]() ,δ1 - фазовый угол напряжения базового узла жестко задается равным нулю.
,δ1 - фазовый угол напряжения базового узла жестко задается равным нулю.
Для первого случая в качестве базиса из вектора состояния выбраны измеренные параметры ![]() . При этом составлена и решена система уравнений узловых напряжений в форме баланса мощностей методом Ньютона. Сравнительные результаты измеренных и расчетных параметров приведены в таблице 1.
. При этом составлена и решена система уравнений узловых напряжений в форме баланса мощностей методом Ньютона. Сравнительные результаты измеренных и расчетных параметров приведены в таблице 1.
Табл.1 Сравнительные результаты измеренных и расчетных параметров
|
|
P1 |
P 1-2 |
P 1-3 |
P 2 |
P 2-1 |
P 2-3 |
P3 |
P 3-1 |
P 3-2 |
|
Pизм(мВт) |
58.2 |
-10.2 |
-49.3 |
12.7 |
9.9 |
-22.9 |
-72.5 |
49.9 |
23.3 |
|
Pрасч(мВар) |
59.994 |
-9.941 |
-50.053 |
12.7 |
9.933 |
-22.633 |
-72.5 |
49.889 |
22.611 |
|
|
Q1 |
Q 1-2 |
Q 1-3 |
Q 2 |
Q 2-1 |
Q 2-3 |
Q3 |
Q 3-1 |
Q 3-2 |
|
Qизм(мВт) |
7.5 |
-0.8 |
-6.9 |
8.3 |
0.7 |
-8.9 |
-15.1 |
6.4 |
9.1 |
|
Qрасч(мВар) |
7.403 |
-0.68 |
-6.723 |
8.3 |
0.663 |
-8.963 |
-15.1 |
6.305 |
8.795 |
|
|
U 1 |
δ 1 |
U 2 |
δ 2 |
U 3 |
δ 3 |
|
Uизм (кВ) |
119.4 |
0 |
119.5 |
- |
119 |
- |
|
Uрасч (кВ), расч (рад) |
119.4 |
0 |
119.294 |
-0.001699 |
118.889 |
-0.0078 |
В приведенном примере небалансы измеренных параметров для узлов составляют:
P1=2.23 %; Q1=2.6%; P2=1.31 %; Q2= 1.12%; P3=0.96 %; Q3= 2.64 %.
Как видно из таблицы 1, расчетные и измеренные значения имеют различия из-за погрешности измерительной системы сбора информации, которая в свою очередь зависит от класса точности измерительных трансформаторов и класса точности аналого-цифровых преобразователей (АЦП) устройств телемеханики.
При минимизации функции [3] ![]() (4)
(4)
рассчитывается режим линий с учетом погрешностей измерительного тракта,
где V¯- измеренные параметры;
V(x)- расчетные параметры;
R - диагональная матрица, содержащая на диагонали дисперсии ошибок соответствующих измерений.
Базис, как и в первом случае, принимается для расчета в классическом варианте: ![]()
Зная класс точности измерительных трансформаторов и АЦП, можно найти дисперсии ошибок измерений в случае нормального закона распределения: 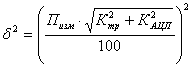 ,
,
где Пизм - значение измеренного параметра,
Ктр - класс точности измерительного трансформатора,
КАЦП - класс точности аналого-цифрового преобразователя.
В приведенном случае дисперсии ошибок измерений составили:
![]()
Тогда матрица весовых коэффициентов имеет вид:
 (7)
(7)
Матрица ![]() имеет вид:
имеет вид:
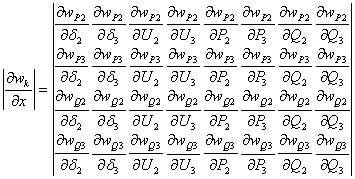 (8)
(8)
Приняв за фазовые углы напряжений в узлах ![]() и
и ![]() , необходимо произвести минимизацию функции 4:
, необходимо произвести минимизацию функции 4:
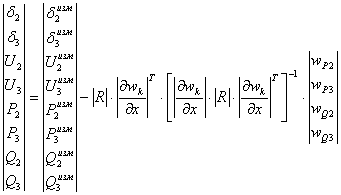 (9)
(9)
Путем подстановки полученных значений в уравнение 2 и 3 определяются невязки этих уравнений, и, если они больше порогового значения, производится вторая и следующие итерации расчетов.
После трех итераций значения расчета 1 приведены в сравнительной таблице 2.
Таблица 2. Сравнительная таблица измеренных и расчетных значений при учете погрешностей измерительного тракта
|
|
P1 |
P 1-2 |
P 1-3 |
P 2 |
P 2-1 |
P 2-3 |
P3 |
P 3-1 |
P 3-2 |
|
Pизм(мВт) |
58.2 |
-10.2 |
-49.3 |
12.7 |
9.9 |
-22.9 |
-72.5 |
49.9 |
23.3 |
|
Pрасч1(мВар) |
59.921 |
-9.921 |
-50 |
12.7 |
9.914 |
-22.614 |
-72.427 |
49.836 |
22.591 |
|
|
Q1 |
Q 1-2 |
Q 1-3 |
Q 2 |
Q 2-1 |
Q 2-3 |
Q3 |
Q 3-1 |
Q 3-2 |
|
Qизм(мВт) |
7.5 |
-0.8 |
-6.9 |
8.3 |
0.7 |
-8.9 |
-15.1 |
6.4 |
9.1 |
|
Qрасч1(мВар) |
7.401 |
-0.678 |
-6.723 |
8.3 |
0.66 |
-8.96 |
-15.098 |
6.305 |
8.793 |
|
|
U 1 |
δ 1 |
U 2 |
δ 2 |
U 3 |
δ 3 |
|
Uизм (кВ) |
119.4 |
0 |
119.5 |
- |
119 |
- |
|
Uрасч1 (кВ), δрасч (рад) |
119.4 |
0 |
119.294 |
-0.001699 |
118.889 |
-0.0078 |
В дальнейших расчетах в качестве базового режима рассматривается случай расчета 1, т.к. при этом соблюдается полный баланс, и здесь же учтены погрешности измерительной системы.
При предположении, что с узла 3 нет измерительной информации, задача расчета установившегося режима рассматривается в вероятностной постановке вопроса. При этом по заданному распределению исходных данных необходимо найти распределение вектора состояния, а по нему - распределение всех остальных параметров режима. В случае не наблюдаемости узла 3 необходимо иметь математическое ожидание ![]() и дисперсию
и дисперсию ![]() параметров P3 и Q3.
параметров P3 и Q3.
Из статистического анализа исходных данных за предыдущий период времени, учитывающий времена суток, математическое ожидание и дисперсия параметров 3-го узла определены как ![]() ;
;![]() ;
;![]() ;
;![]() .
.
Путем подстановки в уравнение 4 значений ![]() и
и ![]() получаются следующие результаты расчета 2, приведенные в таблице 3.
получаются следующие результаты расчета 2, приведенные в таблице 3.
Таблица 3. Сравнительная таблица измеренных и расчетных значений при расчете режима с вероятностной постановкой задачи для узла 3.
|
|
P1 |
P 1-2 |
P 1-3 |
P 2 |
P 2-1 |
P 2-3 |
P3 |
P 3-1 |
P 3-2 |
|
Pрасч1(мВар) |
59.921 |
-9.921 |
-50 |
12.7 |
9.914 |
-22.614 |
-72.427 |
49.836 |
22.591 |
|
Pрасч2(мВар) |
46.772 |
-6.398 |
-40.374 |
12.75 |
6.395 |
-19.145 |
-59.397 |
40.268 |
19.129 |
|
|
Q1 |
Q 1-2 |
Q 1-3 |
Q 2 |
Q 2-1 |
Q 2-3 |
Q3 |
Q 3-1 |
Q 3-2 |
|
Qрасч1(мВар) |
7.401 |
-0.678 |
-6.723 |
8.3 |
0.66 |
-8.96 |
-15.098 |
6.305 |
8.793 |
|
Qрасч2(мВар) |
5.304 |
0.239 |
-5.543 |
8.37 |
-0.246 |
-8.124 |
-13.272 |
5.271 |
8.001 |
|
|
U 1 |
δ 1 |
U 2 |
δ 2 |
U 3 |
δ 3 |
|
Uрасч1 (кВ), δрасч1 (рад) |
119.4 |
0 |
119.294 |
-0.001696 |
118.889 |
-0.00779 |
|
Uрасч2 (кВ), δрасч2 (рад) |
119.4 |
0 |
119.346 |
-0.001146 |
118.985 |
-0.006279 |
Большое расхождение расчетных и действительных параметров в табл.3 говорит о неприемлемости данного метода расчета для приведенной схемы.
Случай, когда вектор исходных данных избыточен по сравнению с базисом, приводит к переопределенной системе уравнений. Например, известны дополнительные параметры P23 и Q23 с имеющейся дисперсией ошибок измерения. В этом случае вектор состояния выглядит как
![]()
что позволяет дополнительно к уравнениям 2 и 3 добавить уравнения ;![]() ,
, ![]()
где P23, Q23, P31, Q31 - активная и реактивная мощности, вытекающие из узла в линию;
![]() - активные и реактивные потери мощности в линии,
- активные и реактивные потери мощности в линии,
![]() , где Rkj - активное сопротивление линии,
, где Rkj - активное сопротивление линии,
![]() , где Хkj - реактивное сопротивление линии.
, где Хkj - реактивное сопротивление линии.
Как известно, полная мощность, протекающая по линии в комплексной форме, выглядит [2]:
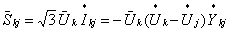 ,
,
где U¯k - комплексное число напряжения в узле k,
![]() - сопряженное комплексное число тока в линии kj,
- сопряженное комплексное число тока в линии kj,
![]() ,
,![]() ,
,![]() - сопряженные комплексные числа напряжений в узлах и проводимости линий kj.
- сопряженные комплексные числа напряжений в узлах и проводимости линий kj.
При разложении полной мощности на составляющие действительной и мнимой частей комплексного числа получается зависимость активной и реактивной мощностей от напряжений:
![]() ;
;
![]() ,
,
где ![]() - действительная составляющая напряжения узла,
- действительная составляющая напряжения узла,
![]() - мнимая составляющая напряжения узла,
- мнимая составляющая напряжения узла,
![]() - активная и реактивная проводимости линии.
- активная и реактивная проводимости линии.
На основе полученных уравнений, при минимизации функции 4, получается результат, приведенный в таблице 4.
Таблица 4. Сравнительная таблица расчетных значений при определении режима с избыточным вектором исходных данных и ненаблюдаемым узлом 3.
|
|
P1 |
P 1-2 |
P 1-3 |
P 2 |
P 2-1 |
P 2-3 |
P3 |
P 3-1 |
P 3-2 |
|
Pрасч1(мВар) |
59.921 |
-9.921 |
-50 |
12.7 |
9.914 |
-22.614 |
-72.427 |
49.836 |
22.591 |
|
Pрасч3(мВар) |
60.473 |
-10.081 |
-50.392 |
12.701 |
10.073 |
-22.774 |
-72.977 |
50.226 |
22.751 |
|
Kотн (%) |
0.9 |
1.6 |
0.78 |
0.008 |
1.6 |
0.44 |
0.76 |
0.86 |
0.71 |
|
|
Q1 |
Q 1-2 |
Q 1-3 |
Q 2 |
Q 2-1 |
Q 2-3 |
Q3 |
Q 3-1 |
Q 3-2 |
|
Qрасч1(мВар) |
7.401 |
-0.678 |
-6.723 |
8.3 |
0.66 |
-8.96 |
-15.098 |
6.305 |
8.793 |
|
Qрасч3(мВар) |
6.977 |
-0.577 |
-6.4 |
8.301 |
0.559 |
-8.86 |
-14.668 |
5.978 |
8.69 |
|
K (%) |
5.7 |
14.9 |
4.8 |
0.001 |
15.3 |
1.11 |
12.85 |
5.18 |
1.17 |
|
|
U 1 |
δ 1 |
U 2 |
δ 2 |
U 3 |
δ 3 |
|
Uрасч1 (кВ), δрасч1 (рад) |
119.4 |
0 |
119.294 |
-0.001696 |
118.889 |
-0.00779 |
|
Uрасч3 (кВ), δрасч3 (рад) |
119.4 |
0 |
119.295 |
-0.001732 |
118.892 |
-0.007876 |
|
K (%) |
- |
- |
0.0008 |
2.1 |
0.0025 |
1.1 |
Где K (%) - процентное соотношение разности величин между расчетным значением базового режима и расчета с вероятностной оценкой значений параметров третьего узла.
Анализируя результаты расчетов (табл.4), можно сделать вывод о приемлемости использованного алгоритма для определения режима энергосистемы в условиях вероятностной обработки данных нагрузок подстанций. Необходимыми условиями для применения этого алгоритма являются соблюдение баланса измеренных значений пограничных и основных узловых подстанций и наличие избыточного вектора исходных данных в наблюдаемых узлах.
СПИСОК ЛИТЕРАТУРЫ:
- Задачи оперативного и автоматического управления энергосистемами В.Г. Орнов, М.А. Рабинович. Москва. Энерго-атомиздат. 1988.
- Электрические сети и системы. В.И.Идельчик. Москва. Энергоатомиздат. 1989.
- Автоматизация диспетчерского управления в электроэнергетике. Под общей редакцией Ю.Н. Руденко и В.А. Семенова. Москва. 2000.
Работа представлена на научную конференцию с международным участием «Проблемы передачи и обработки информации» , 13-20 октября 2006г., ОАЭ. Поступила в редакцию 21.09.2006г.
Библиографическая ссылка
Ярцев С.Д. Оценивание состояния энергосистем с вероятностной постановкой задачи для ненаблюдаемых узлов // Современные наукоемкие технологии. 2006. № 8. С. 92-98;URL: https://top-technologies.ru/ru/article/view?id=24818 (дата обращения: 07.03.2026).



