Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы

Окунь А.С.

Налоговый потенциал страны в первую очередь зависит от налоговой базы - экономического положения предприятий, которые работают на данной территории и создают налоговую базу, являющуюся основной при установлении заданий регионам по мобилизации налогов и сборов в федеральный бюджет. Планирование величины налоговых поступлений осуществляется на базе анализа исполнения текущих налоговых обязательств, а также мониторинга и прогноза макроэкономической ситуации в стране в целом и в отдельных её регионах. Регулирование налоговой нагрузки возможно после анализа налогового потенциала регионов Российской Федерации, с разработкой методики определения возможной суммы поступления налогов и сборов.

Статья в формате PDF

144 KB

Планирование величины налоговых поступлений осуществляется на базе анализа исполнения текущих налоговых обязательств, а также мониторинга и прогноза макроэкономической ситуации в стране в целом и в отдельных её регионах.

Регулирование налоговой нагрузки возможно после анализа налогового потенциала регионов Российской Федерации, а также отдельных отраслей, включая естественные монополии, с разработкой методики определения возможной суммы поступления налогов и сборов. Более 50 % поступлений в федеральный бюджет приходится на 11 регионов и только 50 % - на остальные субъекты.

Различия между регионами по их роли в формировании налоговых доходов федерального бюджета объясняются рядом причин. Чем больше доля региона в ВВП страны, тем соответственно больше их доля в налоговых поступлениях в федеральный бюджет. Анализируя ситуацию можно сделать вывод, что увеличение темпов роста является следствием целенаправленной политики по увеличению налоговой нагрузки, и обусловлено изменениями в налоговом законодательстве. С отменой целого ряда налогов на 01.01.04г., а также понижением ставок (НДС с 20% до 18%, ЕСН с 35,6% до 26%) и порядка уплаты налогов, был пересмотрен перечень в сторону уменьшения по НДС, налогу на прибыль, имущество предприятий. Наблюдается значительное увеличение налоговой нагрузки по налогу на доходы физических лиц. В частности, увеличение ставки с 6% до 9% на доходы, полученным по дивидендам, введена с 01.01.02г. ставка 35% при определении налоговой базы при получении доходов в виде материальной выгоды, а также 13% при получении доходов в натуральной форме. Снижение ставки ЕСН на 9,6 пункта не решило поставленную задачу по увеличению поступлений от сбора данного налога. Работодателю даже в новых условиях не выгодно показывать доход работника полностью. Данная тенденция будет сохраняться до тех пор, пока работодатели будут являться налогоплательщиками данного налога, и сумма начисленного налога будет влиять на финансовый результат.

Таблица 1. Динамика налоговых поступлений

В консолидированный бюджет Российской Федерации в 2005г. поступило налогов, сборов и иных обязательных платежей, администрируемых ФНС России, (без учета единого социального налога, зачисляемого в федеральный бюджет) на сумму 4629,1 млрд. рублей, что в 1,4 раза больше, чем в 2004 году. В декабре 2005г. поступления в консолидированный бюджет составили 401,3 млрд. рублей и увеличились по сравнению с предыдущим месяцем на 1,7%.

Почти девять десятых всех доходов консолидированного бюджета сформированы за счет поступлений по пяти видам налогов. Основную часть налоговых и неналоговых доходов консолидированного бюджета в 2005г. обеспечили поступления налога на прибыль организаций - 28,8% и налога на добавленную стоимость на товары (работы, услуги), реализуемые на территории Российской Федерации - 22,2%.

В 2005г. в консолидированный бюджет Российской Федерации поступило федеральных налогов и сборов 4299,4 млрд. рублей (92,9% от общей суммы налоговых доходов), региональных - 198,7 млрд. рублей (4,3%), местных налогов и сборов - 56,4 млрд.рублей (1,2%), налогов со специальным налоговым режимом - 71,7 млрд.рублей (1,6%).

Поступление налога на прибыль организаций в консолидированный бюджет в 2005г. составило 1334,0 млрд. рублей, превысив значение показателя 2004г. в 1,5 раза. В 2005г. в консолидированный бюджет Российской Федерации (консолидированные бюджеты субъектов Российской Федерации) поступило 707,4 млрд. рублей налога на доходы физических лиц, что на 23,2% больше, чем в 2004г., в декабре 2005г. - 100,4 млрд. рублей, что в 1,7 раза больше, чем в ноябре 2005 года. Акцизов в по подакцизным товарам (продукции), производимым на территории Российской Федерации, поступило на сумму 236,1 млрд.рублей, что на 16,7% больше по сравнению с 2004г., за декабрь 2005г. - 19,2 млрд.рублей (на 4,8% больше, чем в ноябре 2005г.). Поступление налога на добычу полезных ископаемых составило 908,7 млрд.рублей, превысив уровень 2004г. в 1,8 раза, в декабре 2005г. - 84,2 млрд.рублей, или на 5,6% меньше, чем в ноябре 2005 года.

Проанализировав данные Госкомстата, Минфина (до 2003г МНС) РФ, можно сделать прогноз на среднесрочную перспективу роста динамики налоговой нагрузки, до 2007 года, и сделать объективные выводы по существующей на сегодняшний день бюджетной политике.

Временные ряды налоговых поступлений имеют преобладающую тенденцию. На основании этого можно построить тренд при помощи метода экстраполяции, при условии, что общие тенденции останутся без существенных изменений.

Для выбора вида кривой роста был использован метод характеристик приростов. Для этого исходный временной ряд  был сглажен методом простой скользящей средней, затем были проанализированы первые и вторые средние приросты, а также ряд произвольных величин, связанных с вычисленными приростами и сглаженными уровнями ряда:

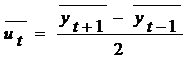
Ордината изменяется с постоянным темпом прироста, а отношение прироста к ординате является постоянной величиной.

В соответствии с характером изменения вычисленных показателей, выберем вид кривой роста для исходного временного ряда.

Первые, и вторые средние приросты изменяются линейно, логарифмы по приростам примерно одинаковы, а отношение прироста к ординате изменяется линейно, таким образом, возможны два вида кривой: либо полином третьего порядка, либо полином четвертого порядка.

Таблица 2. Показатели, определяющие вид кривой «роста налоговых поступлений в

федеральный бюджет РФ»

Рассмотрим полиномы третьей и четвертой степеней:

Параметры полученных кривых оценим при помощи пакета E-Views 3.0. Для полинома третьей степени получаем значение R-squared равное 0,9957, для полинома четвертой степени этот коэффициент имеет значение 0,9999.

Таким образом, можно сделать вывод, что рассматриваемая кривая роста имеет вид полинома четвертого порядка, данный вывод подтверждается сравнением последующих расчетов на точность и адекватность модели.

Коэффициенты были рассчитаны при помощи метода наименьших квадратов. Система уравнений принимает следующий вид:

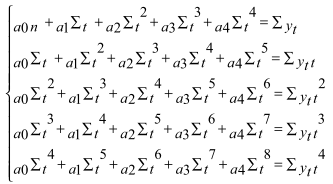
или

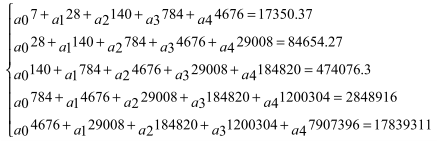
Получаем искомое уравнение:

Y = -364.8694084*А + 489.9583333*А2 - 114.770202*А3 + 8.973484848*А4+ 998.8571429, где:

Оценим адекватность и точность полученной трендовой модели.

Трендовая модель конкретного временного ряда считается адекватной, если правильно отражает систематические компоненты временного ряда. Это требование эквивалентно требованию, чтобы остаточная компонента ε = y_t - y_t (t = 1,2, ..., n) удовлетворяла свойствам случайной компоненты временного ряда:

• случайность колебаний уровней остаточной последовательности,
• соответствие распределения случайной компоненты нормальному закону распределения,
• равенство математического ожидания случайной компоненты нулю,
• независимость значений уровней случайной компоненты.

Проверим случайность колебаний уровней остаточной последовательности, т.е. подтвердим гипотезу о правильности выбора вида тренда. Для исследования случайности отклонений от тренда мы располагаем набором разностей:

Таким образом, получилась последовательность, состоящая из серии плюсов равная 2, и минусов равную 5. Обозначим протяженность самой длинной серии через Кmax, а общее число серий - через v. Полученную выборку можно признать случайной для 5%-ного уровня значимости, так как выполняются следующие условия:

Т.е. 4<6, а 5>1,6. Следовательно, гипотеза о случайном характере отклонений уровней временного ряда верна.

Проверим соответствие распределения случайной компоненты нормальному закону распределения. Для этого исследуем показатели асимметрии и эксцесса по формулам:

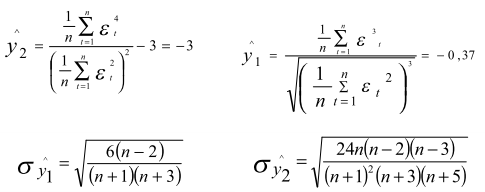
где y1 - выборочная характеристика асимметрии; y2 - выборочная характеристика эксцесса, а σ - соответствующие среднеквадратические ошибки.

Гипотеза о нормальном законе распределения случайной компоненты подтверждается, т.к. выполняются следующие неравенства:

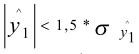            0,3779<0,9185

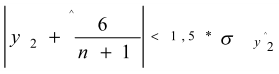              0,37<0,99

Далее проверим равенство математического ожидания случайной компоненты нулю, т.к. она распределена по нормальному закону распределения, проверка осуществляется на основе t - критерия Стьюдента.

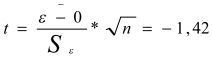
С учетом того, что расчетное значение этого критерия, меньше табличного (0,740697), с уровнем значимости - 0,05 и числом степеней свободы n-1 (т.е. число степеней свободы = 6), можно сделать вывод о том, что гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

Проверим независимость значений уровней случайной компоненты. Осуществим проверку отсутствия существенной автокорреляции в остаточной последовательности d-критерием Дарбина-Уотсона. Расчетное значение этого критерия равно:

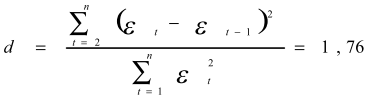
Сравнивая полученный критерий с критическими табличными значениями, которые для данной модели можно принять d1=0,61 и d2=1,4, мы видим, что расчетное значение критерия выше d2, из этого можно сделать вывод, что гипотеза об отсутствии существенной автокорреляции принимается полностью и дополнительные расчеты не требуются.

После проведения четырех проверок свойств остаточной последовательности, и получив по ним положительные результаты, можно сделать вывод об адекватности построенной трендовой модели.

Точность построенной модели оценим с помощью метода средней относительной ошибки аппроксимации:

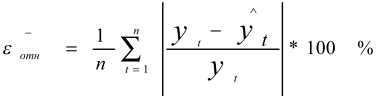
Получаем значение ошибки равное 0,4898 , т.е. менее 1%, что говорит о достаточно высоком уровне точности.

Построенная модель адекватна и достаточно точна, следовательно, ее можно принять за базу для построения прогноза на среднесрочную перспективу.

Очевидно, что точное совпадение фактических данных в будущем и прогностических точечных оценок маловероятно. Поэтому точечный прогноз должен сопровождаться двусторонними границами, т.е. указанием интервала значений, в котором с достаточной долей уверенности можно ожидать появления прогнозируемой величины.

Расчет доверительных интервалов при прогнозировании с использованием кривых роста опирается на выводы и формулы теории регрессий.

Методы, разработанные для статистических совокупностей, позволяют определить доверительный интервал, зависящий  от стандартной  ошибки оценки прогнозируемого показателя, от времени упреждения прогноза, от количества уровней во временном ряду и от уровня значимости (ошибки) прогноза.

Стандартная ошибка оценки прогнозируемого показателя, определяемая по формуле:

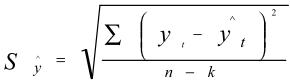
и принимает значение - 11,23.

Построим точечный прогноз на 2 шага вперед, т.е. на 2007 год, подставив соответствующее значение t в уравнение модели.

Вычислим значения доверительного интервала по следующей формуле:

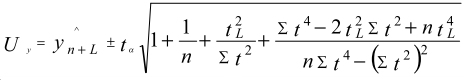
Исходя из этого, границы доверительного интервала принимают значения 12741и 12718.

Так как модель, на основе которой осуществлялся прогноз можно признать адекватной и достаточно точной, то с принятым уровнем значимости 0,05 т.е. с доверительной вероятностью 95% можно утверждать, что при сохранении налоговой политики без существенных изменений, прогнозируемая величина налоговых поступлений попадет в интервал, образованный нижней и верхней границами, т.е. они составят в среднем по точечному прогнозу 12730 млрд. руб.

Данная методика была использована в 2003г для построения прогноза динамики поступления налогов в консолидированный бюджет РФ. Согласно проведенных расчетов, налоговая нагрузка на 2005г. Составила 5402,79 млрд. руб. Фактически поступило налогов по данным Минфина РФ в 2005году - 4669,73 млрд. руб. Таким образом, отклонение составило 13,6%, которое объясняется изменением налогового законодательства:

• снижением ставки НДС на 2%, или 47,7 млрд. руб.
• снижением ставки ЕСН на 9,6% или 102,2 млрд. руб.

Кроме этого, расчет был произведен в условиях репрезентативной налоговой системы, т.е. при идеальном соблюдении налогового законодательство. Но на практике имеет место определенная доля налоговых правонарушений, основной причиной возникновения которых является неполное отражение или сокрытие объема производства продукции, налоговой базы и как следствие сумм налогов.

Таким образом, можно сделать вывод, о том, что предложенный метод построения прогнозов может применяться при анализе налогового потенциала, расчете налогового бремени и сокрытых объемов не только на макроэкономическом уровне, но и применительно к конкретному субъекту.

СПИСОК ЛИТЕРАТУРЫ:

1. Федосеева В.В. Экономико-математические методы и прикладные модели. - М.: Юнити, 2002 г., с189.
2. Кремер Н.Ш Высшая математика для экономистов. - М.: Юнити, 1997 г., с402.
3. Статистические сборники «Россия в цифрах», 1999-2003 гг.
4. Отчеты Минфина Российской Федерации об исполнении консолидированного и федерального бюджетов.

Библиографическая ссылка