Классифицировать адаптивные обучающие системы (АОС) можно по способу подборки очередной порции обучающей информации (ОИ): стохастические, навигационные и гибридные.
В стохастической модели состояние обучаемого на n-ом сеансе обучения описывается вектором вероятностей незнания каждого из элементов ОИ, а очередная порция учебного материала определяется вероятностью незнания ОИ. Этот тип моделей представлен АОС на основе итеративного научения. Итеративное научение (ИН) - многократное повторение обучаемой системой действий, попыток и т.д. для достижения фиксированной цели при постоянных внешних условиях [5]. Научение в общем случае - «процесс и результат приобретения индивидуального опыта» [4]. Постоянство внешних условий позволяет проводить количественное описание ИН в виде кривых научения, представляющих зависимость критерия уровня научения от времени или от числа итераций. В качестве результативной характеристики ИН принимается критерий уровня научения - временные, скоростные, точностные, информационные характеристики [1].
Скорость научения зависит от параметров модели: числа элементов, связей и законов их взаимодействия. Зная эту зависимость, можно предложить меры, приводящие к соответствующему изменению параметров модели и требуемого увеличения скорости научения [6]. Алгоритм обучения состоит в следующем.
- Осуществляется проверка знаний обучаемого.
- На основании проверки знаний обучаемого адаптируются параметры.
- Корректируется вектор незнания элементов обучающей информации.
- Вычисляется критерий качества обучения.
В зависимости от критерия качества обучения АОС решает: заканчивать обучение или по определенным правилам подбирать очередную порцию ОИ. На следующем цикле обучения снова повторяются пункты 1-5.
Примером использования итеративных обучающих моделей для создания АОС является обучение иностранной лексике. При изучении иностранного языка (например, английского) из-за пополнения словарного запаса в памяти генерируется множество ячеек для запомненных слов. Далее при актуализации i-го слова на русском языке в памяти возникают ассоциации с его английским значением Ai ,i=1,K,N. Ассоциативный параметр (степень связи i-го слова родного языка и его значения на иностранном языке) представляется следующим образом:
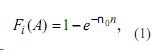
где -n0 — скорость восприятия информации обучаемым; n –число сеансов обучения;
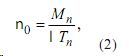
где Mn — объем очередной порции ОИ Un; Tn — продолжительность n-го сеанса обучения; 0<λ<1 — коэффициент потери информации во время ее поступления в память.
Состояние обучаемого на n-ом сеансе описывается вектором вероятностей незнания каждого из элементов обучающей информации:
![]()
где pi n — вероятность незнания i -го элемента в n-й момент времени tn. Вероятности незнания элементов ОИ изменяются по правилу
![]()
где a n i — скорость забывания i-го элемента ОИ на n-м сеансе обучения; t n i - время с момента последнего заучивания i -го элемента ОИ. Скорость забывания каждого элемента уменьшается, если этот элемент выдается обучаемому для запоминания, и не изменяется, если он не заучивается:
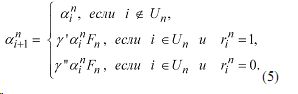
где a1i — начальное значение скорости забывания, оцениваемое методом максимального правдоподобия по выражению (6), a1i>0 (i =1,2,..,N), x - чсло незапомненных терминов из порции Un объемом Mn, впервые заучиваемых;
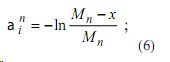
g´, g ′′ — параметры коррекции скоростей забывания, характеризующие индивидуальные особенности памяти обучаемого, оцениваемые методом максимального правдоподобия ![]()

Критерий качества обучения Qn для данной задачи определяется вероятностью незнания элемента ОИ, наугад выбранного из текста:
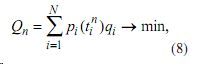
где pi (tni )- вероятность незнания i -го элемента ОИ; qi — относительная частота лексической единицы в частотном словаре текста (0< qi ).
Для минимизации значения Qn к концу сеанса обучения естественно в порцию ОИ включать элементы, имеющие наибольшее значение произведенияpi (tni ) qi, так как в результате их запоминания произведение становится равным нулю и тем самым наибольшим образом снижает значение Qn. Таким образом, для обеспечения оптимального значения Qn к концу n-го сеанса обучения необходимо найти Mn максимальных членов суммы в критерии, индексы которых и определят очередную порцию ОИ, выдаваемую ученику для запоминания [3].
Обучение заканчивается, когда Qn достигает требуемого уровня обученности δ, а число сеансов обучения n определяет продолжительность обучения. Таким образом, можно выделить следующие этапы алгоритма обучения:
Проверка знания обучаемым порции ОИ, в результате которой строится множество ответов обучаемого на тесты согласно выражению (7).
Осуществляется адаптация параметров модели обучаемого по правилу (5) с учетом выражений (1) и (2).
Корректируется вектор вероятностей незнания элементов ОИ, т.е. формируется Pn+1, согласно выражениям (4) и (5) и с учетом времени забывания информации после ее последнего заучивания tin:
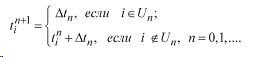
Вычисляется Qn+1 согласно выражению (8).
Если Qn+1 <= δ, то обучение заканчивается. При Qn+1 > δ определяется очередная порция ОИ Un+1, которая выдается для заучивания [3].
Навигационная модель обучаемого состоит из последовательности классов узлов, в каждом узле находится содержание, которое показывается обучаемым. Обучаемый может двигаться между узлами по связям. В каждом узле обучаемый может выбрать связи возврата к предыдущему узлу. Каждый узел идентифицируется номером и классом узла. У всех узлов есть навигационные правила.
Рассмотрим навигационную модель на примере. Каждому узлу сопоставляем символ, характеризующий его класс. Поня-тие класса необходимо для формализации навигационных правил и логического вывода на них. Класс также является одной из компонент модели обучаемого. Класс узла определяют следующие критерии:
- показывает ли АОС фрагмент контента, предназначенный только для определенного вида пользователя?
- предлагает ли узел пользователям объяснение, вопрос, тестовое задание или делает что-то еще в дидактическом плане?
- к каким из категорий контента АОС принадлежит узел (в случаях, когда информация узла может принадлежать более чем к одной категории)?
Навигационный метод основан на адаптивной технологии сокрытия связей. АОС, используя навигационное правило, решает, какие узлы скрывать и какие узлы могут быть связаны с текущим.
Обычно реализуются четыре вида навигационных правил: правила узла, общие правила, локальные пользовательские правила, глобальные пользовательские правила.
Пользовательское навигационным правило использует набор параметров обучаемого из его модели. Это правило может делиться на два типа: правило узла и общее правило. Правило узла определено и применяется только для определенного узла. Общее правило - для того чтобы описать наиболее часто встречающиеся навигационные пути в гиперпространстве.
В навигационном правиле разработчик АОС описывает связи, которые должны быть показаны в соответствии с идентификатором узла или в соответствии с классом узла, который является целью связи. Система скрывает все связи, на которые не ссылаются в навигационном правиле.
Если у узла есть несколько навигационных правил, система показывает все связи, которые подтверждаются любым навигационным правилом. Таким образом, если, по крайней мере, одно правило из нескольких правил одобряет показ определенной связи, система показывает связь независимо от других навигационных правил.
На рис. 1 показан пример навигации на основе всех описанных выше навигационных правил [1]. Классы определены следующим образом:
A - узлы с вопросом (тестовым заданием);
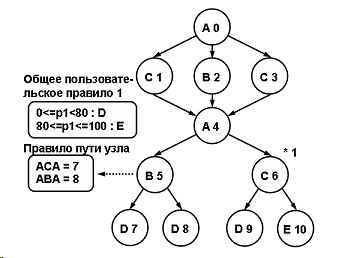
Рис. 1. Примеры навигационных правил [1]
B - узлы, содержащие информацию для правильного ответа обучаемого;
C - узлы с информацией для неправильного ответа обучаемого;
D - узлы с объяснением для студентов с высоким уровнем знаний;
E - узлы с объяснением для студентов с низким уровнем знаний.
Гибридная модель обучаемого объединяет в себе два предыдущих подхода, то есть выбор очередной порции ОИ зависит от вероятности незнания материала и от связей между блоками ОИ. рассмотрим конкретный пример, основой которого является байесовский подход. Учебный материал представлен вершинами графа (рис. 2), а отношения ребрами. Выделены 3 типа отношений: иерархические (потомок, предок), просмотровые (вперед, назад), семантические (ассоциативные). В соответствии с иерархическими отношениями структурным компонентам присваиваются индексы, которые используются для идентификации и адресации этих компонентов. На множестве одного иерархического уровня определяются отношения, служащие для описания порядка
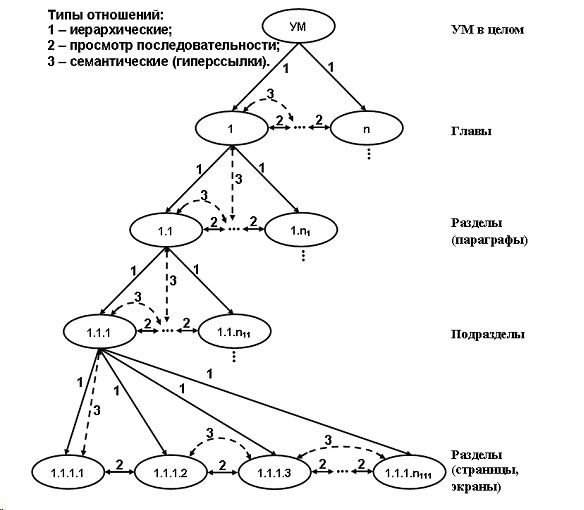
Рис. 2. Иерархическая декомпозиция учебного материала (УМ)[2]
предъявления их обучаемому. Эти отношения называются просмотровыми последовательностями. Семантические отношения связывают структурные компоненты, обладающие смысловой корреляцией. Эти отношения называются гиперсвязями [2].
Идентификация знаний обучаемого (определение значений Pj (k) осуществляется следующим образом. Для каждой операции yj вводится N гипотез Hi (i=1,2,...,N), соответствующих N состояниям обученности. Каждому i-му состоянию обученности соответствует условная вероятность P(Aj /Hj ) правильного применения операции yj в каждом из Lj ее применений, равная i/(N+1) Гипотезы Hi образуют полную группу несовместных событий, то есть имеет место:
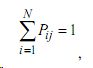
где Pij — вероятность гипотезы Hi для операции yj .
На каждом шаге обучения наблюдается событие Bj (k), состоящее в правильном применении j-ой операции Mj (k) раз из Lj (k) заданных. Эта информация служит для пересчета распределения вероятностей гипотез Pij с помощью формулы Байеса.
Каждый k-й шаг обучения характеризуется априорным и апостериорным распределениями вероятностей гипотез о состояниях обученности P0 ij (k) и P1 ij (k) , связанных между собой следующей зависимостью:
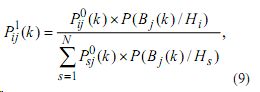
где P(Bj (k)/Hj ) — определяется по теореме Бернулли, то есть:
![]()
где ![]() - число сочетаний из Lj (k) по Mj (k).
- число сочетаний из Lj (k) по Mj (k).
Учитывая, что априорное распределение вероятностей гипотез на k-м шаге совпадает с апостериорным распределением на (k–1)-м шаге, то есть имеет место P0ij(k)= P1ij(k-1), формулу (9) можно переписать в виде, который подчеркивает ее рекурсивный характер (учитывается вся история обучения), а именно:
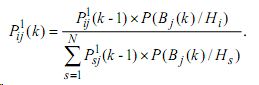
Вероятность правильного применения операции yj на k-м шаге определяется по формуле полной вероятности:
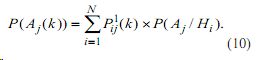
Окончательная оценка Pj (k) получается приведением значения, вычисленного по формуле (10), до введенных состояний обученности.
Осуществление на k-м шаге обучения контроля ошибок и выдачи необходимых объяснений позволяет вести прогнозирование вероятности правильного применения операций y на (k+1)-й шаг обучения:
![]()
где 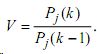
При вынесении решения о необходимости продолжения обучения модель определяет задание, адекватное знаниям обучаемого, на очередной шаг обучения, то есть обеспечивает индивидуальную минимизацию времени обучения.
Список литературы:
- Выродов А.П. Применение методов адаптивной гипермедиа при разработке автоматизированных обучающих систем / А.П. Выродов, Д.Б. Костарев, С.В. Ковалева, А.Н. Батрак // Вестник международного славянского университета. - Харьков, серия «Технические науки» том XI, №1, 2008.
- Галеев И.х. развитие адаптивных технологий обучения // Вестник ВГУ. - №4, 2004. - С. 76-83.
- Ковалев И.В., Карасева М.В., Суздалева Е.А. Системные аспекты организации и применения мультилингвистической адаптивно - обучающей технологии / Образовательные технологии и общество (Educational Technology & Society), №5. 2002. - C. 198-212.
- Краткий психологический словарь. - М.: ИПЛ, 1985, с. 201.
- Новиков Д.А. Закономерности итеративного научения. - М.: Институт проблем управления РАН, 1998. - 77 с.
- Растригин Л.А. Адаптивное обучение с моделью обучаемого. / Л.А. Растригин, М.Х. Эренштейн - Рига: Зинатне, 1988. -160 с.
Библиографическая ссылка
А .В. Топчиев, В. А .Чулюков МОДЕЛИ АДАПТИВНОГО ОБУЧЕНИЯ В КОМПЬЮТЕРНЫХ СИСТЕМАХ // Современные наукоемкие технологии. 2010. № 5. С. 62-68;URL: https://top-technologies.ru/ru/article/view?id=24747 (дата обращения: 14.02.2026).



