Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

Х. Гасадов Д.З.Алиев

В статье предлагается метод регуляризованной инверсии для определенного узкого класса задач атмосферных измерений. Показан пример применения предложенного метода для определения компонентов многокомпонентного континиума в среднем иК диапазона.

Статья в формате PDF

882 KB

регуляризация; дистанционное зондирование; инверсные задачи

атмосферные измерения; regularization; remote sensing; inverse tasks; atmosphere measurements

Такие задачи в некоторых случаях математически выражаются с помощью интегрального уравнения Фредгольма первого порядка, который имеет вид

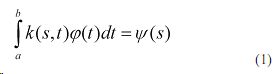
(1) где φ(t) - входное воздействие, подлежащее определению; ψ(S) - выходная реакция системы; k(S,t) - ядро преобразования.

Некорректность обратных задач типа (1) заключается в том, что если k(S,t) и - непрерывны по t, то решение (1), т.е. φ(t) может претерпеть значительные изменения при сколь угодно малых изменениях φ(t). Исходя от физической сути процесса, отображаемой уравнением (1), возможен случай возмущений не φ(t), а ядра преобразований k(S,t). При рассмотрении задач пассивного  зондирования атмосферы характерен именно первый случай, так как у исследователя атмосферы всегда имеется более - менее точная информация о k(S,t), функции поглощения j-й компоненты оптической плотности атмосферы. При этом φ(t) отражает общее количество выбранной компоненты в атмосфере.

Некорректность задачи (1) с позиции исследователя атмосферы может быть интерпретировано следующим образом. Получив информацию о приращениях s±∆s, а также имея приблизительную информации о φ(t), исследователь не сможет оценить возможности изменения k(S,t), с той же степенью приблизительности, если не принять специальных мер. При этом погрешность определения k(S,t) может быть намного выше, чем погрешность других исходных параметров. К таким специальным мерам следует отнести метод регуляризации А.Н. Тихонова, а также некоторые другие [1]. Следует отметить, что в настоящее время также известны нейросетевые способы решения данной задачи [2].

В настоящей статье рассматривается возможность использования нового метода регуляризации решения инверсных задач специфического класса, характеризующихся следующими свойствами:

1. Ядро интегрального преобразования (1) абсолютно невозмущаемо.
2. Входные воздействия изучаемого объекта имеют ограниченную возмущаемость т.е. они допускают применения к ним определенных ограничительных условий.

Предлагаемый метод предусматривает выполнение следующих шагов:

1) Дискретное представление S и t:

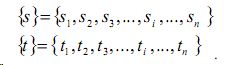
2) Запись уравнения Фредгольма в следующей дискретной форме

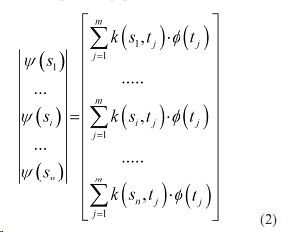
3)Поочередное умножение каждой i-й строки в (2) на регулировочный коэффициент d(S ), где i=1, n-1. При этом, i-я строка (i=1, n-1) в (2) будет иметь вид

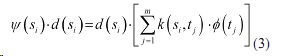
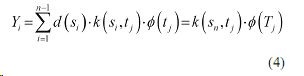
Очевидно, что коэффициенты d(si), i=1,n-1 могут быть вычислены путем решения системы уравнения (4) если n=m.

Если просуммировать выражение (3) по всем i=1,n-1 то с учетом (4) получим

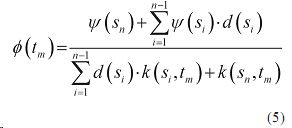
Таким образом, с учетом вышепринятых ограничений получена формула, позволяющая осуществить инверсию, т.е. по выходной реакции системы вычислять входное воздействие. При этом регуляризированность решения (5) очевидна, так как погрешность определения φ(t _m) согласно формуле (5) не будет превосходить среднюю погрешность определения ψ(S_i ).

Рассмотрим вопрос о применении вышеизложенного метода к задаче исследования многокомпонентного континуума в абсорбционной спектроскопии.

Прежде всего, поясним введенный здесь термин «многокомпонентный континуум» применительно к инфракрасной области спектра. Как известно [3], атмосферное континуальное поглощение, наблюдаемое в ИК спектральной области может быть разделено на газовый континуум и на континуум, вызванной жидкостными или твердыми микрочастицами. Физический причиной континуума N2 и O2 является абсорбция, вызванная столкновениями, однако континуальные линии поглощения H2 O и O2 появляются благодаря девиациям их линейных форм от обычно используемых форм линий из-за их расширения в результате столкновений. Стратосферный аэрозоль благодаря абсорбции и рассеянию может вызвать континуальный спектр радиации.

При этом рассеяние аэрозоля начинает вносить существенный вклад лишь при превышении радиуса аэрозольных частиц 1 мк.

Общий вид многокомпонентного континуума показан на рис. 1, где цифрами обозначены: 1- континуум O₂ ; 2 – континуум N₂ ; 3 – континуум H₂O; 4 – континуум O₂ ; 5 – континуум фонового аэрозоля; 6 – континуум вулканического аэрозоля.

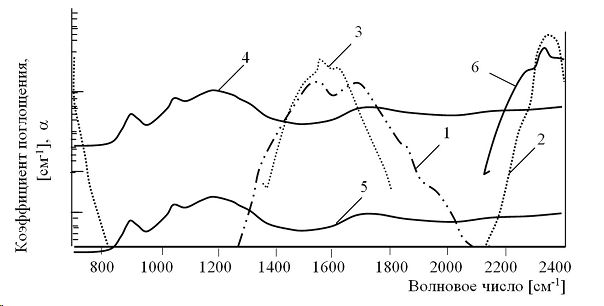
Рис. 1. Относительные значения коэффициентов поглощения для различных компонент в многокомпонентного континиума в среднем ИК диапазоне

Покажем, что при предлагаемом методе регуляризованной инверсии задача разделе- ния компонентов многокомпонентного континуума ИК диапазона может быть сведена к вышеуказанному решению задачи.

Закон Бугера – Бера для ближнего и среднего ИК-диапазона можно написать следующим образом:

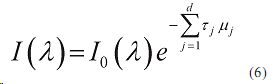
где I(λ) — величина измеренного сигнала на длине волны λ; I₀ (λ)- величина солнечной постоянной на длине волны λ; τ_j -оптическая плотность j-й компоненты; μ_j - оптическая масса.

В предлагаемом методе регуляризованной инверсии предполагается осуществление параллельных измерений на длинах волн λ_i ,i=1,n. Далее вводится безразмерная величина z_i определяемая как

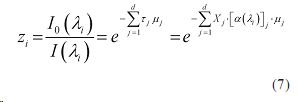
где X_j — общее содержание j-й компоненты многокомпонентного континуума; α(λ_j) — коэффициент поглощения этой компоненты.

Логарифмируя (7) получаем

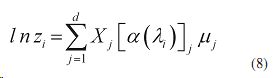
Рассмотрим параметр

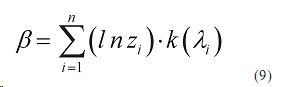
где k(λ_i ) — корректирующие коэффициенты.

С учетом (8) и (9) имеем:

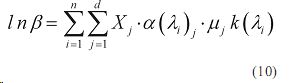
Примем условие d=n. Далее для упрощения записи принимаем, что μj=1, при j=1,d.

С учетом (9), выражение (10) представим в матричном виде.

Приняв k(λ_n )=1 для вычисления величин k(λ_i ),i=1,n–1 приравним суммы столбцов

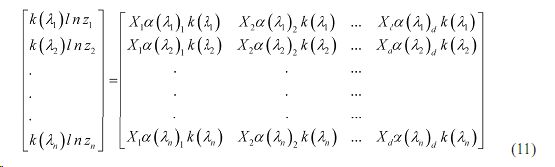
j=1,d–1 нулю. В результате получим систему линейных уравнений, решение которой дает искомые величины k(λ_i ),i=1,n–1.

С учетом вышесказанного, из (11) имеем

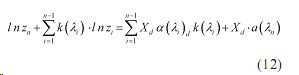
Из (12) находим

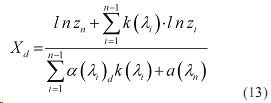
Как видно из (13) проведенная процедура инверсии дает регуляризированный результат, т.к. согласно (13) погрешность нахождения X_d не будет превышать среднюю погрешность определения z_i .

Таким образом, показано, что сужение рассматриваемого класса инверсных задач с учетом реальной специфики дистанционных атмосферных измерений позволяет осуществить регуляризованную инверсию, т.е. вычислить входные воздействия атмосферных объектов при нечетком задании их выходных реакций.

В заключение отметим, что предложенный метод регуляризации отличаясь своей простотой, предполагает использования определенного банка данных о корректирующих коэффициентах, которые могут быть вычислены заранее для различных атмосферных условий.

Список литературы

1. http://www.keldysh.ru/comma/html/ inverse/regular.html. Регуляризация
2. http://jre.cplire.ru/jre/dec01/7/text.html. А.В. Корженевский. Использование искусственных нейронных сетей для решения обратных задач электроимподансной и магнитоиндукционной томографии // Журнал радиоэлектроники, 2001, № 12.
3. Study of the Retrieval of Atmospheric Trace Gas Prof les from infrared spectra, Executive Summary. ESA Contract 12055/96/ NL/CN. esamultimedia.esa.int/does/gsp/completed/comp_sc_96_E20.pdf.

Библиографическая ссылка