Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова

С.Н. Абдуллаева

В статье показана возможность оптимизации процедуры аэрозольных измерений вблизи мощного источника аэрозольной эмиссии. решение вариационной оптимизационной задачи с ограничением, характеризующим точностные требования к серии измерений позволило получить аналитическое решение связывающее угол наблюдения Солнца в момент измерений с геометрическим расстоянием до источника.

Статья в формате PDF

1094 KB

экологические измерения; аэрозоль; загрязнение атмосферы; оптимизация; ecological measurements; aerosol; atmospheric pollution; optimization

Пожалуй, наиболее опасным для здоровья людей являются аэрозоли антропогенного происхождения, характеризующиеся малым эффективным диаметром аэрозольных частиц, которые обычно меньше 2,5 мкм. Именно такие мелкие частицы, долгое время находясь в подвешанном состоянии в воздухе легко вдыхаемы респираторной системой человека, что, в конечном счете, может привести к разрушению легких. Кроме этого, аэрозоли существенно влияют на климатический режим всей планеты, что представляет собой потенциальную опасность нежелательных климатических изменений при возникновении глобальных аэрозольных аномалий. Все это подчеркивает важность проведения аэрозольных измерений вблизи промышленных и природных объектов, являющихся мощным источником аэрозолей. В настоящей статье мы рассмотрим вопрос о проведении оптимальных аэрозольных измерений вблизи источника аэрозольной аномалии в атмосфере, прототипом котороВ настоящей статье ставиться задача оптимизации проведения аэрозольных измерений с точки наблюдения, передвигаемой на оси R. Ставятся следующие требования на цикл измерений по оси R:

1) Должны быть охвачены все точки кривой 1 или 2.

2) Суммарная интегрированная аэрозольная оптическая плотность за весь цикл из

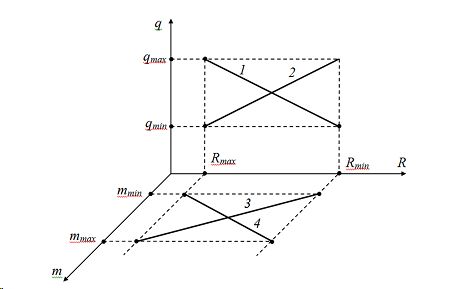
Рис. 1. Взаиморасположение функций q(R) (кривые 1, 2) и m(R) (кривые 3, 4) по отношению к R q - концентрация аэрозоля; m - оптическая масса; R - геометрическая координата

мерений по оси R не должна превышать заранее заданную величину.

3) Интегральная оценка

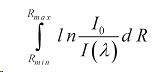
должна достичь наименьшей величины, где R_max — максимальная величина R;I₀ (λ) — величина Солнечной постоянной на длине волны λ;I(λ) — интенсивность излучения на уровне Земли.

Как известно, интенсивность солнечного излучения, прошедшего через атмосферу на уровне Земли может быть оценена по формуле Бугера [1]

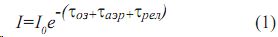
где τ_оз — оптическая толщина озона; τ_аэр —оптическая плотность аэрозоля; τ_рел — оптическая плотность релеевского рассеяния. Прологарифмировав выражение (1) имеем

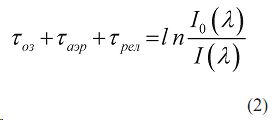
Далее учитываем, что релеевское рассеяние может быть рассмотрено в качестве систематической погрешности. Проинтегрировав выражение (2) по R (для упрощения выкладок считаем, что R_min =0) имеем

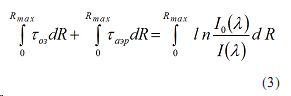
Отметим, что оптические толщины озона и аэрозоля, определяются как

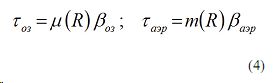
где β_оз — оптическая плотность озона; β_аэр — оптическая плотность аэрозоля; μ(R), m(R) — соответственно воздушные массы озона и аэрозоля.

На основании выражения (3) можно сформулировать две оптимизационные задачи оптимальных измерений аэрозолей.

Задача 1. Оптимизация измерения атмосферного аэрозоля вдоль трассы R. Для решения данной задачи должно быть установлено ограничительное требование к интегральной величине оптической толщины озона т.е.

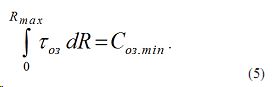
Известно [1], что при α>17º где α — угол наблюдения Солнца, имеет место фактическое равенство μ и m т.е. μ=m. С учетом этого рассматриваемая оптимизационная задача может быть сформулирована так: При ограничении (5) найти такую функцию m(R) при которой левая сторона выражения (3) достигает максимальное значение, т.е.

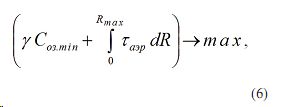
где γ - множитель лагранжа.

Задача 2. При ограничительном условии

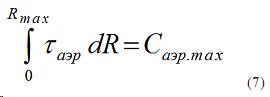
следует найти такую функцию m(R), кото- рая приводит левую сторону выражения (3) к минимальному значению, т.е.

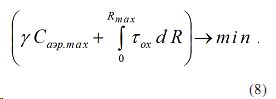
В настоящей статье мы подробно рассмотрим решение оптимизационной задачи 2.

Рассматриваемая далее задача оптимизации заключается в нахождении оптимальной функции m(R), приводящей левую сторону выражения (4) к минимальной величине при соблюдении ограничительного условия

Смысл условия (9) заключается в наложении ограничения на суммарную интегрированную аэрозольную оптическую плотность в проводимых измерениях. Таким образом, критерий оптимальности с учетом (3) и (9) может быть сформулирован следующим образом

где γ- множитель лагранжа. Для решения указанной оптимизационной задачи воспользуемся методом Эйлера.

Имеем

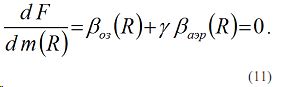
Из (11) имеем

С учетом (9) и (12) имеем

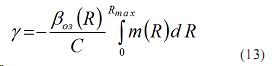
С учетом (13) в (11) имеем

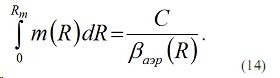
Из (14) имеем

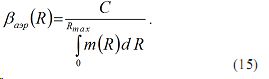
Учтя (15) в (11) имеем

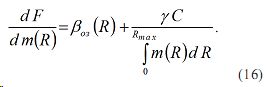
Из (16) имеем

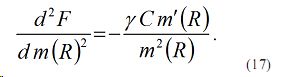
Проанализируем выражение (17). Для того, чтобы решение (14) было правильным, т.е. удовлетворяющим условию (8), с учетом отрицательной величины γ, следует потребовать условие неотрицательности m´(R), т.е. m´(R)>0. Таким образом, из полученного выражения (17) можно прийти к следующему заключению. Если измерительный сканирующий фотометр расположен вблизи точки с максимальной концентрацией аэрозоля, и его движение осуществляется в сторону минимальной концентрации, то величина m´(R) должно быть положительной и решение (14) вышерассмотренной оптимизационной задачи обеспечивает минимальную величину F. Из выражения (14) имеем

Таким образом, найдено аналитическое выражение для функциональной зависимости воздушной массы от геометрической координаты. Физически, режим оптимальных измерений должен быть осуществлен путем увеличения m по трассе R, что достигается путем изменения угла наблюдения.

Как указано в [2], решение полуэмпирического уравнения турбулентной диффузии для непрерывного точечного наземного источника аэрозоля может быть записано в виде

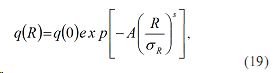
где q(0) — концентрация аэрозоля в точке R=0; A и σ- постоянные коэффициенты;σ_R- среднеквадратическое отклонение R. Известно [3], что оптическая плотность атмосферного аэрозоля может быть определена следующей эмпирической формулой

где B(λ=1 мкм)- коэффициент турбидности атмосферы; α — показатель Ангстрома.

 В рассматриваемом случае можно принять, что

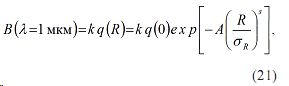
где k=const .

Тогда с учетом (21) и (21) имеем

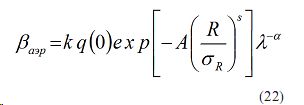
C учетом (22) и (18) имеем

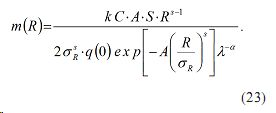
Таким образом, показано, что в рассматриваемой задаче оптимальных атмосферных измерений величина m(R) должно увеличиваться с увеличением R. Как видно из выражения (23) для точной физической реализации полученной функциональной взаимосвязи параметров m и R возможен вариант наличия некоторого временного интервала между фотометрическими измерениями под разным углом. Однако, такой временной интервал обычно не длится более 12–14 часов, в течение которой аномальная аэрозольная обстановка, созданная мощным источником мелкодисперсного аэрозоля вряд ли существенно изменится.

Таким образом, показано, возможность осуществления оптимальных аэрозольных измерений в непосредственной вблизи источника мелкодисперсного аэрозоля при априорном задании показателя точности всей серии измерений. Результаты полученные в данной работе могут быть использованы в экологических целях, при расчете и определении степени загрязненности атмосферы в производственных зонах.

Список литературы

1. Гущин Г.П., Виноградова Н.Н. Суммарный озон в атмосфере. Л., Гидрометеоиздат, 1988.
2. Бызова Н.Л., Гаргер Е.К., Иванов В.Н. Экспериментальные исследования атмосферной диффузии и расчеты примеси. Л., Гидрометеоиздат, 1991.
3. O’Neill N.T., T.F. Eck, B.N. Holben, A. Smirnov, O. Dubovik, and A. Royer (2001). Bimodal size distribution infuences on the variation of Angstrom derivatives in spectral and optical depth space // Journal Geophys. Res., 106 (D9), 9787–9806.

Библиографическая ссылка