Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы

Аткин И.С.

Статья в формате PDF

144 KB

                                                                (1)

Структурная схема ЧМ-дальномера представлена на рис.1 и состоит из частотного модулятора (1), СВЧ генератора (2), смесителя (3), фильтра низких частот (4), усредняющего счетчика, измеряющего частоту биений (5), передающей (6) и приемной (7) антенн.

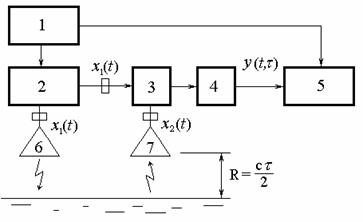
Рис. 1. Типовая структура ЧМ-дальномера

Непрерывный сигнал с генератора 2 излучается передающей антенной 6, поступая также на вход смесителя 3. При отражении излучаемого сигнала от поверхности, до которой измеряется расстояние, через приемную антенну 7 на вход смесителя 3 поступает сигнал x₂(t) = x₁(t -τ). В смесителе сигналы x₁(t) и x₂(t) перемножаются, а фильтр 4 выделит низкочастотный сигнал разностной частоты.

Для зондирующего сигнала  с законом изменения несущей частоты  ключевыми характеристиками модуляции будут закон модуляции F9t) (пилообразный или синусоидальный), девиация частоты (полоса качания) Δf и период модуляции T_M. Здесь где ‑ полная фаза колебания:

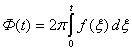                                 (2)

Сигнал биений  обрабатывается измерителем частоты 5, при этом полученное значение согласно (1) пропорционально дальности R. C учетом малости τ (при расстояниях до 100 м величина τ составляет ~10^-7сек.), используя теорему о среднем, для сигнала биений можно записать выражение:

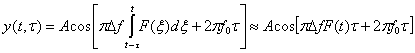                   (3)

Его мгновенная частота в любой момент времени запишется в виде: . Для симметричного пилообразного закона модуляции средняя за период модуляции Т_М частота биений составит:

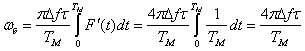
Аналогичное значение получается и для гармонического закона изменения частоты. Таким образом, частота биений составляет

.

С учетом , выражение для дальности имеет вид:

  (4)

Квазичастота (число переходов через ноль, совершенных сигналом биений за период модуляции) составит . Тогда выражение для дальности примет вид:

.

Дальномер с непрерывной частотной модуляцией будет точно измерять дальность лишь на конкретных расстояниях; в остальных случаях, будет иметь место методическая ошибка измерения ‑ т.н. «дискретная ошибка» [1], которая будет ограничивать точность измерения

 (5)

Очевидным способом уменьшения дискретной ошибки является увеличение полосы качания частоты Δf, однако по техническим причинам её редко делают больше 500 МГц. При этом дискретная ошибка составляет 15 см, что для некоторых задач неприемлемо.

В настоящей работе разработан метод дополнительной обработки сигнала биений, основанный на нелинейном полиномиальном преобразовании чебышевского типа. Полиномы Чебышева T_n(x), обладают следующим свойством [2]: если на вход нелинейного элемента, статическая характеристика которого представляет собой полином Чебышева степени n, подать сигнал вида cos[χ(t)] то на его выходе появится сигнал того же вида, но с аргументом увеличенным в n раз:

Тогда для нормированного по амплитуде сигнала биений (5) справедливо следующее преобразование:

,

что эквивалентно увеличению девиации частоты зондирующего сигнала, и как следствие, снижению дискретной ошибки n раз:

    (6)

Следует отметить, что максимально возможный порядок преобразования n будет зависеть от возможностей реализации нелинейного элемента чебышевского типа. Для аналоговой реализации элемента - n€[2;4], при цифровой реализации можно достичь существенных значений - n€[2;512], но только при высокой частоте дискретизации сигнала (15 МГц для n = 512 при Δf= 50 МГц = 1 мс).

Таким образом, данный метод позволяет асимптотически повышать точность ЧМ-дальномера, путем введения дополнительной обработки в низкочастотный тракт. Данный метод не имеет аналогов, так как после обработки мы получаем сигнал биений с искусственно увеличенной полосой качания, а частота сигнала может быть измерена любым существующим методом измерения частоты биений.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 08-07-00175-а и 10-07-97012-р).

СПИСОК ЛИТЕРАТУРЫ

1. Филькенштейн М.И. Основы радиолокации - М.: Радио и связь, 1983. ‑ 536с.
2. Корн Г., Корн Т. Справочник по математике. - М.: Наука, 1970. ‑ 831с.

Библиографическая ссылка